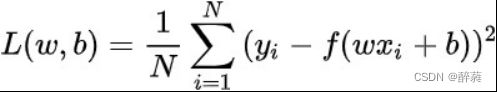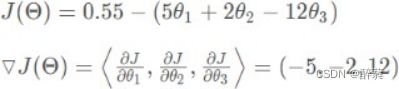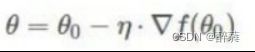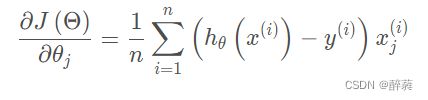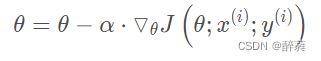梯度下降算法(Gradient descent)

一、 什么是梯度下降算法     

     首先，我们需要明确梯度下降就是求一个函数的最小值，对应的梯度上升就是求函数最大值。简而言之：梯度下降的目的就是求函数的极小值点，例如在最小化损失函数或是线性回归学习中都要用到梯度下降算法。

     ##梯度下降算法作为很多算法的一个关键环节，其重要意义是不言而喻的。

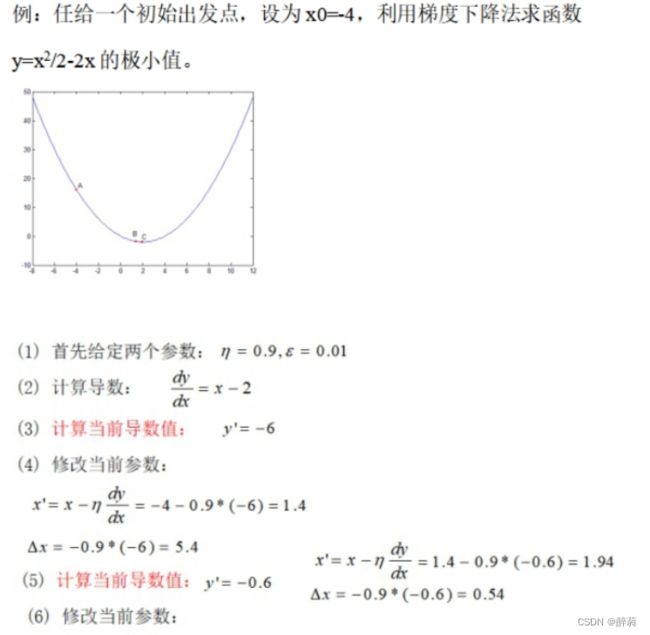
     梯度下降算法的思想：先任取点（x0,f(x0))，求f(x)在该点x0的导数f"(x0),在用x0减去导数值f"(x0),计算所得就是新的点x1。然后再用x1减去f"(x1)得x2…以此类推，循环多次，慢慢x值就无限接近极小值点。

      损失函数用来衡量机器学习模型的精确度。一般来说，损失函数的值越小，模型的精确度就越高。 如果要提高机器学习模型的精确度，就需要尽可能降低损失函数的值。而降低损失函数的值，我们 一般采用梯度下降这个方法。所以，梯度下降的目的，就是为了最小化损失函数。

我们设定场景来帮助理解：  

                              梯度下降法的基本思想可以类比为一个下山的过程。

 

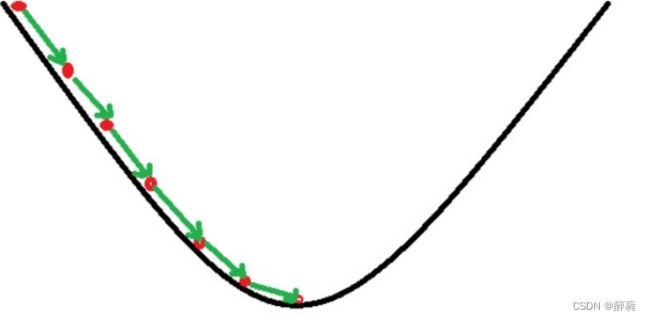
假设这样一个场景：一个人被困在山上（最左上），需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。怎么做呢，首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处。

    如上图，假如为山的纵切面，那每次下山一小步，经过N次后你便可以到达山底。

这类似于“走一步，看一步的想法”。在原有的位置上找到能到达的最低点，再以该点为起点继续寻找当前的最低点，以此往复，即可以到达最低处。当然，这样理解比较抽象，所以，下面我们给出数学概念。

二、数学解释

 

    梯度下降其实就是我们学习人工智能算法的一个基本算法，比如我们小学开始接触数学时候我们学习  加减乘除，最基本的算法 

1、梯度

    一阶函数里梯度就是表示某一函数在该点处的方向导数沿 着该方向取得较大值，即函数在*当前位置的导数*。如果函数为一元函数，梯度就是该函数的导数。

如果为二元函数，梯度定义为：

 

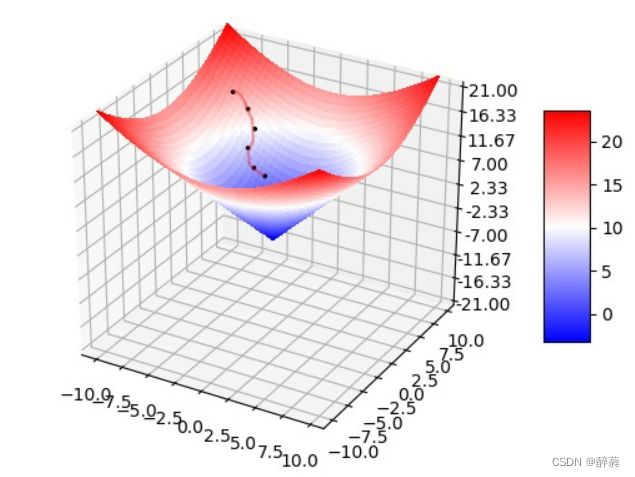
    我们可以看到，梯度就是分别对每个变量进行微分，然后用逗号分割开，梯度是用<>包括起来，说明梯度其实一个向量。向量有方向，梯度的方向就指出了函数在给定点的上升最快的  方向。

   再看刚才的例子，我们需要到达山底，就需要在每一步观测到此时最  陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度  的反方向就是函数在给定点下降最快的方向, 这正是我们所需要的 。所以我们只要沿着梯度的方向一直走，就能走到局部的最低点！
   

可以看出：单变量函数中，梯度代表的是图像斜率的变化，多变量函数中，梯度代表的是向量，变化最快的地方，即最陡峭的方向

 

2、核心公式

 

 3、步长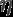（学习率）

 前面一直讨论如何下山最快和如何用数学方法来解决下山最快和下山的方向，那么还忽视了一个问题，就是下山的步子。

 我们可以通过来控制每一步走的距离，步长太大走的就容易偏离路线，其实就是不要走太快，错过了最低点。同时也要保证不要走的太慢，导致太阳下山了，还没有走到山下。所以的选择在梯度下降法中往往是很重要的！不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

小步长表现为计算量大，耗时长，但比较精准。

大步长，即较大的a aa，表现为震荡，容易错过最低点，计算量相对较小。

注意：由于函数凹凸性，对于凸函数能够无限逼近其最优解，对于非凸函数，只能获取局部最优解

4、梯度下降法的一般步骤

即：

1、给定待优化连续可微分的函数J（θ），学习率或步长，以及一组初始值（真实值）
2、计算待优化函数梯度
3、更新迭代
4、再次计算新的梯度
5、计算向量的模来判断是否需要终止循环
 

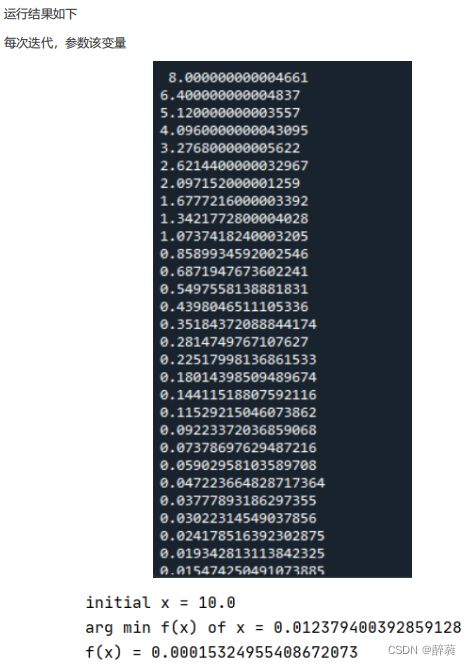
5、一元函数梯度下降实例

 

 代码段

#f(x)=x^2
import numpy as np
#定义原函数f(x)=x^2
def f(x):
    return np.power(x, 2)
#定义函数求导公式1
def d_f_1(x):
    return 2.0 * x
#定义函数求导公式2
def d_f_2(f, x, delta=1e-4):
    return (f(x+delta) - f(x-delta)) / (2 * delta)
xs = np.arange(-10, 11)# 限制自变量x的范围
plt.plot(xs, f(xs))#绘图
plt.show()
learning_rate = 0.1# 学习率（步长）
max_loop = 30# 迭代次数
x_init = 10.0# x初始值
x = x_init
lr = 0.01# ε值，不过我们下面用的是迭代次数限制
for i in range(max_loop):
    # d_f_x = d_f_1(x)
    d_f_x = d_f_2(f, x)
    x = x - learning_rate * d_f_x
    print(x)

    
print('initial x =', x_init)
print('arg min f(x) of x =', x)
print('f(x) =', f(x))

//能做，但不建议使用
#include "stdio.h"
 
double fun(double x){       //定义初始函数
    return x*x/2.0 - 2*x;
}
 
double der_fun(double x){       //求函数的导数
    return x - 2.0;
}
 
int main(){
    double length,accuracy;     //定义步长，精确度
    double x0,x1;      //定义初始位置
    printf("请输入步长,精确度及其初始位置：");
    scanf("%lf %lf %lf",&length,&accuracy,&x0);
    while(length*(-1)*der_fun(x0) > accuracy){
        x0 = x0 - length*der_fun(x0);
    }
    printf("x = %.5lf\ny = %.5lf",x0,fun(x0));
    return 0;
 
}

 6、批量梯度下降算法

前面所讨论中使用的梯度下降算法公式为：

可以看出，计算机会每次从所有数据中计算梯度，然后求平均值，作为一次迭代的梯度，对于高维数据，计算量相当大，因此，把这种梯度下降算法称之为批量梯度下降算法。

7、随机梯度下降算法 

随机梯度下降算法是利用批量梯度下降算法每次计算所有数据的缺点，随机抽取某个数据来计算梯度作为该次迭代的梯度，梯度计算公式：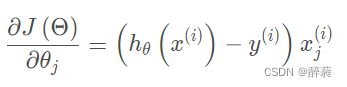

迭代公式可写为： 

由于随机选取某个点，省略了求和和求平均的过程，降低了计算复杂度，提升了计算速度，但由于随机选取的原因，存在较大的震荡性。