Sequence to sequence入门详解:从RNN, LSTM到Encoder-Decoder, Attention, transformer
文章目录
- 1. 前馈神经网络的缺点
- 2. 循环神经网络RNN
-
- 2.1. RNN的基本结构与数学定义
- 2.2. 输入输出长度的讨论
-
- 2.2.1. n x = n y = n n_x=n_y=n nx=ny=n
- 2.2.2. n x = n , n y = 1 n_x=n,n_y=1 nx=n,ny=1
- 2.2.3. n x = 1 , n y = n n_x=1,n_y=n nx=1,ny=n
- 2.2.4. n x = n , n y = m n_x=n,n_y=m nx=n,ny=m,Encoder-Decoder模型
- 3. RNN的复杂变种
-
- 3.1. GRU(Gated Recurrent Unit)
- 3.2. LSTM(Long Short-Term Memory)
-
- 3.2.1. peephole连接
- 3.2.2 projection
- 4. Encoder-Decoder模型
-
- 4.1. 几种典型的encoder-decoder
-
- 4.1.1. 第一种:语义编码C作为Decoder的初始输入
- 4.1.2. 第一种:语义编码C作为Decoder的每一步输入
- 4.2. Encoder-Decoder的缺点
- 5. Attention机制详解
-
- 5.1. attention机制中权重系数的计算过程
- 5.2. 几种典型的attention机制
-
- 5.2.1. 第一种:**Bahdanau Attention**
- 5.2.2. 第二种: **Luong Attention**
-
- 5.2.2.1. Global attention
- 5.2.2.2. Local Attention
- 5.2.3. **Self-Attention**
- 5.2.4. Multi-Headed Attention
- 6. 对输入序列进行位置编码
1. 前馈神经网络的缺点
对于输入向量中个分量的位置信息不感知,也即无法利用序列型输入特征向量中的位置信息(将个分量调换顺序最后训练出的模型是等价的),但是在实际的任务中,各分量是有先后关系的。例如,我们在理解一段文本时,孤立地理解每个字或者词是不够的,还要将它们作为一个整体的序列来理解。
2. 循环神经网络RNN
2.1. RNN的基本结构与数学定义
RNN的输入数据,一般有三个维度:batch大小,时间长度,特征维数。TensorFlow中的RNN层API的输入数据shape为[batch, timesteps, feature]。因为本节的图片来自Andrew NG的Coursera公开课中的例子,因此这里的RNN输入数据形状将以Andrew NG的习惯为例,这不影响原理的讲解。输入层的维数是 ( n x , m , T x ) (n_x,m,T_x) (nx,m,Tx),其中 n x n_x nx是每个训练样本的维数; m m m是一个batch的大小; T x T_x Tx是输入序列的长度。
输出层的维数是 ( n y , m , T y ) (n_y,m,T_y) (ny,m,Ty),其中 n y n_y ny是输出预测向量的维数; m m m是一个batch的大小; T y T_y Ty是输出序列的长度。
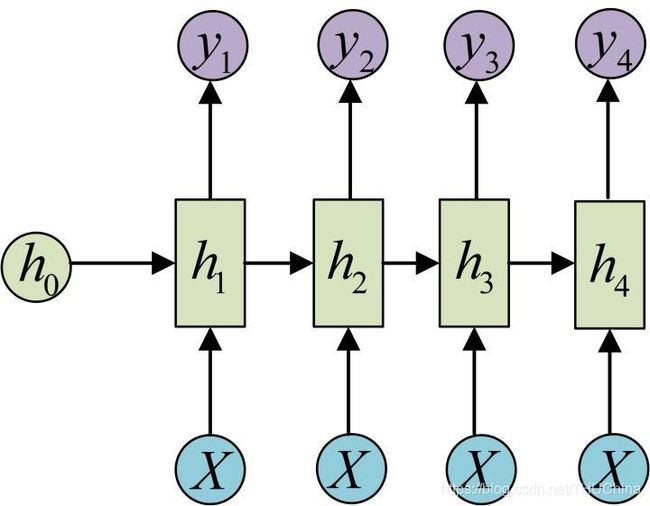
我们先研究输入向量和输出向量相等,即 n x = n y n_x=n_y nx=ny的情况,结构图如下所示(图片来源https://www.coursera.org/learn/nlp-sequence-models/notebook/X20PE/building-a-recurrent-neural-network-step-by-step)。
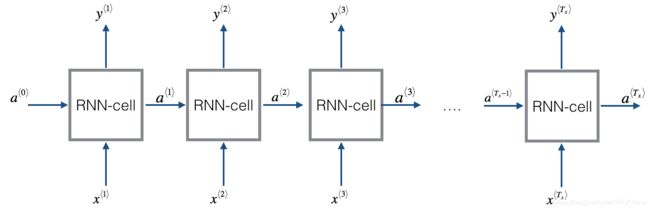
上下标说明举例: a 5 ( 2 ) [ 3 ] < 4 > a_5^{(2)[3]<4>} a5(2)[3]<4>表示第2个训练样本,第3层,第4个时刻,激活函数输出向量的第5维。
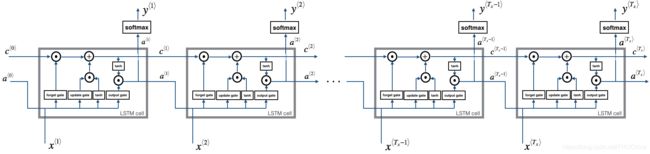
每个RNN-Cell的内部结构见下图
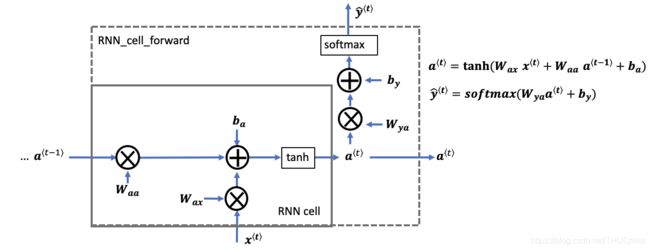
注意,输出 y ^ \hat y y^是状态向量 a a a经过线性变换再经过softmax变换得到的。
a ⟨ t ⟩ = t a n h ( W a x x ⟨ t ⟩ + W a a a ⟨ t − 1 ⟩ + b a ) y ^ ⟨ t ⟩ = s o f t m a x ( W y a a ⟨ t ⟩ + b y ) (2-1) \begin{aligned} a^{\langle t\rangle}&=tanh\left(W_{ax}x^{\langle t\rangle}+W_{aa}a^{\langle t-1\rangle}+b_a\right)\\ \hat y^{\langle t\rangle}&=softmax\left(W_{ya}a^{\langle t\rangle}+b_y\right)\\ \tag{2-1} \end{aligned} a⟨t⟩y^⟨t⟩=tanh(Waxx⟨t⟩+Waaa⟨t−1⟩+ba)=softmax(Wyaa⟨t⟩+by)(2-1)
需要注意的是,在不同的RNN-Cell中,上述公式里面的参数 W , b W,b W,b都是共享的。
2.2. 输入输出长度的讨论
2.2.1. n x = n y = n n_x=n_y=n nx=ny=n
第一种情况是输入输出长度相等的情况,如下图所示(图片来源https://www.jianshu.com/p/c5723c3bb921)

常用于序列标注模型,例如命名实体识别模型中。
2.2.2. n x = n , n y = 1 n_x=n,n_y=1 nx=n,ny=1
第二种情况是输入长度为N,输出长度为1(图片来源https://www.jianshu.com/p/c5723c3bb921)
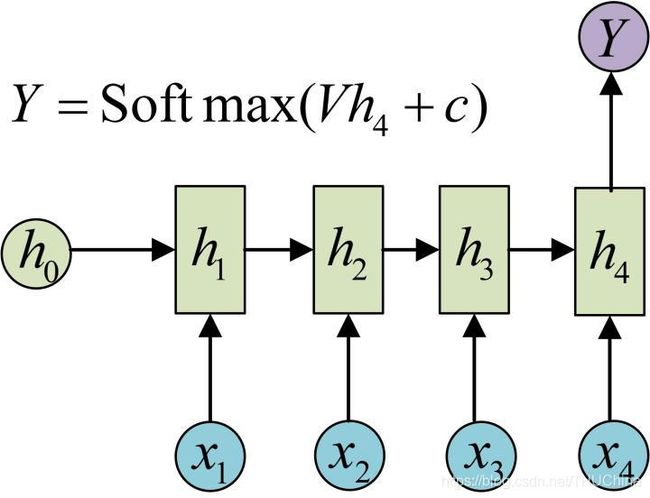
模型只在最后一个时刻输出,常用于文本分类模型
利用RNN网络预测sin函数的代码例子:https://github.com/lankuohsing/TensorFlow-Examples/blob/master/RNN/RNN_sin.py
2.2.3. n x = 1 , n y = n n_x=1,n_y=n nx=1,ny=n
第三种情况是输入长度为1,输出长度为N。uti实现时,可以将输入作为最开始时刻的输入,也可以作为所有时刻的输入(图片来源https://www.jianshu.com/p/c5723c3bb921)
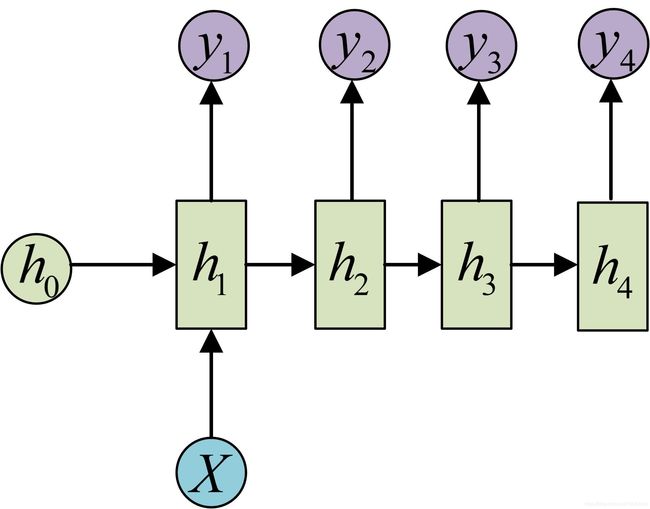
常用于文字生成模型中。
2.2.4. n x = n , n y = m n_x=n,n_y=m nx=n,ny=m,Encoder-Decoder模型
第四种情况是输入长度为N,输出长度为M的情况,也即Encoder-Decoder模型(图片来源https://www.jianshu.com/p/c5723c3bb921)
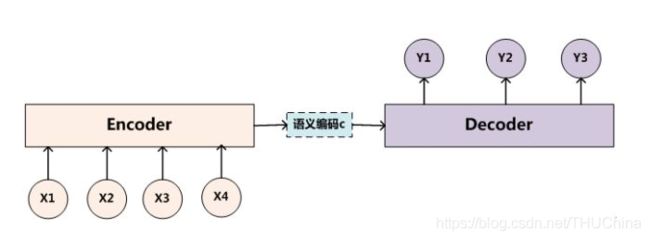
常用于语音识别、机器翻译等场景。在后面的章节中我们会详细介绍Encoder-Decoder模型
3. RNN的复杂变种
3.1. GRU(Gated Recurrent Unit)
GRU的提出是为了解决RNN难以学习到输入序列中的长距离信息的问题。
GRU引入一个新的变量——记忆单元,简称 C C C。 C ⟨ t ⟩ C^{\langle t\rangle} C⟨t⟩其实就是 a ⟨ t ⟩ a^{\langle t\rangle} a⟨t⟩
C C C的表达式不是一步到位的,首先定义 C C C的候选值 C ~ \tilde C C~:
C ~ ⟨ t ⟩ = t a n h ( W c [ C ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b c ) \tilde C^{\langle t\rangle}=tanh\left(W_c[C^{\langle t-1\rangle},x^{\langle t\rangle}]+b_c\right) C~⟨t⟩=tanh(Wc[C⟨t−1⟩,x⟨t⟩]+bc)
更新门:
Γ u = σ ( W u [ C ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b u ) \Gamma_u=\sigma\left(W_u[C^{\langle t-1\rangle},x^{\langle t\rangle}]+b_u\right) Γu=σ(Wu[C⟨t−1⟩,x⟨t⟩]+bu)
在实际训练好的网络中 Γ \Gamma Γ要么很接近1要么很接近0,对应着输入序列里面有些元素起作用有些元素不起作用。
C ⟨ t ⟩ = Γ u ∗ C ~ ⟨ t ⟩ + ( 1 − Γ u ) ∗ C ⟨ t − 1 ⟩ C^{\langle t\rangle}=\Gamma_u*\tilde C^{\langle t\rangle}+(1-\Gamma_u)* C^{\langle t-1\rangle} C⟨t⟩=Γu∗C~⟨t⟩+(1−Γu)∗C⟨t−1⟩
也即输入序列的有些元素,记忆单元不需要更新,有些元素需要更新。
The cat, which already ate …, was full
cat后面的词直到was之前,都不需要更新 C C C,直接等于cat对应的 C C C
可以解决梯度消失的问题.输出层的梯度可以传播到cat处
注: C C C和 Γ \Gamma Γ都可以是想聊,它们在相乘时采用的是element-wise的乘法。当为向量时,与cat的单复数无关的词对应的 Γ \Gamma Γ可能有些维度为零,有些维度不为零。为零的维度,是用来保留cat的单复数信息的;不为零的维度可能是保留其他语义信息的,比如是不是food呀之类的
目前讨论的是简化版的GRU,结构图如下
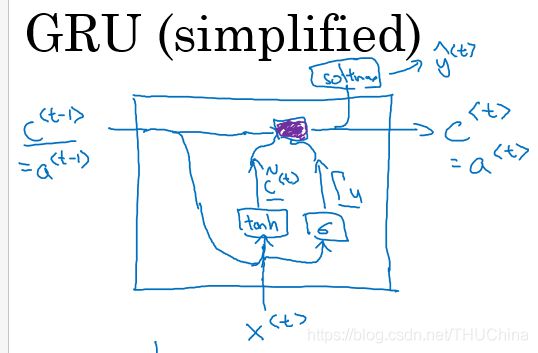
完整的GRU:
C ~ ⟨ t ⟩ = t a n h ( W c [ Γ r ∗ C ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b c ) Γ u = σ ( W u [ C ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b u ) Γ r = σ ( W r [ C ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b r ) C ⟨ t ⟩ = Γ u ∗ C ~ ⟨ t ⟩ + ( 1 − Γ u ) ∗ C ⟨ t − 1 ⟩ a ⟨ t ⟩ = C ⟨ t ⟩ (3-1) \begin{aligned} \tilde C^{\langle t\rangle}&=tanh\left(W_c[\Gamma_r*C^{\langle t-1\rangle},x^{\langle t\rangle}]+b_c\right)\\ \Gamma_u&=\sigma\left(W_u[C^{\langle t-1\rangle},x^{\langle t\rangle}]+b_u\right)\\ \Gamma_r&=\sigma\left(W_r[C^{\langle t-1\rangle},x^{\langle t\rangle}]+b_r\right)\\ C^{\langle t\rangle}&=\Gamma_u*\tilde C^{\langle t\rangle}+(1-\Gamma_u)* C^{\langle t-1\rangle}\\ a^{\langle t\rangle}&=C^{\langle t\rangle}\\ \tag{3-1} \end{aligned} C~⟨t⟩ΓuΓrC⟨t⟩a⟨t⟩=tanh(Wc[Γr∗C⟨t−1⟩,x⟨t⟩]+bc)=σ(Wu[C⟨t−1⟩,x⟨t⟩]+bu)=σ(Wr[C⟨t−1⟩,x⟨t⟩]+br)=Γu∗C~⟨t⟩+(1−Γu)∗C⟨t−1⟩=C⟨t⟩(3-1)
Γ r \Gamma_r Γr表示了 C ~ ⟨ t ⟩ \tilde C^{\langle t\rangle} C~⟨t⟩和 C ⟨ t − 1 ⟩ C^{\langle t-1\rangle} C⟨t−1⟩之间的相关程度
3.2. LSTM(Long Short-Term Memory)
没有了 Γ r \Gamma_r Γr,将 1 − Γ u 1-\Gamma_u 1−Γu用 Γ f \Gamma_f Γf代替
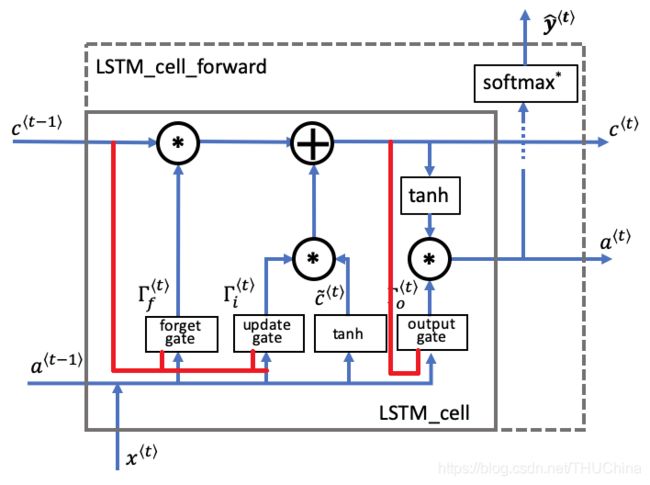
C ~ ⟨ t ⟩ = t a n h ( W c [ a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b c ) Γ u = σ ( W u [ a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b u ) Γ f = σ ( W f [ a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b f ) Γ o = σ ( W o [ a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b o ) C ⟨ t ⟩ = Γ u ∗ C ~ ⟨ t ⟩ + Γ f ∗ C ⟨ t − 1 ⟩ a ⟨ t ⟩ = Γ o ∗ t a n h ( C ⟨ t ⟩ ) y ~ ⟨ t ⟩ = s o f t m a x ( a ⟨ t ⟩ ) (3-2) \begin{aligned} \tilde C^{\langle t\rangle}&=tanh\left(W_c[a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_c\right)\\ \Gamma_u&=\sigma\left(W_u[a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_u\right)\\ \Gamma_f&=\sigma\left(W_f[a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_f\right)\\ \Gamma_o&=\sigma\left(W_o[a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_o\right)\\ C^{\langle t\rangle}&=\Gamma_u*\tilde C^{\langle t\rangle}+\Gamma_f* C^{\langle t-1\rangle}\\ a^{\langle t\rangle}&=\Gamma_o*tanh\left(C^{\langle t\rangle}\right)\\ \tilde y^{\langle t\rangle}&=softmax(a^{\langle t\rangle})\\ \tag{3-2} \end{aligned} C~⟨t⟩ΓuΓfΓoC⟨t⟩a⟨t⟩y~⟨t⟩=tanh(Wc[a⟨t−1⟩,x⟨t⟩]+bc)=σ(Wu[a⟨t−1⟩,x⟨t⟩]+bu)=σ(Wf[a⟨t−1⟩,x⟨t⟩]+bf)=σ(Wo[a⟨t−1⟩,x⟨t⟩]+bo)=Γu∗C~⟨t⟩+Γf∗C⟨t−1⟩=Γo∗tanh(C⟨t⟩)=softmax(a⟨t⟩)(3-2)
(注意公式里面的 Γ u \Gamma_u Γu等价于图片中的 Γ i \Gamma_i Γi)
3.2.1. peephole连接
C ~ ⟨ t ⟩ = t a n h ( W c [ a ⟨ t − 1 ⟩ , a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b c ) Γ u = σ ( W u [ c ⟨ t − 1 ⟩ , a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b u ) Γ f = σ ( W f [ c ⟨ t − 1 ⟩ , a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b f ) Γ o = σ ( W o [ c ⟨ t ⟩ , a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b o ) C ⟨ t ⟩ = Γ u ∗ C ~ ⟨ t ⟩ + Γ f ∗ C ⟨ t − 1 ⟩ a ⟨ t ⟩ = Γ o ∗ t a n h ( C ⟨ t ⟩ ) y ~ ⟨ t ⟩ = s o f t m a x ( a ⟨ t ⟩ ) (3-3) \begin{aligned} \tilde C^{\langle t\rangle}&=tanh\left(W_c[a^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_c\right)\\ \Gamma_u&=\sigma\left(W_u[c^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_u\right)\\ \Gamma_f&=\sigma\left(W_f[c^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_f\right)\\ \Gamma_o&=\sigma\left(W_o[c^{\langle t\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_o\right)\\ C^{\langle t\rangle}&=\Gamma_u*\tilde C^{\langle t\rangle}+\Gamma_f* C^{\langle t-1\rangle}\\ a^{\langle t\rangle}&=\Gamma_o*tanh\left(C^{\langle t\rangle}\right)\\ \tilde y^{\langle t\rangle}&=softmax(a^{\langle t\rangle})\\ \tag{3-3} \end{aligned} C~⟨t⟩ΓuΓfΓoC⟨t⟩a⟨t⟩y~⟨t⟩=tanh(Wc[a⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bc)=σ(Wu[c⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bu)=σ(Wf[c⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bf)=σ(Wo[c⟨t⟩,a⟨t−1⟩,x⟨t⟩]+bo)=Γu∗C~⟨t⟩+Γf∗C⟨t−1⟩=Γo∗tanh(C⟨t⟩)=softmax(a⟨t⟩)(3-3)
3.2.2 projection
对隐藏层状态a进行一次线性变换,降低其维数
C ~ ⟨ t ⟩ = t a n h ( W c [ a ⟨ t − 1 ⟩ , a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b c ) Γ u = σ ( W u [ c ⟨ t − 1 ⟩ , a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b u ) Γ f = σ ( W f [ c ⟨ t − 1 ⟩ , a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b f ) Γ o = σ ( W o [ c ⟨ t ⟩ , a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b o ) C ⟨ t ⟩ = Γ u ∗ C ~ ⟨ t ⟩ + Γ f ∗ C ⟨ t − 1 ⟩ a 0 ⟨ t ⟩ = Γ o ∗ t a n h ( C ⟨ t ⟩ ) a ⟨ t ⟩ = W p r o j a 0 ⟨ t ⟩ + b p r o j y ~ ⟨ t ⟩ = s o f t m a x ( a ⟨ t ⟩ ) (3-4) \begin{aligned} \tilde C^{\langle t\rangle}&=tanh\left(W_c[a^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_c\right)\\ \Gamma_u&=\sigma\left(W_u[c^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_u\right)\\ \Gamma_f&=\sigma\left(W_f[c^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_f\right)\\ \Gamma_o&=\sigma\left(W_o[c^{\langle t\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_o\right)\\ C^{\langle t\rangle}&=\Gamma_u*\tilde C^{\langle t\rangle}+\Gamma_f* C^{\langle t-1\rangle}\\ a_0^{\langle t\rangle}&=\Gamma_o*tanh\left(C^{\langle t\rangle}\right)\\ a^{\langle t\rangle}&=W_{proj}a_0^{\langle t\rangle}+b_{proj}\\ \tilde y^{\langle t\rangle}&=softmax(a^{\langle t\rangle})\\ \tag{3-4} \end{aligned} C~⟨t⟩ΓuΓfΓoC⟨t⟩a0⟨t⟩a⟨t⟩y~⟨t⟩=tanh(Wc[a⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bc)=σ(Wu[c⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bu)=σ(Wf[c⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bf)=σ(Wo[c⟨t⟩,a⟨t−1⟩,x⟨t⟩]+bo)=Γu∗C~⟨t⟩+Γf∗C⟨t−1⟩=Γo∗tanh(C⟨t⟩)=Wproja0⟨t⟩+bproj=softmax(a⟨t⟩)(3-4)
4. Encoder-Decoder模型
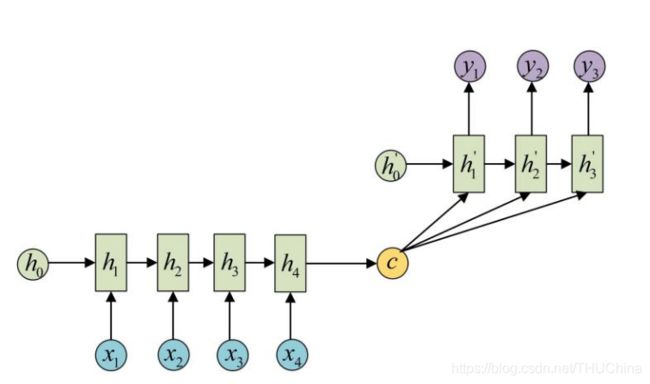
由前面的章节我们知道,Encoder-Decoder模型就是输入输出长度为一般情况的RNN模型,示意图如下:
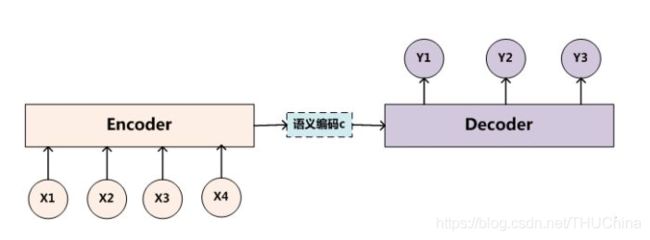
其中Encoder负责将输入进行编码,得到语义编码向量C;Decoder负责将语义编码向量C进行解码,得到输出。以机器翻译为例,英文作为输入,输出为中文。可以用如下的数学模型来表示:
i n p u t = ( x 1 , x 2 , ⋯ , x n ) C = f ( i n p u t ) y i = g ( C , y 1 , y 2 , ⋯ , y i − 1 ) , i = 1 , 2 , ⋯ , m o u t p u t = ( y 1 , y 2 , ⋯ , y m ) (4-1) \begin{aligned} input&= ( x_1,x_2,\cdots,x_n )\\ C&=f(input)\\ y_i&=g( C,y_1,y_2,\cdots,y_{i-1} ),i=1,2,\cdots,m\\ output&=( y_1,y_2,\cdots,y_m )\\ \tag{4-1} \end{aligned} inputCyioutput=(x1,x2,⋯,xn)=f(input)=g(C,y1,y2,⋯,yi−1),i=1,2,⋯,m=(y1,y2,⋯,ym)(4-1)
从Encoder得到C的方式有多种,可以将Encoder最后一个时刻的隐藏状态作为C,也可以将所有的隐藏状态进行某种变换得到C。
语义编码C在Decoder中的作用当时有多种,常见的有如下两种
(1) C作为Decoder的初始状态 h 0 h_0 h0。
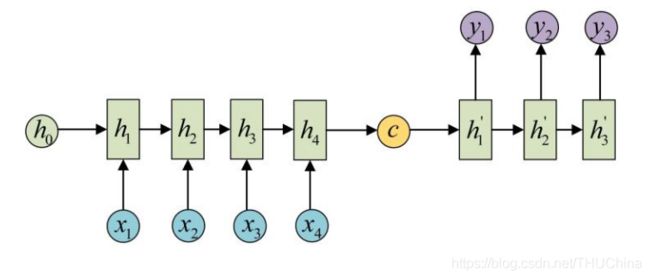
4.1. 几种典型的encoder-decoder
4.1.1. 第一种:语义编码C作为Decoder的初始输入
本小节的encode-decoder模型可以看成是seq2seq的开山之作,来源于google的论文https://arxiv.org/abs/1409.3215 Sequence to Sequence Learning with Neural Networks。该论文的模型是为了翻译问题而提出的,其中的encoder和decoder都采用LSTM,decoder中采用了beam search来提升效果。此外,该论文还采用了一个tric——将输入源句子倒序输入。这是因为,无论RNN还是LSTM,其实都是有偏的,即顺序越靠后的单词最终占据的信息量越大。如果源句子是正序的话,则采用的是最后一个词对应的state来作为decoder的输入来预测第一个词。这样是是不符合直觉的,因为没有对齐。将源句子倒序后,某种意义上实现了一定的对齐。
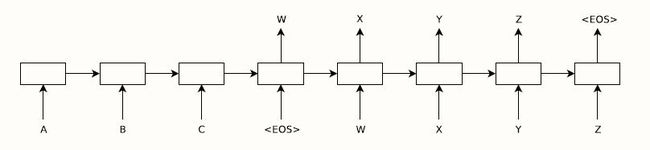
Encoder:
h t = t a n h ( W [ h t − 1 , x t ] + b ) c = h T (4-2) \begin{aligned} h_t&=tanh(W[h_{t-1},x_t]+b)\\ c&=h_T\\ \tag{4-2} \end{aligned} htc=tanh(W[ht−1,xt]+b)=hT(4-2)
Decoder:
h t = t a n h ( W [ h t − 1 , y t − 1 ] + b ) , h 0 = c o t = s o f t m a x ( V h t + d ) (4-3) \begin{aligned} h_t&=tanh(W[h_{t-1},y_{t-1}]+b),h_0=c\\ o_t&=softmax(Vh_t+d)\\ \tag{4-3} \end{aligned} htot=tanh(W[ht−1,yt−1]+b),h0=c=softmax(Vht+d)(4-3)
4.1.2. 第一种:语义编码C作为Decoder的每一步输入
https://arxiv.org/pdf/1406.1078 Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation
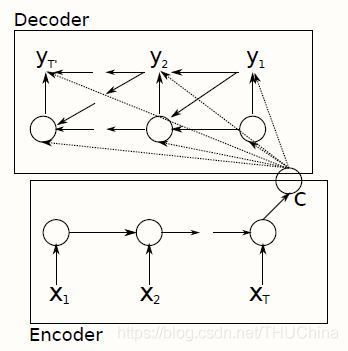
Encoder:
h t = t a n h ( W [ h t − 1 , x t ] + b ) c = ( V h T ) (4-4) \begin{aligned} h_t&=tanh(W[h_{t-1},x_t]+b)\\ c&=(Vh_T)\\ \tag{4-4} \end{aligned} htc=tanh(W[ht−1,xt]+b)=(VhT)(4-4)
Decoder:
h t = t a n h ( W [ h t − 1 , y t − 1 , c ] + b ) o t = s o f t m a x ( V h t + c ) (4-5) \begin{aligned} h_t&=tanh(W[h_{t-1},y_{t-1},c]+b)\\ o_t&=softmax(Vh_t+c)\\ \tag{4-5} \end{aligned} htot=tanh(W[ht−1,yt−1,c]+b)=softmax(Vht+c)(4-5)
4.2. Encoder-Decoder的缺点
- 对于输入序列的每个分量的重要程度没有区分,这和人的思考过程是不相符的,例如人在翻译的时候,对于某个一词多义的词,可能会结合上下文中某些关键词进行辅助判断。
- 如果在Decoder阶段,仅仅将C作为初始状态,随着时间往后推进,C的作用会越来越微弱。
事实上,Attention机制的提出,主要就是为了解决上述问题。
5. Attention机制详解
前面讲到,在一般形式的encoder-decoder中,输入信息先经过encoder编码保存在C中,C再被decoder使用。这种“直接粗暴”的方式,可能会导致输入信息没有被合理的利用,尤其是当输入信息过长的时候。为了解决这个问题,Attention机制被提出,解决的思路是:在decoder阶段,每个时间点输入的C是不同的(示意图如下图所示),需要根据当前时刻要输出的y去合理地选择输入x中的上下文信息。
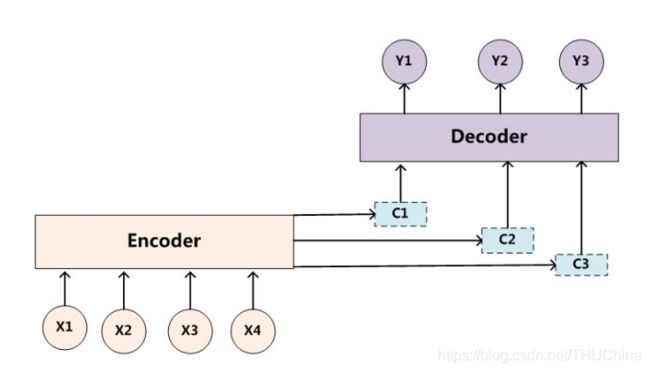
具体来讲,就是对encoder的隐藏状态进行加权求和,以便得到不同的C,以中文翻译英文为例,示意图如下:
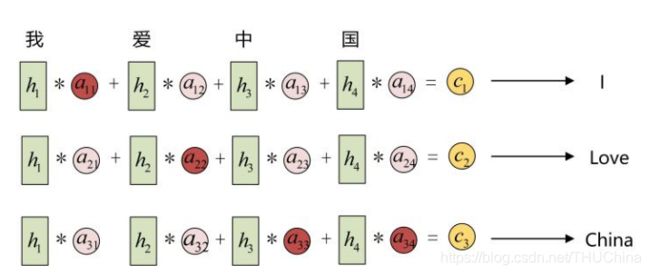
记 a i j a_{ij} aij为encoder中第 j j j个隐藏状态 h j h_j hj到decoder中第 i i i个隐藏状态 h i ′ h_i' hi′对应的 c i c_i ci的权重,可以通过训练确定的,具体计算方法见后文。attention机制的核心思想可以概括为"对输入信息加权求和得到编码信息c",也即如下公式:
c i = ∑ j = 1 n x a i j h j (5-1) c_i=\sum_{j=1}^{n_x}a_{ij}h_j\tag{5-1} ci=j=1∑nxaijhj(5-1)
5.1. attention机制中权重系数的计算过程
attention机制中权重系数有多种计算过程,对应于不同种类的attention机制。但是大部分的attention机制,都能表示为下文提到的三个抽象阶段。这里先引入几个概念。
我们将模型输入内容记为source,输出内容记为target。
source可以表示为一个一个的
通过计算Query和各个Key的相似性或者相关性(需要进行softmax归一化),得到每个Key对应Value的权重系数,然后对Value进行加权求和,即得到了最终的Attention数值。
A t t e n t i o n ( Q u e r y i , S o u r c e ) = ∑ j = 1 L x S i m i l a r i t y ( Q u e r y , k e y j ) ∗ v a l u e j (5-2) Attention(Query_i,Source)=\sum_{j=1}^{L_x}Similarity(Query,key_j)*value_j\tag{5-2} Attention(Queryi,Source)=j=1∑LxSimilarity(Query,keyj)∗valuej(5-2)
具体来说可以分为三个阶段,如下图所示:
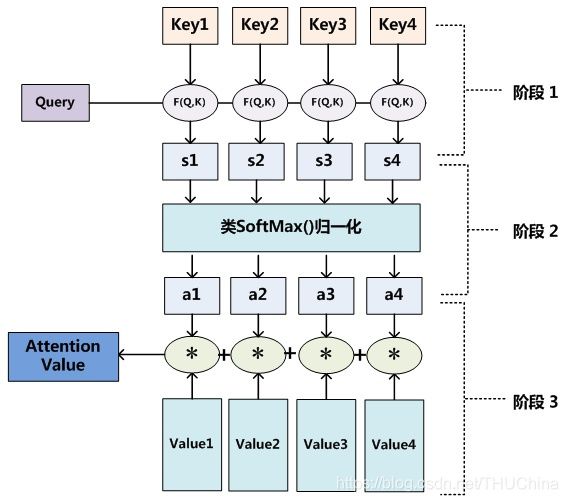
其中第一阶段计算相似性时有多种方法,例如向量点积、余弦相似度,甚至可以用一个小的神经网络来通过学习的方式计算。
第二阶段softmax归一化的公式如下:
a i j = s o f t m a x ( S i j ) = e x p ( S i m i j ) ∑ j = 1 L x e x p ( S i m i j ) (5-3) a_{ij}=softmax(S_{ij})=\frac{exp(Sim_{ij})}{\sum_{j=1}^{L_x}exp(Sim_{ij})}\tag{5-3} aij=softmax(Sij)=∑j=1Lxexp(Simij)exp(Simij)(5-3)
5.2. 几种典型的attention机制
5.2.1. 第一种:Bahdanau Attention
https://arxiv.org/abs/1409.0473 Neural Machine Translation by Jointly Learning to Align and Translate,这篇论文可以看做是attention机制的开山论文。该论文也是为了解决翻译问题而提出的模型,encoder采用了双向的RNN结构,正向RNN和反向RNN的每个时刻的隐藏state拼接成一个两倍长的新的state。如果要用一个简洁的公式来概括attention,那就是mlp + softmax+加权求和。之前的模型都是用一个固定长度的语义向量C来将encoder和decode连接起来,而这篇论文里是采用一个attention模型来连接。
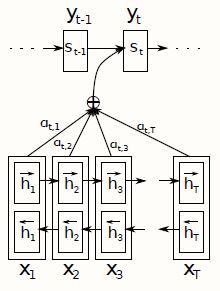
Encoder:
h i = t a n h ( W [ h i − 1 , x i ] + b ) (5-4) \begin{aligned} h_i&=tanh(W[h_{i-1},x_i]+b)\\ \tag{5-4} \end{aligned} hi=tanh(W[hi−1,xi]+b)(5-4)
语义向量:
e i j = a ( s i − 1 , h j ) α i j = e x p ( e i j ) ∑ k = 1 T x e x p ( e i k ) c i = ∑ j = 1 T x α i j h j (5-5) \begin{aligned} e_{ij}&=a(s_{i-1},h_j)\\ \alpha_{ij}&=\frac{exp(e_{ij})}{\sum_{k=1}^{T_x}exp(e_{ik})}\\ c_i&=\sum_{j=1}^{T_x}\alpha_{ij}h_j\\ \tag{5-5} \end{aligned} eijαijci=a(si−1,hj)=∑k=1Txexp(eik)exp(eij)=j=1∑Txαijhj(5-5)
其中 e i j e_{ij} eij是Encoder中 j j j时刻隐藏层状态 h j h_j hj对Decoder中 i i i时刻的处处状态 s i s_i si的影响程度; a ( s i − 1 , h j ) a(s_{i-1},h_j) a(si−1,hj)称为一个对齐模型,本论文中采用的是一个单隐藏层的多层感知机 a ( s i − 1 , h j ) = v a T t a n h ( W a s i − 1 + U a h i ) a(s_{i-1},h_j)=v_a^T tanh(W_a s_{i-1}+U_ah_i) a(si−1,hj)=vaTtanh(Wasi−1+Uahi),注意在实际推理的时候, U a h i U_ah_i Uahi是可以在推理之前预先算好的以减少推理计算量; α t i \alpha_{ti} αti是对 e t i e_{ti} eti进行softmax归一化成的概率,也即前文提到的 a i j a_{ij} aij或者叫attention权重; c t c_t ct是 t t t时刻的语义向量。可见上述计算得到权重系数 α i j \alpha_{ij} αij的的过程主要分为两步:MLP+SOFTMAX
Decoder:
s i = t a n h ( W [ s i − 1 , y i − 1 , c i ] ) o i = s o f t m a x ( V s i ) (5-6) \begin{aligned} s_i&=tanh(W[s_{i-1},y_{i-1},c_i])\\ o_i&=softmax(Vs_i)\\ \tag{5-6} \end{aligned} sioi=tanh(W[si−1,yi−1,ci])=softmax(Vsi)(5-6)
5.2.2. 第二种: Luong Attention
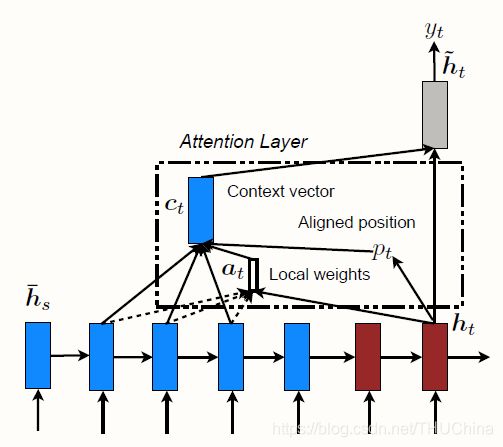
源自此论文https://arxiv.org/abs/1508.04025 Effective Approaches to Attention-based Neural Machine Translation。该论文提出了两种不同的attention:global attention和local attention。前者attention将作用在源句子的每个词,计算量较大;后者是出于减小计算量的考虑,只关注一个区间内的词(并且是在一个句子内部)。
5.2.2.1. Global attention
Encoder与上一小节中的不同之处在于,采用最顶层的LSTM的隐藏状态用于计算后续的语义向量C。
语义向量与上一小节的不同之处在于,在计算权重系数 α i j \alpha_{ij} αij的时候利用的是decoder中第 i i i个隐藏状态(上一小节是第 i − 1 i-1 i−1个)和encoder中第 j j j个隐藏状态来计算:
e i j = a ( s i , h j ) α i j = e x p ( e i j ) ∑ k = 1 T x e x p ( e i k ) c i = ∑ j = 1 T x α i j h j s i = t a n h ( W [ s i − 1 , y i − 1 ] ) \begin{aligned} e_{ij}&=a(s_{i},h_j)\\ \alpha_{ij}&=\frac{exp(e_{ij})}{\sum_{k=1}^{T_x}exp(e_{ik})}\\ c_i&=\sum_{j=1}^{T_x}\alpha_{ij}h_j\\ s_i&=tanh(W[s_{i-1},y_{i-1}])\\ \end{aligned} eijαijcisi=a(si,hj)=∑k=1Txexp(eik)exp(eij)=j=1∑Txαijhj=tanh(W[si−1,yi−1])
其中 a ( s i , h j ) a(s_{i},h_j) a(si,hj)的选择有多种:
a ( s i , h j ) = { s i T h j d o t s i T W a h j g e n e r a l v a T t a n h ( W a [ s i ; h j ] ) c o n c a t (5-7) a(s_{i},h_j)=\left\{ \begin{aligned} &s_i^Th_j &dot \\ &s_i^TW_a h_j &general\\ &v_a^Ttanh(W_a[s_i;h_j]) &concat \\ \end{aligned} \right. \tag{5-7} a(si,hj)=⎩ ⎨ ⎧siThjsiTWahjvaTtanh(Wa[si;hj])dotgeneralconcat(5-7)
Decoder:
s ~ i = t a n h ( W [ s i , c i ] ) o i = s o f t m a x ( V s ~ i ) (5-8) \begin{aligned} \tilde s_i&=tanh(W[s_i,c_i])\\ o_i&=softmax(V\tilde s_i)\\ \tag{5-8} \end{aligned} s~ioi=tanh(W[si,ci])=softmax(Vs~i)(5-8)
5.2.2.2. Local Attention
Global attention的缺点在于,预测某个target word时,需要计算该target对应的hidden state与encoder汇总所有hidden state之间的关系。当输入句子比较长时,这将非常耗时。Local attention就散为了解决这个问题,它只关注源句子中一个窗口内的词对应的hidden state。它的思想来源于soft-attention和hard-attention。
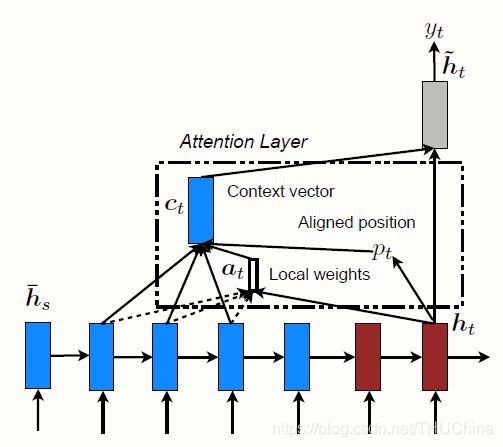
具体来说,对于要预测的某个target word, 首先计算出一个对齐位置 p j p_j pj,然后一个以 p i p_i pi为中心的窗口 [ p i − D , p i + D ] [p_i-D,p_i+D] [pi−D,pi+D]会被用来计算 c i c_i ci。窗口大小由经验给定。计算 c i c_i ci的方法与前面类似。
因此,重点在于如何计算 p i p_i pi。论文给出了两种方法:
- 单调对齐方式(Monotonic alignment):假设源句子和目标句子是单调对齐的。取 p i = i p_i=i pi=i。
- 预测对齐方式(Predictive alignment):采用如下公式计算 p i p_i pi:
p i = S ⋅ s i g m o i d ( v p T t a n h ( W p s i ) ) (5-9) p_i=S\cdot sigmoid(v_p^Ttanh(W_ps_i))\tag{5-9} pi=S⋅sigmoid(vpTtanh(Wpsi))(5-9)
其中S是源句子的长度。同时,为了增大 p i p_i pi附近的hidden state权重,权重系数将再乘上一个高斯分布:
a i j = α i j ⋅ e x p ( − ( j − p i ) 2 2 δ 2 ) (5-10) a_{ij}=\alpha_{ij}\cdot exp\left(-\frac{(j-p_i)^2}{2\delta^2}\right)\tag{5-10} aij=αij⋅exp(−2δ2(j−pi)2)(5-10)
其中 δ = D / 2 \delta=D/2 δ=D/2。 p i p_i pi是个实数,而j是个整数
5.2.3. Self-Attention
参考https://jalammar.github.io/illustrated-transformer/
Self-Attention最著名的应用是在论文https://arxiv.org/abs/1706.03762 Attention Is All You Need中,作为transformer结构的一个重要组成部分。
前面提到的几种attention,都是应用于基于RNN或者LSTM的encoder-decoder架构,通过计算decoder中隐藏状态和encoder中各个隐藏状态之间的关系来得到对应的权重。在《Attention Is All You Need》中,完全抛弃RNN/LSTM/CNN等结构,仅采用attention机制来进行机器翻译任务。并且在本论文中的attention机制采用的是self-attention,在encode源句子中一个词时,会计算这个词与源句子中其他词的相关性,减少了外部信息的依赖(这里我的理解是,与前面的几种attention机制不同,self-attention不需要decoder中的信息,也即encode一个句子时只用到了自身的信息,这就是self的含义)。
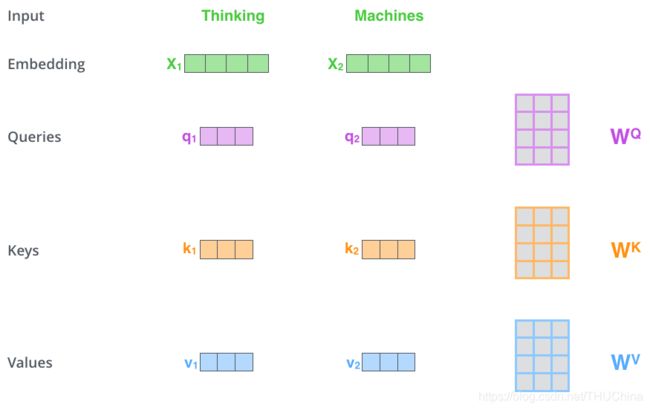
下面个详细讲解self-attention原理。第一阶段是计算三个vector(Q,K,V,它们的一个通俗理解见https://blog.csdn.net/qq_33431368/article/details/120212972),见下图:图片来源https://jalammar.github.io/illustrated-transformer/
为了简单起见,假设输入句子只有两个词,是"Thinking Machines"。如上图所示:首先得到这两个词的Embedding向量 x 1 , x 2 x_1,x_2 x1,x2(跟一般的nlp任务中的Embedding向量是一个概念),然后对于每个词,都计算出三个向量:Query Vector,Key Vector和Value Vector。计算过程为分别乘以三个矩阵: W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV。
第二阶段是计算attention分数,假设现在要计算的是"Thinking"的attention值,那么需要计算"Thinking"与该句子中所有词的分数。需要计算 s c o r e ( q 1 , k 1 ) , s c o r e ( q 1 , k 2 ) score(q_1,k_1),score(q_1,k_2) score(q1,k1),score(q1,k2)。常见是计算公式是内积。过程如下图所示:
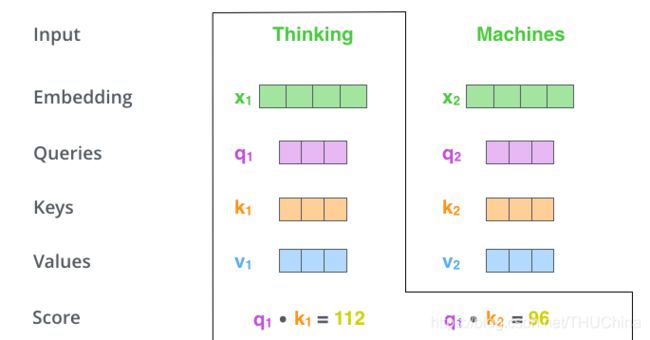
第三阶段是对分数进行归一化。首先除以 d k \sqrt d_k dk(Key Vector的维度),这是为了避免梯度爆炸;然后进行softmax归一化,这样是为了使得分数都在 [ 0 , 1 ] [0,1] [0,1]之间。
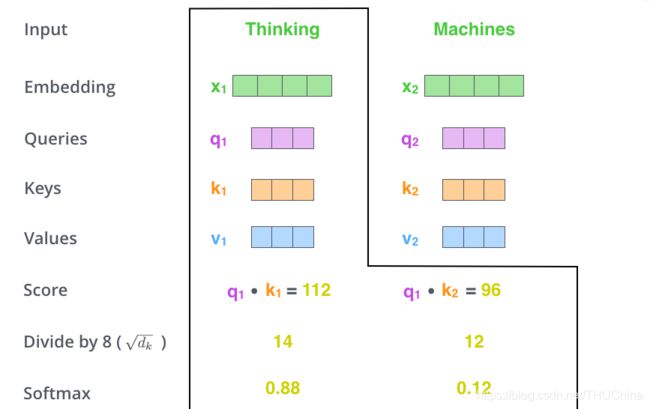
这个分数代表了encode "Thinking"需要放置多少注意力在各个单词上,不妨记为 s 1 i s_{1i} s1i。
第四阶段就是利用上述得到分数对所有的Value Vector加权求和得到"Thinking"的representation: z 1 = ∑ i = 1 L x s 1 i ∗ v i z_1=\sum_{i=1}^{L_x}s_{1i}*v_i z1=∑i=1Lxs1i∗vi
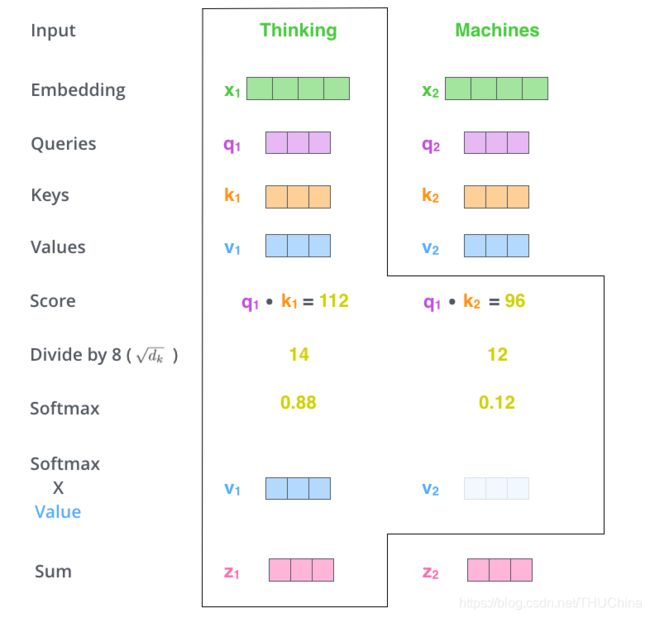
值得注意的是,上述过程是可以并行化计算的,这是self-attention相对于RNN,LSTM等序列模型的优势(在处理长序列问题上)。
最后,我们给出self-attention的紧凑表达式:
z = s o f t m a x ( Q ⋅ K d k ) V (5-11) z=softmax(\frac{Q\cdot K}{\sqrt {d_k}})V\tag{5-11} z=softmax(dkQ⋅K)V(5-11)
这样就一步到位得到了输入句子中所有词的represent vector。
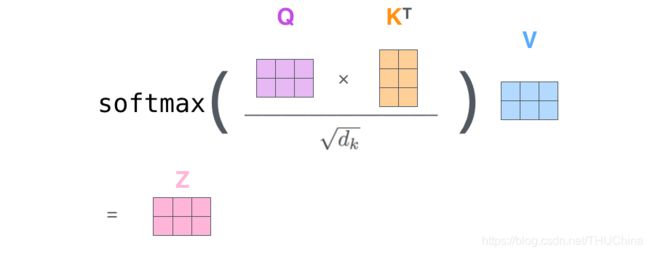
5.2.4. Multi-Headed Attention
所谓multi-headed attention,其实就是对输入Embedding做多次self-attention计算,每次都是在不同的子空间,可以学习到多份不同的权重参数(transformer里面是8份,也即8个head)对应不同的模式(类似于卷积里面的多个通道),然后将结果concat在一起。具体来讲这样做有两点好处:
- 这是为了增加模型对于其他位置的词的注意力能力。因为如果只是一个self-attention,很容易使得某个词的注意力大部分集中在它自身。
- 为attention层提供多个“表征子空间”。因为multi-headed attention有多个Q/K/V的矩阵集合(在transformer中有8个head),每个Q/K/V集合可以将输入的Embedding向量(或者上一个encoder-decoder)映射到不同的表征空间里。
如下图所示,输入Embedding得到8个head(对应8个分数z):
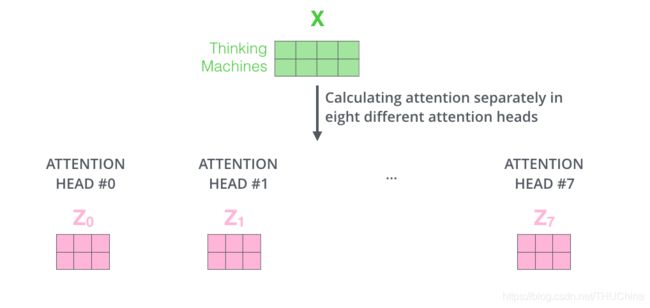
在进行后续计算时,一般会把这8个zconcat成一个长的矩阵,然后乘以一个矩阵 W O W^O WO,得到一个矩阵 Z Z Z,这个 Z Z Z捕获了前面8个z的信息。

6. 对输入序列进行位置编码
http://www.elecfans.com/d/1482740.html
https://www.zhihu.com/question/347678607
在经典的序列处理模型中,对于序列中各元素的“位置信息”的利用似乎都不太够。例如CNN只关注filter覆盖的区域中的局部位置信息;RNN能稍微关注到较长的信息,但是容易丢失更早期的信息;LSTM会挑出重点位置的信息,但由此可能造成丢失其他的位置信息;self attention/transformer中只关注全局位置信息,容易丢失相对位置信息。我们希望有一种模型既能捕获全局位置信息,又能捕获局部/相对位置信息。
对于序列问题,尤其是自然语言这种有强逻辑性的序列问题,显示地引入位置信息作为特征似乎显得格外重要。
例如,对于I believe I have fallen in love with you,如果采用self-attention,两个I的encoded输出将会是一样的。但是显然他们不一样。
那么如何引入位置信息呢?最朴素的想法是直接对位置进行整数编码:给定一个长度为 T T T的文本,位置编码 P E = p o s = 0 , 1 , 2 , ⋯ , T − 1 PE=pos=0,1,2,\cdots,T-1 PE=pos=0,1,2,⋯,T−1.这样的缺点在于,越往后面的元素,它的位置编码越大,可能会导致权重在它们身上的倾斜;它比其他的特征(例如input Embedding)大许多,会导致权重在位置编码特征倾斜太多。那对上述位置编码进行归一化呢? P E = p o s / ( T − 1 ) PE=pos/(T-1) PE=pos/(T−1)?这样只解决了数值过大的问题,但是它只关注绝对位置信息而丢失了相对位置信息。例如I like orange, because it provides me with VC和Since orange can provide me with VC, I like orange.其中两个like,按理说位置信息应该相差不大(它们在句中的绝对位置虽然不一样,但是相对位置是一样的),用上述编码是会出问题的。
简单总结一下位置编码的需求:
- 需要体现同一个单词在不同位置的区别;
- 需要体现一定的先后次序关系,并且在一定范围内的编码差异不应该依赖于文本长度,具有一定不变性。
- 需要值域落入一定数值区间内的编码,又需要保证编码大小与文本长度无关
一种选择就是周期函数,例如三角函数,这也是transformer中选用sin和cos函数来进行位置编码的原因。
在http://nlp.seas.harvard.edu/annotated-transformer/#positional-encoding 里面,采用的是如下公式:
P E ( p o s , 2 i ) = s i n ( p o s / 1000 0 2 i / d m o d e l ) P E ( p o s , 2 i + 1 ) = c o s ( p o s / 1000 0 2 i / d m o d e l ) PE_{(pos,2i)}=sin(pos/10000^{2i/d_{model}})\\ PE_{(pos,2i+1)}=cos(pos/10000^{2i/d_{model}}) PE(pos,2i)=sin(pos/100002i/dmodel)PE(pos,2i+1)=cos(pos/100002i/dmodel)
其中pos是位置,2i和2i+1分别代表偶数和奇数维度
如果将pos(元素在序列中的位置)作为横轴,画出上述三角函数曲线的话,三角函数的波长随着维度变化而变化,从 2 π 2\pi 2π按照几何级数变化到 2 ∗ 10000 π 2*10000\pi 2∗10000π,维度 2 ∗ i 2*i 2∗i和 2 ∗ i + 1 2*i+1 2∗i+1的波长是一样的, i = 0 , 1 , 2 , ⋯ , d m o d e l / 2 i=0,1,2,\cdots,d_{model}/2 i=0,1,2,⋯,dmodel/2