基于CNN的手写数字识别
基于CNN的手写数字识别
文章目录
- 基于CNN的手写数字识别
-
- 零、 写在之前
- 壹、 聊聊CNN
-
- 01. 什么是CNN
- 02. 为什么要有CNN
- 03. CNN模型
-
- 3.1 卷积层
- 3.2 池化层
- 3.3 全连接层
- 3.4 relu层
- 3.5 softmax层
- 贰、python的实践
-
- 01. 代码框架的构建
- 02. 准备工作
- 03. 数据处理
- 04. 卷积层正向传播
- 05. 池化层正向传播
- 06. softmax层正向传播
- 07. CNN模型
- 08. softmax层反馈
- 09. 池化层反馈
- 10.卷积层反馈
- 11. 动态绘图
- 12. 全部代码
- 叁、跑一跑模型
- 肆、调参以及思考
-
- 关于池化
- 关于卷积核大小
- 关于学习率
- 关于卷积核的个数
- 迭代次数
- 总结
咳咳,首先还是在之前简单的聊一下。在之前完成全连接神经网络之后竟然非常受欢迎,这是让我没有想到的。于是在我大喜的日子【生日】的时候,我决定把 CNN给徒手扒一扒。
这里说一下,本片博客参考了非常多的其他博客和非常少的论文,但因为我没有保存的习惯,所以看完就忘记人家放哪了…有点尴尬哈,所以这里集体感谢一下!
那废话不多说了,我们的卷积神经网络【CNN】即将启航!
零、 写在之前
按照惯例,我们依旧有关于阅读本篇博客的一些建议:
- 本篇博客有完整的代码复现,所以希望大家掌握好python的编程基础。【实话实说,很想拿C,但是望而却步】
- 本篇博客没有任何的框架,所用到的都属于python数据科学处理的基础知识,如有特殊函数会做出申明,所以不用担心。
- 还有就是你需要清楚什么是全连接神经网络,我们在这里是从全连接神经网络的区别出发的。
- 本篇博客会存在大量的实验,是基于神经网络完全建立完成之后的一些我好奇的地方的验证。
- 本篇博客很多观点仅代表我个人观点,管杀不管埋【我只是一个信息DOG,不是AI科班的】所以有错欢迎大家指正。
再有就是环境介绍了:
语言:python3.8.5
环境:jupyter
库文件:numpy | matplotlib
壹、 聊聊CNN
那么在最开始的地方我们先聊一聊关于CNN的一切吧。
01. 什么是CNN
卷积神经网络(Convolutional Neural Networks, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络(Feedforward Neural Networks),是深度学习(deep learning)的代表算法之一。对卷积神经网络的研究始于二十世纪80至90年代,时间延迟网络和LeNet-5是最早出现的卷积神经网络。 ——by《百度百科》
而如果要说正式进入公众视野,大量应用到深度学习上,还是从二十一世纪还是的。
02. 为什么要有CNN
如果有这个疑问,那么您已经在思考了,这是一个好消息。我们之前在做全连接神经网络的时候是不是只有三层?为什么是三层?隐藏层是在做什么的?如果您不知道为什么,或者您觉得这三个问题很有意思,请驻足在这里稍作思考…如果您心中有了想法,或者说您并不觉得这是什么问题,那么请继续往下看下去吧。
以下是我个人的一些拙见:
- 在之前的全连接神经网络中,我们对于图片的训练是将其转换成一维的数组去做运算的,但是人在做识别图像的时候可并不是这样的,因为这样将会丢失空间分布上的信息。
- 之前的全连接神经网络图片用的仅是28*28的图像,而现在的图片大小动辄都是百万像素起步,大小相差万倍。所以当图片打起来了以后他的参数将会非常夸张因为是全连接。
- 浅层的神经网络的识别率并不是非常理想,在我们之前的神经网络中可以看到,准确率大概只有88%左右。
而卷积神经网络可以非常有效的解决这些问题!
03. CNN模型
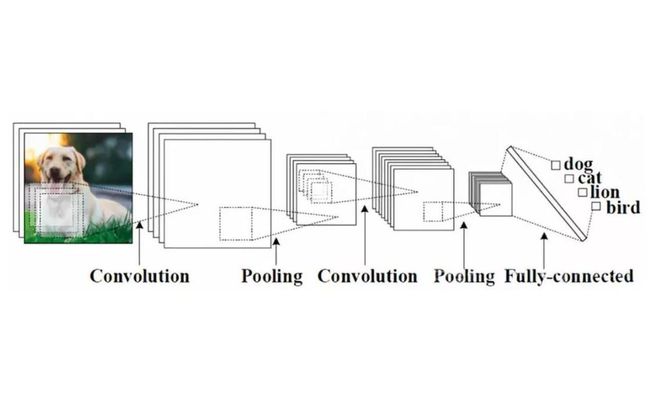
这里我们大致介绍一下CNN的模型有哪些部件,具体的讨论与实现会在后面代码中逐一展开。这里引入百度百科的图片:
3.1 卷积层
看名字就知道卷积层就是这个卷积神经网络的核心了。实际上确实如此,卷积层的参数由一组可学习的滤波器(filter)或内核(kernels)组成,它们具有一定的视野感受能力,可以对某一局部的数据有感知。在识别的过程中,每个滤波器对输入进行卷积,计算滤波器和输入之间的点积,并产生该滤波器的二维激活图。 简单来说,卷积层是用来对输入层进行卷积,提取更高层次的特征。
3.2 池化层
在卷积层中,我们把数据扩大了很多,这样对于数据的训练负担无疑是加重了。但是对于神经网络来说,数据的训练本身就是一件非常费时的事情,所以我们需要对数据量进行缩小且保留有用的信息,这就是池化的作用。
3.3 全连接层
和全连接神经网络相同,全连接层是用来将数据全部连接得到预测值。
3.4 relu层
relu层是我们神经元中的激活函数。
3.5 softmax层
softmax 的主要思想是为我们的神经网络定义一种新的输出层。也就是最终帮我们筛选出新的结果的一层。
想必大家对于以上的五个层有了大致的印象,但他们究竟是怎么样的,能有什么用呢?接下来让我们在实践的过程中在慢慢梳理。
贰、python的实践
01. 代码框架的构建
在本次最基础的框架中,我们将实现卷积层、池化层以及softmax层的构建,并完成对手写数据集的训练。
02. 准备工作
%matplotlib auto
在这次的训练过程中,我们将开启炫酷的动态损失函数图的展示,所以我们将调用Ipython的魔法,使展示的图片出现在新建窗口上。
import numpy as np
import matplotlib.pyplot as plt
03. 数据处理
咱这次的CNN识别中,我们依旧采用手写数字的数据集,训练集传送门, 测试集传送门。
那么我们现在就要对这些将数据读入了:
# 读入文件的地址,返回数据集的数据和标签
def read_data(path):
print("数据加载ing...")
data_file = open(path, 'r')
data_list = data_file.readlines()
data_file.close()
# 用来存放标签和数据
target = []
data = []
print('总计需加载数据个数:' + str(len(data_list)))
# 对每行数据读入
for j in range(len(data_list)):
line_ = data_list[j].split(',') # csv文件每行转列表
numbers = [ int(x)/255 for x in line_[1:] ] # 字符串转数字列表
numbers = np.array(numbers).reshape(28, 28) # 转为np数组,并转换成28*28的形状
target.append(int(line_[0]))
data.append(numbers)
if j % 4000 == 0:
print('已加载 ' + str(j*100/len(data_list))+'%')
target = np.array(target)
data = np.array(data)
print('加载完成!')
return data, target
对于这段代码,想必大家问题应该不大。
04. 卷积层正向传播
在这里为了方便卷积层的使用,我们将专门创建一个用于卷积的类。
# 卷积层模板
class conv:
# 生成卷积模板
def __init__(self):
pass
# 将原图像所感受的局部视野提取出来
def sliding(self):
pass
# 前向传播
def forward(self):
pass
# 反馈修改权重参数
def feedback(self):
pass
这就是卷积层的基本框架。
那么接下来我们来正式的聊一聊卷积:
对于这个我还是很有感觉的,毕竟作为电子信息工程的学生,信号处理类的学科是我们的主要专业方向,而第一次接触卷积的时候是在信号与系统的课程上。而卷积神经网络中的卷积在思想上和信号与系统中的卷积思想相一致。
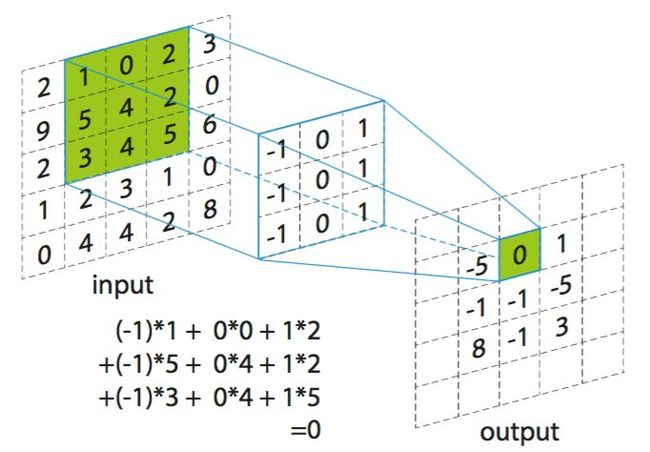
我们来看这张图:
这张图很清楚的呈现了卷积是如何去运算的,但问题也随之而来了,我们原本一个5*5的矩阵,在卷积后却只剩下3*3了,数据量大幅缩水!所以这就是第一个问题,我们该如何保存保证图片边缘不被吞噬呢?
这个问题的解答,如果有同学学习过CV技术,或者是数字图像处理的话,那么解决方法自然就出现了,在图像处理中,我们也会有滤波器对于图像进行滤波处理,可以说和卷积神经网络的这一步简直是双胞胎兄弟,那么为了防止我们滤波一不小心把图像滤没了,我们该怎么办?方法很简单,把原图像扩大一圈即可。至于用什么补足?方法有很多,常见的有补0和将边缘复制一圈。
那么明白这些的话,图像的正向传播可以去写了。如果还不是很清楚,可以参考这位大佬的博客:CNN 入门讲解:什么是卷积(Convolution)
首先我们先把初始化conv的代码完善一下。
# 卷积层模板
class conv:
# 生成卷积模板
def __init__(self, measure, num):
"""
measure: 卷积核的尺寸
num: 卷积核的个数
"""
self.measure = measure
self.num = num
# 随机生成模板,num*measure*measure的卷积核
self.filtres = np.random.randn(num, measure, measure)/(measure**2)
# 为了保持卷积后的图像大小不变,需要在边缘增加一圈数据
self.edge = measure // 2
# 将原图像所感受的局部视野提取出来
def sliding(self, image):
"""
作为一个生成器器,返回图片中的某一局部视野,方便卷积
"""
self.input = image
h, w = image.shape
# 对数据进行填充,使卷积后图形尺寸不变,填充范围为edge,如需了解更多请百度numpy.pad
pad_image = np.pad(image, ((self.edge, self.edge), (self.edge, self.edge)), 'constant', constant_values = (0, 0))
# 迭代生成和卷积模板相卷积的图片中的范围
for i in range(h):
for j in range(w):
iter_image = pad_image[i:(i+self.measure), j:(j+self.measure)]
# 返回局部视野和对应的坐标
yield iter_image, i, j
# 前向传播
def forward(self, input_image):
# 将输入图像保存下来,方便反馈时使用
self.last_input = input_image
h, w = input_image.shape
# 输出的是分别被不同卷积核卷积后的特征图,所以大小为h*w*num
output_image = np.zeros((h, w, self.num))
# 卷积运算
for iter_image, i, j in self.sliding(input_image):
output_image[i, j] = np.sum(iter_image*self.filtres, axis=(1, 2))
# 返回结果
return output_image
# 反馈修改权重参数
def feedback(self):
pass
至此就是卷积层的工作。
这里说一下,卷积核也可以不是一步一步走的,可以跳步,那么具体跳几步就是我们认为定义的了。
05. 池化层正向传播
在之前我们说到池化层,他的主要作用是用作减少数据量,并且保留特征信息。如何减少数据量?说白了不就是把特征图变小嘛~
所以常见的方法有两种,最大池化和平均池化,当然了,方法还有很多,例如:随机池化,中值池化,组合池化等。
那我们这里选择用的是最大池化~
具体的原理参考一下代码就可以理解啦:
# 池化层结构
class pooling:
def __init__(self, poolsize):
# 选择池化的大小
self.size = poolsize
def sliding(self, image):
"""
需要注意的是这里输入的图像是已经经过卷积的三位数组了
"""
self.last_input = image
h = image.shape[0] // self.size
w = image.shape[1] // self.size
# 大致上与卷积的相似,作用是挑选出需要池化的范围
for i in range(h):
for j in range(w):
iter_image = image[(i*self.size):(i*self.size+self.size), (j*self.size):(j*self.size+self.size)]
yield iter_image, i, j
def forward(self, input_image):
# 输出的大小长宽就是原图像/池化大小
output_image = np.zeros((input_image.shape[0] // self.size, input_image.shape[1] // self.size, input_image.shape[2]))
# 对多层特征图循环
for iter_image, i, j in self.sliding(input_image):
# 在每层特征图的范围中选出最大元素
output_image[i, j] = np.amax(iter_image, axis=(0, 1))
return output_image
def feedback(self):
pass
06. softmax层正向传播
为了完成我们的 CNN,我们需要进行具体的预测。通过 softmax 来实现,将一组数字转换为一组概率,总和为 1。在手写数字识别中,我们需要输出的可能值分别有0到9 是个数字,所以我们的输出节点共有10个,分别代表各自的概率。
在这里我们用交叉熵来计算概率之间的距离【信息论的知识,实话实说,在学习的过程中真感觉电子信息学人工智能好对口啊】:
I ( p , q ) = − ∑ x p ( x ) ln ( q ( x ) ) I(p,q)=- \sum _{x}p(x) \ln (q(x)) I(p,q)=−x∑p(x)ln(q(x))
其中 p ( x ) p(x) p(x) 为正式的概率, q ( x ) q(x) q(x)为预测概率。又因为真实概率的结果固定为1或者0,所以其最终的值为 − ln ( p c ) -\ln(p_c) −ln(pc), 换句话说就是 e p ( c ) e^{p(c)} ep(c),即正确分类的预测概率。由代码体现如下
class softmax:
def __init__(self, input_size, outnodes):
# 权重文件,该层的输入节点全连接输出节点
self.weights = np.random.randn(input_size, outnodes) / input_size
# 输出节点偏置
self.output = np.zeros(outnodes)
def forward(self, input_image):
self.last_input_shape = input_image.shape
input_image = input_image.flatten() # 将数据转化成一维
self.last_input = input_image # 将该层节点记录下来,用作反馈
length, nodes = self.weights.shape
# 最后的概率, totals是尺寸为outnodes的一维数组
totals = np.dot(input_image, self.weights) + self.output
self.last_totals = totals
# 结论
out = np.exp(totals)
# 将归一化后的结果返回
return out / np.sum(out, axis=0)
def feedback(self):
pass
有需要关注softmax具体推导等的同学可以关注这篇博客一文详解Softmax函数 - 知乎 (zhihu.com)
至此,我们的前向传播函数正式ending!
07. CNN模型
接下来,我们需要把整个CNN模型给搭建出来了,在这个模型中,我们需要有训练用的方法,也需要有预测的方法。在之前全连接的神经网络中,我们知道,训练的函数是在测试的函数后加入了反馈的过程,于是我们便得到了他:
class CNN:
def __init__(self, convsize, poolsize, image_size, channel, classis):
"""
convsize : 卷积核视野的大小
poolsize : 池化范围大小
imagesize: 图片的尺寸
channel : 卷积核的层数
classis : 分类数
"""
# 定义一个卷积层
self.conv3 = conv(convsize, channel)
# 定义一个池化层
self.pool2 = pooling(poolsize)
# 定义一个softmax层
self.softmax_ = softmax((image_size[0]//poolsize)*(image_size[1]//poolsize)*channel, classis)
# 训练过程
def train(self, images, target, wheel, learn_rate):
"""
images : 训练用的图片组
target : 训练用的答案
wheel : 训练的轮数
learn_rate: 学习率
"""
# 记录损失的函数
loss = []
for i in range(wheel):
item_loss = 0 # 每轮损失函数计算
for image in range(len(images)):
# 数据的正向传播
out = self.conv3.forward(images[image])
out = self.pool2.forward(out)
out = self.softmax_.forward(out)
# 损失值计算
item_loss += -np.log(out[target[image]])
# 反馈数据
# 仅关注正确标签,初始反馈的函数为 (-1/正确答案对应的概率)
gradient = np.zeros(10)
gradient[target[image]] = -1 / out[target[image]]
gradient = self.softmax_.feedback(gradient, learn_rate)
gradient = self.pool2.feedback(gradient)
gradient = self.conv3.feedback(gradient, learn_rate)
loss.append(item_loss / len(wheel))
return loss
# 测试函数
def test(self, image):
# 测试函数仅包含正向传播
out = self.conv3.forward(image)
out = self.pool2.forward(out)
out = self.softmax_.forward(out)
return out, np.argmax(out)
接下来就是构建我们的反馈函数了。
08. softmax层反馈
我们现在可以知道softmax层是用来输出结果的一层,而现在我们需要从这里将数据反馈回去。从CNN的框架中,我们可以看到,我们的反馈是一层一层逐步回退的,现在我们开始具体实现吧~
class softmax:
def __init__(self, input_size, outnodes):
# 权重文件,该层的输入节点全连接输出节点
self.weights = np.random.randn(input_size, outnodes) / input_size
# 输出节点偏置
self.output = np.zeros(outnodes)
def forward(self, input_image):
self.last_input_shape = input_image.shape
input_image = input_image.flatten() # 将数据转化成一维
self.last_input = input_image # 将该层节点记录下来,用作反馈
length, nodes = self.weights.shape
# 最后的概率, totals是尺寸为outnodes的一维数组
totals = np.dot(input_image, self.weights) + self.output
self.last_totals = totals
# 结论
out = np.exp(totals)
# 将归一化后的结果返回
return out / np.sum(out, axis=0)
def feedback(self, gradients, learn_rate):
"""
gradients : 反馈回来的梯度组,目前仅是正确答案所对应的下标有正确值
learn_rate: 学习率
"""
# 找到正确答案所对应的那个gradient
for i, gradient in enumerate(gradients):
if gradient == 0:
continue
# 得到一群1和一个正确答案所对应的非1值
exps = np.exp(self.last_totals)
s = np.sum(exps)
# 反馈的数值,具体公式见注1
out_back = -exps[i] * exps / (s ** 2)
out_back[i] = exps[i] * (s - exps[i]) / (s ** 2)
# 将反馈数值和概率做乘积,得到结果权重1
out_back = gradient * out_back
# @ 可以理解成矩阵乘法
# 最后的输出与结果反馈的权重做点乘,获得权重的偏置
weight_back = self.last_input[np.newaxis].T @ out_back[np.newaxis]
inputs_back = self.weights @ out_back
self.weights -= learn_rate * weight_back
self.output -= learn_rate * out_back
# 将矩阵从 1d 转为 3d
# 1352 to 13x13x8
return inputs_back.reshape(self.last_input_shape)
注1:
∂ o u t a ( k ) ∂ t = { − e t c e t k S 2 i f k ≠ c e t c ( S − e t c S 2 i f k = c \frac{ \partial out_{a}(k)}{ \partial t}= \begin{cases} \frac{-e^{t_{c}}e^{t_{k}}}{S^{2}} if k \neq c \\\\ \frac{e^{t_{c}}(S-e^{t_{c}}}{S^{2}}ifk=c \end{cases} ∂t∂outa(k)=⎩⎪⎨⎪⎧S2−etcetkifk=cS2etc(S−etcifk=c
具体的公式推导这里无了,太累了。
09. 池化层反馈
池化层的反馈与其说是反馈,到不如说是走个形式,为什么这么说呢?看代码~
# 池化层结构
class pooling:
def __init__(self, poolsize):
# 选择池化的大小
self.size = poolsize
def sliding(self, image):
"""
需要注意的是这里输入的图像是已经经过卷积的三位数组了
"""
self.last_input = image
h = image.shape[0] // self.size
w = image.shape[1] // self.size
# 大致上与卷积的相似,作用是挑选出需要池化的范围
for i in range(h):
for j in range(w):
iter_image = image[(i*self.size):(i*self.size+self.size), (j*self.size):(j*self.size+self.size)]
yield iter_image, i, j
def forward(self, input_image):
# 输出的大小长宽就是原图像/池化大小
output_image = np.zeros((input_image.shape[0] // self.size, input_image.shape[1] // self.size, input_image.shape[2]))
# 对多层特征图循环
for iter_image, i, j in self.sliding(input_image):
# 在每层特征图的范围中选出最大元素
output_image[i, j] = np.amax(iter_image, axis=(0, 1))
return output_image
def feedback(self, backnodes):
# 池化层输入数据,26x26x8,默认初始化为 0
inputnodes = np.zeros(self.last_input.shape)
# 每一个 iter_image 都是一个 3x3x8 的8层小矩阵
# 修改 max 的部分,首先查找 max
for iter_image, i, j in self.sliding(self.last_input):
h, w, f = iter_image.shape
# 获取 iter_image 里面最大值的索引向量,一叠的感觉
amax = np.amax(iter_image, axis=(0, 1))
# 遍历整个 iter_image,对于传递下去的像素点,修改 gradient 为 loss 对 output 的gradient
for i2 in range(h):
for j2 in range(w):
for f2 in range(f):
# 如果这个像素是最大值,复制梯度到它。
if iter_image[i2, j2, f2] == amax[f2]:
inputnodes[i * self.size + i2, j * self.size + j2, f2] = backnodes[i, j, f2]
return inputnodes
是不是很简单,笑哭。
10.卷积层反馈
卷积层说是我们CNN的核心,但是在反馈上相对于前面来说也并不复杂,
# 卷积层模板
class conv:
# 生成卷积模板
def __init__(self, measure, num):
"""
measure: 卷积核的尺寸
num: 卷积核的个数
"""
self.measure = measure
self.num = num
# 随机生成模板,num*measure*measure的卷积核
self.filtres = np.random.randn(num, measure, measure)/(measure**2)
# 为了保持卷积后的图像大小不变,需要在边缘增加一圈数据
self.edge = measure // 2
# 将原图像所感受的局部视野提取出来
def sliding(self, image):
"""
作为一个生成器器,返回图片中的某一局部视野,方便卷积
"""
self.input = image
h, w = image.shape
# 对数据进行填充,使卷积后图形尺寸不变,填充范围为edge,如需了解更多请百度numpy.pad
pad_image = np.pad(image, ((self.edge, self.edge), (self.edge, self.edge)), 'constant', constant_values = (0, 0))
# 迭代生成和卷积模板相卷积的图片中的范围
for i in range(h):
for j in range(w):
iter_image = pad_image[i:(i+self.measure), j:(j+self.measure)]
# 返回局部视野和对应的坐标
yield iter_image, i, j
# 前向传播
def forward(self, input_image):
# 将输入图像保存下来,方便反馈时使用
self.last_input = input_image
h, w = input_image.shape
# 输出的是分别被不同卷积核卷积后的特征图,所以大小为h*w*num
output_image = np.zeros((h, w, self.num))
# 卷积运算
for iter_image, i, j in self.sliding(input_image):
output_image[i, j] = np.sum(iter_image*self.filtres, axis=(1, 2))
# 返回结果
return output_image
# 反馈修改权重参数
def feedback(self, out, learn_rate):
# 申请一个和卷积核相仿的数组
filters = np.zeros(self.filtres.shape)
for iter_image, i, j in self.sliding(self.last_input):
for f in range(self.num):
# 将反馈回来的卷积层权重和模板走上一遭,并对模板进行修正,因为之间的的反馈数据都包含着图像感兴趣的点
filters[f] += out[i,j,f] * iter_image
self.filtres -= learn_rate * filters
至此,我们的目标就实现了,那么还有一些渲染的过程可以加入~
11. 动态绘图
如何使将训练时候的损失函数更好的展示出来呢? 这里我想到的是用动态绘图的方式,具体代码修改CNN中的图如下如下
class CNN:
def __init__(self, convsize, poolsize, image_size, channel, classis):
"""
convsize : 卷积核视野的大小
poolsize : 池化范围大小
imagesize: 图片的尺寸
channel : 卷积核的层数
classis : 分类数
"""
# 定义一个卷积层
self.conv3 = conv(convsize, channel)
# 定义一个池化层
self.pool2 = pooling(poolsize)
# 定义一个softmax层
self.softmax_ = softmax((image_size[0]//poolsize)*(image_size[1]//poolsize)*channel, classis)
# 训练过程
def train(self, images, target, wheel, learn_rate):
"""
images : 训练用的图片组
target : 训练用的答案
wheel : 训练的轮数
learn_rate: 学习率
"""
# 记录损失的函数
loss = []
# 计次
item = 0
# 绘图窗口打开
plt.ion()
for i in range(wheel):
item_loss = 0 # 每轮损失函数计算
for image in range(len(images)):
# 数据的正向传播
out = self.conv3.forward(images[image])
out = self.pool2.forward(out)
out = self.softmax_.forward(out)
# 损失值计算
item_loss += -np.log(out[target[image]])
# 反馈数据
# 仅关注正确标签,初始反馈的函数为 (-1/正确答案对应的概率)
gradient = np.zeros(10)
gradient[target[image]] = -1 / out[target[image]]
gradient = self.softmax_.feedback(gradient, learn_rate)
gradient = self.pool2.feedback(gradient)
gradient = self.conv3.feedback(gradient, learn_rate)
item += 1
if item % 200 == 0:
plt.clf() # 清除之前画的图
loss.append(item_loss/200)
plt.plot(loss)
plt.pause(0.001)
print("process: %.4f loss: %.7f" % (item / (wheel * len(images)), item_loss/200))
item_loss = 0
plt.ioff()
return loss
# 测试函数
def test(self, image):
# 测试函数仅包含正向传播
out = self.conv3.forward(image)
out = self.pool2.forward(out)
out = self.softmax_.forward(out)
return out, np.argmax(out)
12. 全部代码
import numpy as np
import matplotlib.pyplot as plt
# 读入文件的地址,返回数据集的数据和标签
def read_data(path):
print("数据加载ing...")
data_file = open(path, 'r')
data_list = data_file.readlines()
data_file.close()
# 用来存放标签和数据
target = []
data = []
print('总计需加载数据个数:' + str(len(data_list)))
# 对每行数据读入
for j in range(len(data_list)):
line_ = data_list[j].split(',') # csv文件每行转列表
numbers = [ int(x)/255 for x in line_[1:] ] # 字符串转数字列表
numbers = np.array(numbers).reshape(28, 28) # 转为np数组,并转换成28*28的形状
target.append(int(line_[0]))
data.append(numbers)
if j % 4000 == 0:
print('已加载 ' + str(j*100/len(data_list))+'%')
target = np.array(target)
data = np.array(data)
print('加载完成!')
return data, target
# 卷积层模板
class conv:
# 生成卷积模板
def __init__(self, measure, num):
"""
measure: 卷积核的尺寸
num: 卷积核的个数
"""
self.measure = measure
self.num = num
# 随机生成模板,num*measure*measure的卷积核
self.filtres = np.random.randn(num, measure, measure)/(measure**2)
# 为了保持卷积后的图像大小不变,需要在边缘增加一圈数据
self.edge = measure // 2
# 将原图像所感受的局部视野提取出来
def sliding(self, image):
"""
作为一个生成器器,返回图片中的某一局部视野,方便卷积
"""
self.input = image
h, w = image.shape
# 对数据进行填充,使卷积后图形尺寸不变,填充范围为edge,如需了解更多请百度numpy.pad
pad_image = np.pad(image, ((self.edge, self.edge), (self.edge, self.edge)), 'constant', constant_values = (0, 0))
# 迭代生成和卷积模板相卷积的图片中的范围
for i in range(h):
for j in range(w):
iter_image = pad_image[i:(i+self.measure), j:(j+self.measure)]
# 返回局部视野和对应的坐标
yield iter_image, i, j
# 前向传播
def forward(self, input_image):
# 将输入图像保存下来,方便反馈时使用
self.last_input = input_image
h, w = input_image.shape
# 输出的是分别被不同卷积核卷积后的特征图,所以大小为h*w*num
output_image = np.zeros((h, w, self.num))
# 卷积运算
for iter_image, i, j in self.sliding(input_image):
output_image[i, j] = np.sum(iter_image*self.filtres, axis=(1, 2))
# 返回结果
return output_image
# 反馈修改权重参数
def feedback(self, out, learn_rate):
# 申请一个和卷积核相仿的数组
filters = np.zeros(self.filtres.shape)
for iter_image, i, j in self.sliding(self.last_input):
for f in range(self.num):
# 将反馈回来的卷积层权重和模板走上一遭,并对模板进行修正,因为之间的的反馈数据都包含着图像感兴趣的点
filters[f] += out[i,j,f] * iter_image
self.filtres -= learn_rate * filters
# 池化层结构
class pooling:
def __init__(self, poolsize):
# 选择池化的大小
self.size = poolsize
def sliding(self, image):
"""
需要注意的是这里输入的图像是已经经过卷积的三位数组了
"""
self.last_input = image
h = image.shape[0] // self.size
w = image.shape[1] // self.size
# 大致上与卷积的相似,作用是挑选出需要池化的范围
for i in range(h):
for j in range(w):
iter_image = image[(i*self.size):(i*self.size+self.size), (j*self.size):(j*self.size+self.size)]
yield iter_image, i, j
def forward(self, input_image):
# 输出的大小长宽就是原图像/池化大小
output_image = np.zeros((input_image.shape[0] // self.size, input_image.shape[1] // self.size, input_image.shape[2]))
# 对多层特征图循环
for iter_image, i, j in self.sliding(input_image):
# 在每层特征图的范围中选出最大元素
output_image[i, j] = np.amax(iter_image, axis=(0, 1))
return output_image
def feedback(self, backnodes):
# 池化层输入数据,26x26x8,默认初始化为 0
inputnodes = np.zeros(self.last_input.shape)
# 每一个 iter_image 都是一个 3x3x8 的8层小矩阵
# 修改 max 的部分,首先查找 max
for iter_image, i, j in self.sliding(self.last_input):
h, w, f = iter_image.shape
# 获取 iter_image 里面最大值的索引向量,一叠的感觉
amax = np.amax(iter_image, axis=(0, 1))
# 遍历整个 iter_image,对于传递下去的像素点,修改 gradient 为 loss 对 output 的gradient
for i2 in range(h):
for j2 in range(w):
for f2 in range(f):
# 如果这个像素是最大值,复制梯度到它。
if iter_image[i2, j2, f2] == amax[f2]:
inputnodes[i * self.size + i2, j * self.size + j2, f2] = backnodes[i, j, f2]
return inputnodes
class softmax:
def __init__(self, input_size, outnodes):
# 权重文件,该层的输入节点全连接输出节点
self.weights = np.random.randn(input_size, outnodes) / input_size
# 输出节点偏置
self.output = np.zeros(outnodes)
def forward(self, input_image):
self.last_input_shape = input_image.shape
input_image = input_image.flatten() # 将数据转化成一维
self.last_input = input_image # 将该层节点记录下来,用作反馈
length, nodes = self.weights.shape
# 最后的概率, totals是尺寸为outnodes的一维数组
totals = np.dot(input_image, self.weights) + self.output
self.last_totals = totals
# 结论
out = np.exp(totals)
# 将归一化后的结果返回
return out / np.sum(out, axis=0)
def feedback(self, gradients, learn_rate):
"""
gradients : 反馈回来的梯度组,目前仅是正确答案所对应的下标有正确值
learn_rate: 学习率
"""
# 找到正确答案所对应的那个gradient
for i, gradient in enumerate(gradients):
if gradient == 0:
continue
# 得到一群1和一个正确答案所对应的非1值
exps = np.exp(self.last_totals)
s = np.sum(exps)
# 反馈的数值,具体公式见注1
out_back = -exps[i] * exps / (s ** 2)
out_back[i] = exps[i] * (s - exps[i]) / (s ** 2)
# 将反馈数值和概率做乘积,得到结果权重1
out_back = gradient * out_back
# @ 可以理解成矩阵乘法
# 最后的输出与结果反馈的权重做点乘,获得权重的偏置
weight_back = self.last_input[np.newaxis].T @ out_back[np.newaxis]
inputs_back = self.weights @ out_back
self.weights -= learn_rate * weight_back
self.output -= learn_rate * out_back
# 将矩阵从 1d 转为 3d
# 1352 to 13x13x8
return inputs_back.reshape(self.last_input_shape)
class CNN:
def __init__(self, convsize, poolsize, image_size, channel, classis):
"""
convsize : 卷积核视野的大小
poolsize : 池化范围大小
imagesize: 图片的尺寸
channel : 卷积核的层数
classis : 分类数
"""
# 定义一个卷积层
self.conv3 = conv(convsize, channel)
# 定义一个池化层
self.pool2 = pooling(poolsize)
# 定义一个softmax层
self.softmax_ = softmax((image_size[0]//poolsize)*(image_size[1]//poolsize)*channel, classis)
# 训练过程
def train(self, images, target, wheel, learn_rate):
"""
images : 训练用的图片组
target : 训练用的答案
wheel : 训练的轮数
learn_rate: 学习率
"""
# 记录损失的函数
loss = []
# 计次
item = 0
# 绘图窗口打开
plt.ion()
for i in range(wheel):
item_loss = 0 # 每轮损失函数计算
for image in range(len(images)):
# 数据的正向传播
out = self.conv3.forward(images[image])
out = self.pool2.forward(out)
out = self.softmax_.forward(out)
# 损失值计算
item_loss += -np.log(out[target[image]])
# 反馈数据
# 仅关注正确标签,初始反馈的函数为 (-1/正确答案对应的概率)
gradient = np.zeros(10)
gradient[target[image]] = -1 / out[target[image]]
gradient = self.softmax_.feedback(gradient, learn_rate)
gradient = self.pool2.feedback(gradient)
gradient = self.conv3.feedback(gradient, learn_rate)
item += 1
if item % 200 == 0:
plt.clf() # 清除之前画的图
loss.append(item_loss/200)
plt.plot(loss)
plt.pause(0.001)
print("process: %.4f loss: %.7f" % (item / (wheel * len(images)), item_loss/200))
item_loss = 0
plt.ioff()
return loss
# 测试函数
def test(self, image):
# 测试函数仅包含正向传播
out = self.conv3.forward(image)
out = self.pool2.forward(out)
out = self.softmax_.forward(out)
return out, np.argmax(out)
叁、跑一跑模型
实话实说,这么幸苦的写了一个模型不玩玩肯定是不可能的,所以让我们来运行运行玩玩~
写一下运行的脚本:
demo = CNN(3, 2, [28, 28], 3, 10)
data, target = read_data('mnist_train.csv')
demo.train(data, target, 1, 0.001)
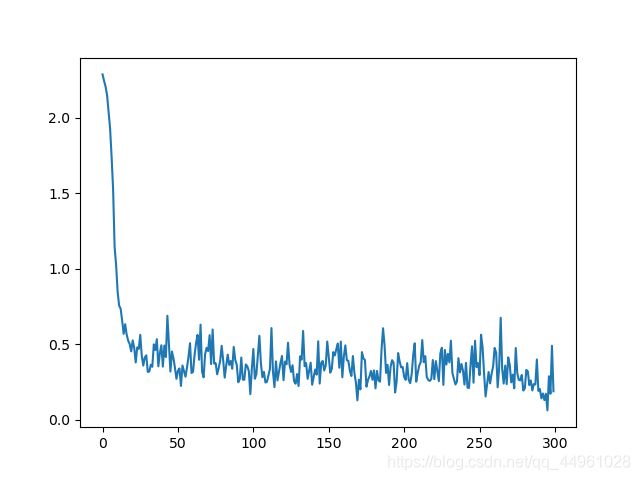
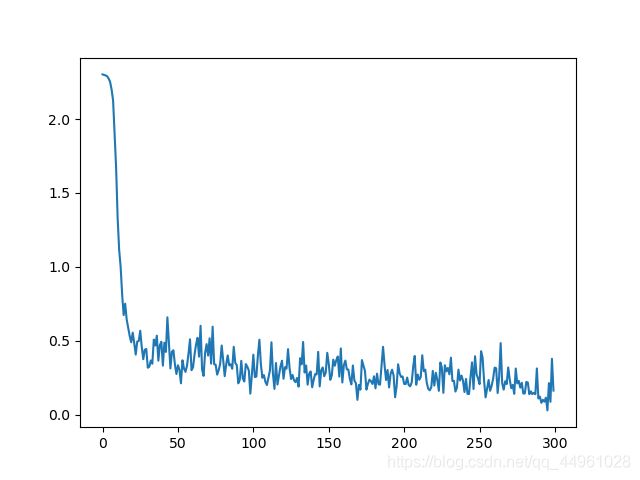
大致上看了一下,效果还不错,首先看一下loss图:
随后我们可以在测试集上进行测试:
data2, target2 = read_data('mnist_test.csv')
count = 0
item_loss = 0
for item in range(len(data2)):
out, result = demo.test(data2[item])
if result == target2[item]:
count += 1
item_loss += -np.log(out[target2[item]])
print("准确率为:", count/(len(data2)))
print("average_loss:", item_loss/(len(data2)))
准确率为: 0.8977
average_loss: 0.3368406190461122
在用时上不到一个小时,对比NN我们可以发现,在相近的准确率上CNN会更加快速。
但这就是极限吗?准确度就止步于此了吗?我们现在所用的CNN有很多可调参数,接下来我们来一一探寻!
肆、调参以及思考
回顾一下我们运行的脚本,我们可以看到无论是卷积核还是卷积核的个数,又或者是池化大小学习率等都是可调整的,那么接下来我们就来尝试一下吧。
关于池化
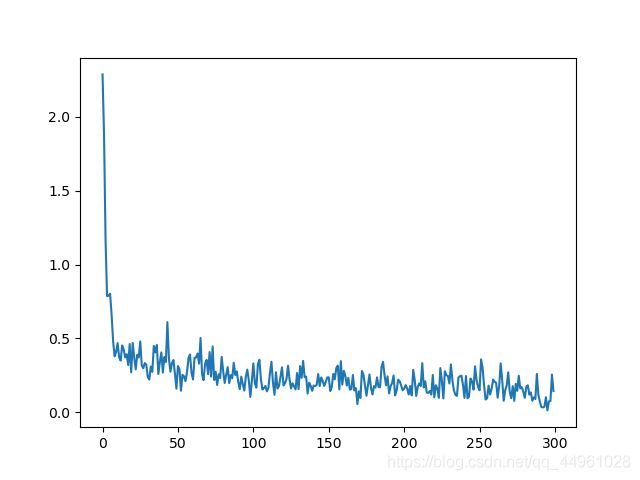
首先我们可以增加池化大小,在之前的训练中,我们池化大小是2,现在我们调整到4来看看:
demo = CNN(3, 4, [28, 28], 3, 10)
data, target = read_data('mnist_train.csv')
demo.train(data, target, 1, 0.001)
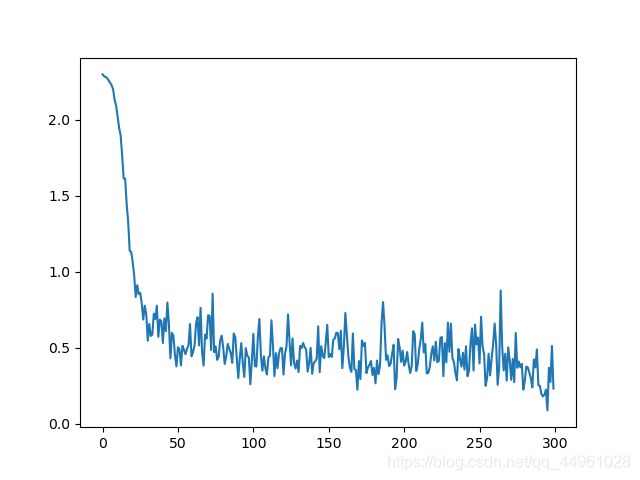
从结果中我们可以看到,总计耗时,我们和之前对比一下发现:
池化为4的时候
准确率为: 0.8656
average_loss: 0.43426243230812334
用时27min50s
池化为2的时候
准确率为: 0.8656
average_loss: 0.43426243230812334
用时30min25s
所以我们可以得出结论1:
池化范围增大,准确率下降,用时缩短【原理还是简单的,池化范围越大,对于原图数据的感知越模糊】
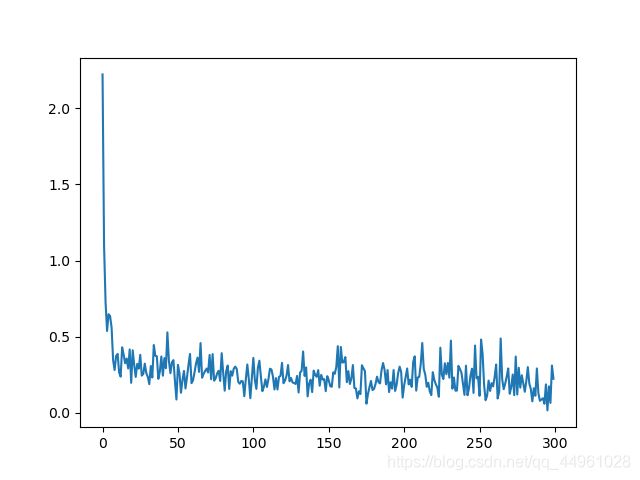
关于卷积核大小
demo = CNN(7, 2, [28, 28], 3, 10)
data, target = read_data('mnist_train.csv')
demo.train(data, target, 1, 0.001)
结果对比原数据来看。
卷积核大小为7的时候
准确率为: 0.9314
average_loss: 0.22480404055570863
从结果对比上,我们可以发现卷积核放大后,准确率有明显上升,但用是更长了.
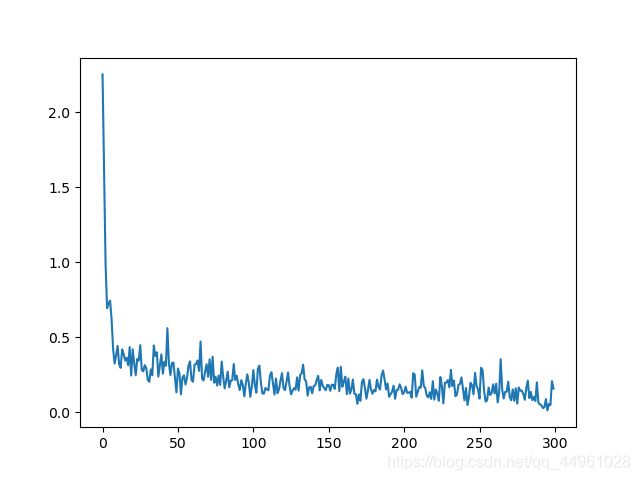
关于学习率
demo = CNN(7, 2, [28, 28], 3, 10)
data, target = read_data('mnist_train.csv')
demo.train(data, target, 1, 0.005)
学习率为0.005的时候
准确率为: 0.9531
average_loss: 0.15126643409196025
我们继续增大学习率
demo = CNN(7, 2, [28, 28], 3, 10)
data, target = read_data('mnist_train.csv')
demo.train(data, target, 1, 0.01)
学习率为0.01的时候
准确率为: 0.9417
average_loss: 0.19984729973377996
对比后我们可以发现,学习率并非越高越好,学习率有一个稳定适合的值是最好的。【证明公式可以参考一下梯度下降】
关于卷积核的个数
demo = CNN(7, 2, [28, 28], 8, 10)
data, target = read_data('mnist_train.csv')
demo.train(data, target, 1, 0.005)
卷积核个数为8的时候
准确率为: 0.9613
average_loss: 0.12449047922167399
从这个角度来看,卷积核个数可以提高准确率,但同时也会提高时间的损耗。
迭代次数
这部分就没有图了,但我确实运行了。
demo = CNN(7, 2, [28, 28], 8, 10)
data, target = read_data('mnist_train.csv')
demo.train(data, target, 3, 0.005)
迭代三轮的时候
准确率为: 0.9694
average_loss: 0.09630516698175499
可以看到这里迭代次数对于准确率是由提高的,但随着时间的增长,效果越弱。
总结
从这次试验来看,CNN的表现效果明显强过全连接神经网络,并且最优可以达到将近97%的准确率,其中比较欠缺的是还没有加入全连接层和没有加入激活函数,但对于本次的实验来看,效果还是令人满意的。
好的,到了这里我也算是比较满意的对CNN的学习告一段落了【其实还有一些感兴趣的,不过就不在这里一一写完了,时间不允许了】。希望这篇博客可以对大家有所帮助。