EM算法与GMM算法

• EM是GMM的基础，即高斯混合模型

• 基础知识点：方差、协方差、高斯分布、极大似然估计、贝叶斯公式、K-means算法

• jensen不等式：$f(\theta x+(1-\theta )y)\le \theta f(x)+(1-\theta )f(y)$
  $$f(\mathbf{E}x)\le \mathbf{E}f(x)$$

EM算法

算法引入

• E-step：概率计算
• M-step：贝叶斯公式计算概率

算法原理

• 给定的m个训练样本$\{x(1),x(2),\dots .,x(m)\}$，样本间独立$\theta$，找出样本的模型参数，极大化模型分布的对数似然函数如些：
  $$\theta =\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^m\log \left(P\left(x^{(i)};\theta \right)\right)$$

• 假定样本数据中存在隐含数据$z=\{z(1),z(2),\dots ,z(k)\}$，此时极大化模型分布的对数似然函数如下：
  $$\begin{array}{rl}l(\theta )& =\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^m\log \left(P\left(x^{(i)};\theta \right)\right)\\ & =\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^m\log \left(\sum _{z=1}^{m}P\left(x^{(i)},z^{(i)};\theta \right)\right)\end{array}$$

• Z是隐随机变量，不方便直接找到参数估计。策略：计算$l(\theta )$的下界，求该下界最大值，重复该过程，直到收敛到局部最大值

• 令z的分布为$Q(z;\theta )$，并且$\mathrm{Q}(z;\theta )\ge 0$；那么有如下公式：
  $$\begin{array}{l}\begin{array}{rl}l(\theta )& =\sum _{l=1}^m\log \sum _{z}p(x,z;\theta )\\ & =\sum _{i=1}^m\log \sum _{z}Q(z;\theta )\cdot \frac{p(x,z;\theta )}{Q(z;\theta )}\\ & =\sum _{i=1}^m\log \left(E_Q\left(\frac{p(x,z;\theta )}{Q(z;\theta )}\right)\right)\\ & \ge \sum _{i=1}^m{E}_l\left(\log \left(\frac{p(x,z;\theta )}{Q(z;\theta )}\right)\right)\\ & =\sum _{i=1}^m\sum _{z}Q(z;\theta )\log \left(\frac{p(x,z;\theta )}{Q(z;\theta )}\right)\end{array}\end{array}$$

• 当且仅当x1=x2，取等号

• 根据jensen不等式的特性，当$\frac{p(x,z;\theta )}{Q(z;\theta )}=c$时，$l(\theta )$函数才能取等号

  $l(\theta )\ge {\sum }_{i=1}^m{E}_Q\left(\log \left(\frac{p(x,z;\theta )}{Q(z;\theta )}\right)\right)$、${\sum }_{z}Q(z;\theta )=1$

  $Q(z,\theta )=\frac{p(x,z;\theta )}{c}=\frac{p(x,z;\theta )}{c\cdot {\sum }_{z^{\prime }}Q\left(z^i;\theta \right)}$=$\frac{p(x,z;\theta )}{{\sum }_{z^{\prime }}c\left(z^{\prime };\theta \right)}=\frac{p(x,z;\theta )}{{\sum }_{z^{\prime }}p\left(x,z^{\prime };\theta \right)}=\frac{p(x,z;\theta )}{p(x;\theta )}=p(z|x;\theta )$

• $l(\theta )=\underset{\theta }{\mathrm{argmax}}l(\theta )=\underset{\theta }{\mathrm{argmax}}{\sum }_{i=1}^m{\sum }_{z}Q(z;\theta )\log \left(\frac{p(x,z;\theta )}{Q(z;\theta )}\right)$

  $=\underset{\theta }{\mathrm{argmax}}{\sum }_{i=1}^m{\sum }_{z}Q(z|x;\theta )\log \left(\frac{p(x,z;\theta )}{Q(z|x;\theta )}\right)$

  $=\underset{\theta }{\mathrm{argmax}}{\sum }_{i=1}^m{\sum }_{z}Q(z|x;\theta )\log (p(x,z;\theta ))$

算法流程

样本数据，联合分布，条件分布，最大迭代次数J

• 随机初始化模型参数$\theta$的初始值${\theta }^0$
• 开始EM算法的迭代处理：

  • E步：计算联合分布的条件概率期望：

    $l(\theta )={\sum }_{i=1}^m{\sum }_{z}Q(z|x;{\theta }^j)\log (p(x,z;{\theta }^j))$

  • M步：极大化L函数，得到${\theta }^{j+1}$，${\theta }^{j+1}=\arg \max l(\theta )$

  • 如果${\theta }_{j+1}$收敛，则算法结束，输出参数，否则继续迭代处理

GMM

算法概述

• GMM(Gaussian Mixture Model, 高斯混合模型)是指该算法油多个高斯模型线性叠加混合而成。 每个高斯模型称之为component。GMM算法描述的是数据的本身存在的一种分布。

• GMM算法常用于聚类应用中，component的个数就可以认为是类别的数量。

• 假定GMM由k个Gaussian分布线性叠加而成，那么概率密度函数如下：

  $p(x)={\sum }_{k=1}^{k}p(k)p(x|k)={\sum }_{k=1}^k{\pi }_{k}p(x;{\mu }_k,{\Sigma }_k)$

  

• 对数似然函数为：$l(\pi ,\mu ,\sigma )={\sum }_{i=1}^{N}log({\sum }_{k=1}^k{\pi }_{k}p(x^i;{\mu }_k,{\Sigma }_k))$

算法求解

• E步：$w_j^{(i)}=Q_i\left(z^{(i)}=j\right)=p\left(z^{(i)}=j|x^{(i)};\pi ,\mu ,\Sigma \right)$

• M步：

  $$\begin{array}{rl}l(\pi ,\mu ,\Sigma )& =\sum _{i=1}^m\sum _{z^n}{Q}_i\left(z^{(i)}\right)\log \left(\frac{p\left(x^{(i)},z^{(i)};\pi ,\mu ,\Sigma \right)}{Q_i\left(z^{(i)}\right)}\right)\\ & =\sum _{i=1}^m\sum _{j=1}^k{Q}_i\left(z^{(i)}=j\right)\log \frac{p\left(x^{(i)}|z^{(i)}=j;\mu ,\Sigma \right)\cdot p\left(z^{(i)}=j;\pi \right)}{Q_i\left(z^{(i)}=j\right)}\\ & =\sum _{i=1}^m\sum _{j=1}^k{w}_j^{(i)}\log \frac{\left(\frac{1}{(2\pi {)}^{\frac{n}{2}}{|{\Sigma }_j|}^{\frac{1}{2}}}{e}^{\frac{-\frac{1}{2}(x^{(i)}-{\mu }_j{)}^T\cdot (x^{(i)}-{\mu }_j)}{{\Sigma }_j}}\right)\cdot {\pi }_j}{w_j^{(i)}})\end{array}$$

• 对均值求偏导：

  $\begin{array}{rl}l(\pi ,\mu ,\Sigma )& =\sum _{i=1}^m\sum _{j=1}^k{w}_j^{(i)}\left(-\frac{1}{2}{\left(x^{(i)}-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(x^{(i)}-{\mu }_j\right)\right)+c\\ \frac{\partial l}{\partial {\mu }_l}=& -\frac{1}{2}\sum _{i=1}^m{w}_l^{(i)}\left(x^{(i{)}^T}{\Sigma }_l^{-1}{x}^{(i)}-x^{(i{)}^T}{\Sigma }_l^{-1}{\mu }_l-{\mu }_l^T{\Sigma }_l^{-1}{x}^{(i)}+{\mu }_l^T{\Sigma }_l^{-1}{\mu }_l\right)\\ & =\frac{1}{2}\sum _{i=1}^m{w}_l^{(i)}\left({\left(x^{(i{)}^T}{\Sigma }_l^{-1}\right)}^T+{\Sigma }_l^{-1}{x}^{(i)}-\left({\left({\Sigma }_l^{-1}\right)}^T+{\Sigma }_l^{-1}\right){\mu }_l\right)\\ & =\sum _{i=1}^m{w}_l^{(i)}\left({\Sigma }_l^{-1}{x}^{(i)}-{\Sigma }_l^{-1}{\mu }_l\right)\end{array}$

  $\frac{\partial l}{\partial {\mu }_l}=0$→${\mu }_l=\frac{{\sum }_{i=1}^m{w}_l^{(i)}{x}^{(i)}}{{\sum }_{i=1}^m{w}_l^{(i)}}$

• 对方差求偏导：

  $\begin{array}{rl}l(\pi ,\mu ,\Sigma )=& \frac{1}{2}\sum _{i=1}^m\sum _{j=1}^k{w}_j^{(i)}\left(\log {\Sigma }_j^{-1}-{\left(x^{(i)}-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(x^{(i)}-{\mu }_j\right)\right)+c\\ \frac{\partial l}{\partial {\Sigma }_l}=& \frac{1}{2}\sum _{i=1}^m{w}_i^{(i)}\left({\Sigma }_l-\left(x^{(i)}-{\mu }_j\right){\left(x^{(i)}-{\mu }_j\right)}^T\right)\\ \stackrel{\hat{y}\frac{\partial l}{\partial L_l}=0}{\partial z_l}& {\Sigma }_l=\frac{{\sum }_{i=1}^m{w}_l^{(i)}\left(x^{(i)}-{\mu }_l\right){\left(x^{(i)}-{\mu }_l\right)}^T}{{\sum }_{i=1}^m{w}_l^{(i)}}\end{array}$

• 对概率使用拉格朗日乘子法求解：

  $l(\pi ,\mu ,\Sigma )={\sum }_{i=1}^m{\sum }_{j=1}^k{w}_j^{(j)}\log {\pi }_j+c$ s.t $:{\sum }_{j=1}^k{\pi }_j=1$

  $\begin{array}{r}L(\pi )=\sum _{i=1}^m\sum _{j=1}^k{w}_j^{(i)}\log {\pi }_j+\beta \left(\sum _{j=1}^k{\pi }_j-1\right)\\ \frac{\partial L}{\partial {\pi }_l}=\sum _{i=1}^m\frac{w_l^{(i)}}{{\pi }_l}+\beta \frac{\hat{\gamma }\frac{\partial L}{\partial {\pi }_l=0}}{⟶}{\pi }_l=\frac{1}{m}\sum _{i=1}^m{w}_l^{(i)}\end{array}$

代码实战

底层实现

# -*- coding: utf-8 -*-
#@Author    : huinono
#@Software  : PyCharm

import copy
import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = 'False'

class GMM_study():
    def __init__(self):
        pass

    def generate_data(self,sigma, N, mu1, mu2, mu3, mu4, alpha):
        global X  # 可观测数据集
        X = np.zeros((N, 2))  # 初始化X，2行N列。2维数据，N个样本
        X = np.matrix(X)
        global mu  # 随机初始化mu1，mu2，mu3，mu4
        mu = np.random.random((4, 2))
        mu = np.matrix(mu)
        global excep  # 期望第i个样本属于第j个模型的概率的期望
        excep = np.zeros((N, 4))
        global alpha_  # 初始化混合项系数
        alpha_ = [0.25, 0.25, 0.25, 0.25]
        for i in range(N):
            if np.random.random(1) < 0.1:  # 生成0-1之间随机数
                X[i, :] = np.random.multivariate_normal(mu1, sigma, 1)  # 用第一个高斯模型生成2维数据
            elif 0.1 <= np.random.random(1) < 0.3:
                X[i, :] = np.random.multivariate_normal(mu2, sigma, 1)  # 用第二个高斯模型生成2维数据
            elif 0.3 <= np.random.random(1) < 0.6:
                X[i, :] = np.random.multivariate_normal(mu3, sigma, 1)  # 用第三个高斯模型生成2维数据
            else:
                X[i, :] = np.random.multivariate_normal(mu4, sigma, 1)  # 用第四个高斯模型生成2维数据
    #   print("可观测数据：\n",X)       #输出可观测样本
    #   print("初始化的mu1，mu2，mu3，mu4：",mu)      #输出初始化的mu

    def e_step(self,sigma, k, N):
        global X
        global mu
        global excep
        global alpha_
        # 遍历每一个样本
        for i in range(N):  # 聚类样本数
            denom = 0
            # 每一个样本进行各聚类类别概率的一个计算
            for j in range(0, k):  # 聚类的类别数  聚成几个类别
                denom += alpha_[j] * math.exp(
                    -(X[i, :] - mu[j, :]) * sigma.I * np.transpose(X[i, :] - mu[j, :])) / np.sqrt(
                    np.linalg.det(sigma))  # 分母
            for j in range(0, k):
                numer = math.exp(-(X[i, :] - mu[j, :]) * sigma.I * np.transpose(X[i, :] - mu[j, :])) / np.sqrt(
                    np.linalg.det(sigma))  # 分子
                excep[i, j] = alpha_[j] * numer / denom  # 求期望
        print("隐藏变量：\n", excep)

    def m_step(self,k, N):
        global excep
        global X
        global alpha_
        for j in range(0, k):
            denom = 0  # 分母
            numer = 0  # 分子
            for i in range(N):
                numer += excep[i, j] * X[i, :]
                denom += excep[i, j]
            mu[j, :] = numer / denom  # 求均值
            alpha_[j] = denom / N  # 求混合项系数

    def main(self):
        iter_num = 6  # 迭代次数
        N = 500  # 样本数目
        k = 4  # 高斯模型数
        probility = np.zeros(N)  # 混合高斯分布
        u1 = [5, 35]
        u2 = [30, 40]
        u3 = [20, 20]
        u4 = [45, 15]
        sigma = np.matrix([[30, 0], [0, 30]])  # 协方差矩阵
        alpha = [0.1, 0.2, 0.3, 0.4]  # 混合项系数
        self.generate_data(sigma, N, u1, u2, u3, u4, alpha)  # 生成数据
        # 迭代计算
        for i in range(iter_num):
            err = 0  # 均值误差
            err_alpha = 0  # 混合项系数误差
            Old_mu = copy.deepcopy(mu)
            Old_alpha = copy.deepcopy(alpha_)
            self.e_step(sigma, k, N)  # E步
            self.m_step(k, N)  # M步
            print("迭代次数:", i + 1)
            print("估计的均值:", mu)
            print("估计的混合项系数:", alpha_)
            for z in range(k):
                err += (abs(Old_mu[z, 0] - mu[z, 0]) + abs(Old_mu[z, 1] - mu[z, 1]))  # 计算误差
                err_alpha += abs(Old_alpha[z] - alpha_[z])
            if (err <= 0.001) and (err_alpha < 0.001):  # 达到精度退出迭代
                print(err, err_alpha)
                break
        # 可视化结果
        # 画生成的原始数据
        plt.subplot(221)
        plt.scatter(X[:, 0].tolist(), X[:, 1].tolist(), c='b', s=25, alpha=0.4,
                    marker='o')  # T散点颜色，s散点大小，alpha透明度，marker散点形状
        plt.title('random generated data')
        # 画分类好的数据
        plt.subplot(222)
        plt.title('classified data through EM')
        order = np.zeros(N)
        color = ['b', 'r', 'k', 'y']
        # 对不同聚类结果的数据进行颜色渲染
        for i in range(N):
            for j in range(k):
                if excep[i, j] == max(excep[i, :]):
                    order[i] = j  # 选出X[i,:]属于第几个高斯模型
                probility[i] += alpha_[int(order[i])] * math.exp(
                    -(X[i, :] - mu[j, :]) * sigma.I * np.transpose(X[i, :] - mu[j, :])) / (
                                        np.sqrt(np.linalg.det(sigma)) * 2 * np.pi)  # 计算混合高斯分布
            plt.scatter(X[i, 0], X[i, 1], c=color[int(order[i])], s=25, alpha=0.4, marker='o')  # 绘制分类后的散点图
        # 绘制三维图像
        ax = plt.subplot(223, projection='3d')
        plt.title('3d view')
        for i in range(N):
            ax.scatter(X[i, 0], X[i, 1], probility[i], c=color[int(order[i])])
        plt.show()



if __name__=='__main__':
    pass

效果应用

import copy
import math
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.colors
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.mixture import GaussianMixture # 高斯混合模型
from sklearn.model_selection import train_test_split

plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = 'False'
class GMM_sklearn():
    def __init__(self):
        pass

    def main(self):
        ## 数据加载
        data = pd.read_csv('../datas/HeightWeight.csv')
        print("数据样本数量:%d, 特征数量:%d" % data.shape)
        x = data[data.columns[1:]]
        y = data[data.columns[0]]
        print(data.head())
        ## 数据分割
        x, x_test, y, y_test = train_test_split(x, y, train_size=0.6, random_state=0)
        ## 模型创建及训练
        gmm = GaussianMixture(n_components=2)  # 聚成2类
        gmm.fit(x, y)
        ## 模型相关参数输出
        print('均值 = \n', gmm.means_)
        print('方差 = \n', gmm.covariances_)
        # 获取预测值
        y_hat = gmm.predict(x)
        y_test_hat = gmm.predict(x_test)

        # 查看一下类别是否需要更改一下
        change = (gmm.means_[0][0] > gmm.means_[1][0])
        if change:
            z = y_hat == 0
            y_hat[z] = 1
            y_hat[~z] = 0
            z = y_test_hat == 0
            y_test_hat[z] = 1
            y_test_hat[~z] = 0

        # 计算准确率
        acc = np.mean(y_hat.ravel() == y.ravel())
        acc_test = np.mean(y_test_hat.ravel() == y_test.ravel())
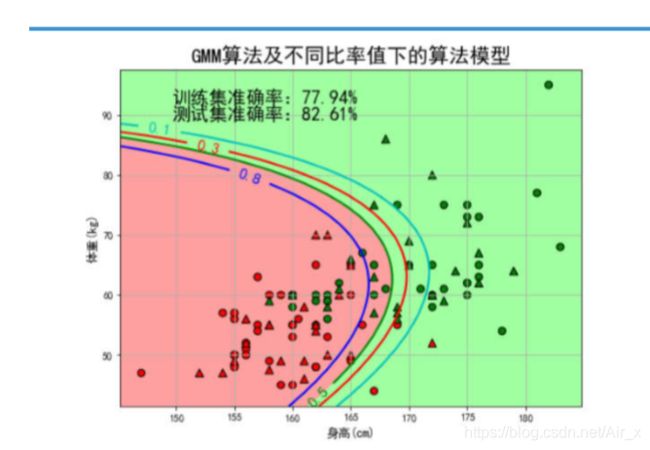
        acc_str = '训练集准确率：%.2f%%' % (acc * 100)
        acc_test_str = '测试集准确率：%.2f%%' % (acc_test * 100)
        print(acc_str)
        print(acc_test_str)
        ## 画图
        cm_light = mpl.colors.ListedColormap(['#FFA0A0', '#A0FFA0'])
        cm_dark = mpl.colors.ListedColormap(['r', 'g'])

        # 获取数据的最大值和最小值
        x1_min, x2_min = np.min(x)
        x1_max, x2_max = np.max(x)
        x1_d = (x1_max - x1_min) * 0.05
        x1_min -= x1_d
        x1_max += x1_d
        x2_d = (x2_max - x2_min) * 0.05
        x2_min -= x2_d
        x2_max += x2_d

        # 获取网格预测数据
        x1, x2 = np.mgrid[x1_min:x1_max:400j, x2_min:x2_max:400j]
        grid_test = np.stack((x1.flat, x2.flat), axis=1)
        grid_hat = gmm.predict(grid_test)
        grid_hat = grid_hat.reshape(x1.shape)
        # 如果预测的结果需要进行更改
        if change:
            z = grid_hat == 0
            grid_hat[z] = 1
            grid_hat[~z] = 0

        # 画图开始
        plt.figure(figsize=(8, 6), facecolor='w')

        # 画区域图
        plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)

        # 画点图
        plt.scatter(x[x.columns[0]], x[x.columns[1]], s=50, c=y, marker='o', cmap=cm_dark, edgecolors='k')
        plt.scatter(x_test[x_test.columns[0]], x_test[x_test.columns[1]], s=60, c=y_test, marker='^', cmap=cm_dark,
                    edgecolors='k')

        # 获取预测概率
        aaa = gmm.predict_proba(grid_test)
        print("预测概率:\n", aaa)
        p = aaa[:, 0].reshape(x1.shape)
        # 根据概率画出曲线图（画出不同概率情况下的预测结果值）
        CS = plt.contour(x1, x2, p, levels=(0.1, 0.3, 0.5, 0.8), colors=list('crgb'), linewidths=2)
        plt.clabel(CS, fontsize=15, fmt='%.1f', inline=True)

        # 设置值
        ax1_min, ax1_max, ax2_min, ax2_max = plt.axis()
        xx = 0.9 * ax1_min + 0.1 * ax1_max
        yy = 0.1 * ax2_min + 0.9 * ax2_max
        plt.text(xx, yy, acc_str, fontsize=18)
        yy = 0.15 * ax2_min + 0.85 * ax2_max
        plt.text(xx, yy, acc_test_str, fontsize=18)

        # 设置范围及标签
        plt.xlim((x1_min, x1_max))
        plt.ylim((x2_min, x2_max))
        plt.xlabel(u'身高(cm)', fontsize='large')
        plt.ylabel(u'体重(kg)', fontsize='large')
        plt.title(u'GMM算法及不同比率值下的算法模型', fontsize=20)
        plt.grid()
        plt.show()

   plt.text(xx, yy, acc_test_str, fontsize=18)

        # 设置范围及标签
        plt.xlim((x1_min, x1_max))
        plt.ylim((x2_min, x2_max))
        plt.xlabel(u'身高(cm)', fontsize='large')
        plt.ylabel(u'体重(kg)', fontsize='large')
        plt.title(u'GMM算法及不同比率值下的算法模型', fontsize=20)
        plt.grid()
        plt.show()