无刷电机无感六步方波驱动原理整理以及过零现象产生分析
无刷电机无感六步方波驱动原理整理以及过零现象产生分析
1.序言
近期在琢磨关于无刷电机驱动,发现在谈论无感六步方波驱动时,都只是提及到会有这么一个过零现象,而没有具体分析为什么,根据本人有限的电磁学理论,反而把自己绕糊涂了,找了本关于电机学的书才算整明白,这里记录一下,顺便整理自己理解的。
2.六步方波驱动回顾
首先是六步方波的驱动方式,这个比较基础就不赘述了,就是在同一时刻只有两相绕组通电,一相输入一相输出,第三相悬空,然后以此类推换相6步,分别是U+V-,U+W-,V+W-,V+U-,W+U-,W+V-。最后的效果是一个周期内每一相的导通时间保持120度的电角度,如下图:

而过零点就发生在每一步悬空的那个引脚上。
3.分析
(1)基本理论
首先,需要明确几个概念,一般的我们认为无刷电机和永磁同步电机的区别仅在于电机的反电势,或者是磁场分布。反电势的波形为梯形的我们认为是无刷电机,而反电势为正弦波的被认为是永磁同步电机。然而实际上,由于工艺等问题,无刷电机其磁通难以饱和形成梯形,普遍都是正弦波,因此在控制方式上PMSM和BLDC属于同种。
从下图可以看出,梯形反电势是由正弦反电势的饱和削顶导致的。
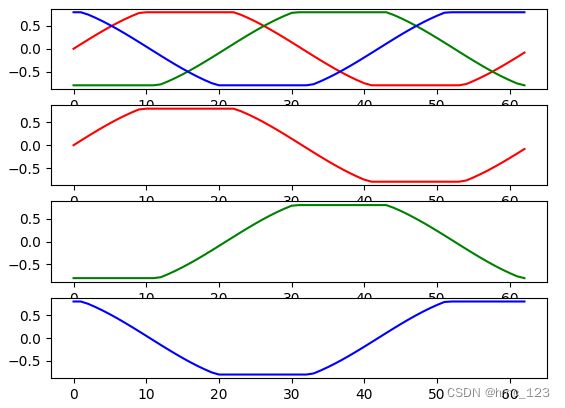

由于三相绕组是互差120度放置的,则转子磁铁两极作为磁场强度H最强的点到达三个绕组的时间差也相差120度,于是在定子绕组内部就产生了三个互差120度且成正弦(余弦)变化的磁场分布以及反电势。
根据感应电动势的公式 E = n Δ ϕ Δ t E=n\frac{\large\Delta\phi}{\large\Delta t} E=nΔtΔϕ我们可以得知,对磁通量求导就是电动势;
而磁场强度H与磁感应强度B之间有 H = B μ 0 H=\frac{B}{\large \mu_0} H=μ0B成正比关系,磁感应强度又与磁通量之间有 ϕ = B ⋅ S \large\phi\normalsize=B\cdot S ϕ=B⋅S;
因此当定子的磁场在绕组上成正弦变化时,它上面的磁通量也成正弦变化,而由磁通量变化形成的感应电动势则成正弦的倒数也即余弦变化的。
(2)换向时刻
再根据六步方波的瞬时磁动势来分析,这里仅仅列举出其中两相的变化。
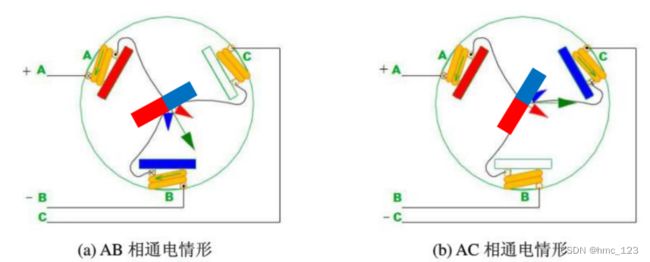
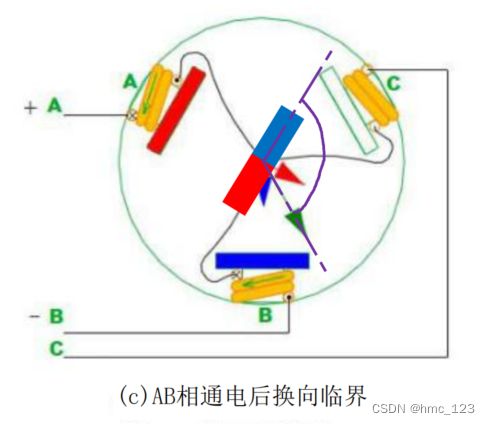
首先看图(a),绿色箭头是电流由A流入,B流出时产生的合成磁矢量。转子保持在上一时刻(C+B-)给定磁场后,转子N极刚刚离开A相时的位置,由于想要转矩最大,需要转子磁极与磁矢量成直角,因此应当在转子的S极对准C相之后产生换向,但是若是在转子S极刚对齐C相时立即换向,想象图a的转子角度时加上图b的磁场,若时机太早可能把转子推回到与B相平行的角度,因此需要等待在图a磁场作用下,转子运动30度,到达图c的位置时,也就是【S极对齐C相之后30度】时产生换向。
因此换相应发生在转子处于比与新的合成磁力线方向垂直的位置不到一点的钝角 (如图c紫色线) 位置,这样可以使产生最大的转矩的垂直位置正好处于本次通电的中间时刻 [ 1 ] ^{\tiny[1]} [1]。
即在图b的角度换向,这样转子转过60度后直到转子与C相平行时才进行下一次换相,扭矩最大时刻正好在AC相通电Step的中间。
(3)无感换向的过零
那么问题顺理成章来了,什么时刻是转子处于与新的合成磁力线方向垂直的时刻呢?从上面的图(a)可以看出,转子的某一磁极对准当前Step中悬空的绕组时,正好与当前新的合成磁力线垂直。
而当转子的磁极对准绕组时,正好也是该绕组上的磁通量最大的时刻,位于正弦信号的两个峰值其中之一,这时在绕组上产生的感应电动势就是对磁通量求导,刚好是0。
下图是无刷电机在一个周期内绕组上的磁场、电压以及电流的波形图 [ 2 ] ^{\tiny[2]} [2]。
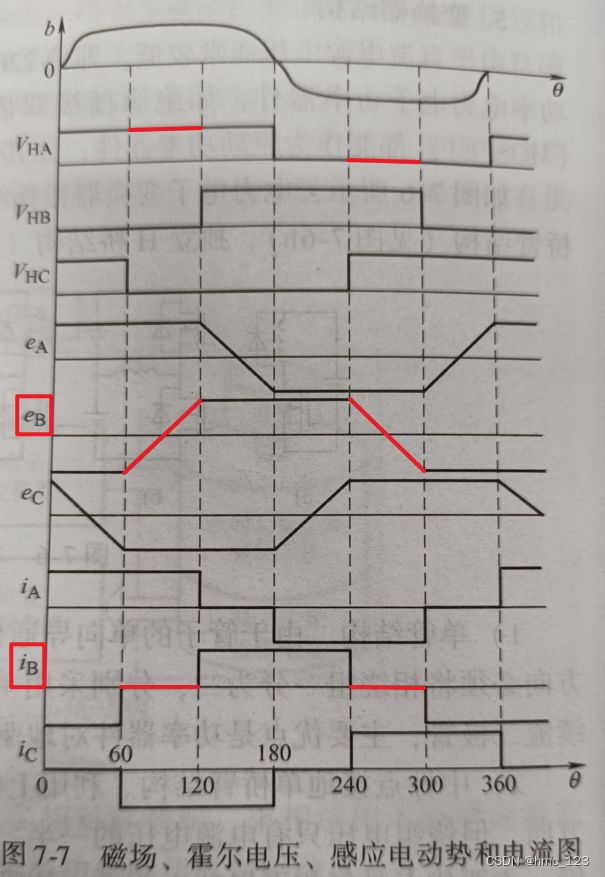
如图所示,当iB为0时,说明B相悬空,应对B相进行反电势采集。其绕组上反电势如图中eB,此时B相上的磁场强度达到峰值,磁通变化率由于逐渐的减小,感应电动势缓慢由负电压持续“下降”(负电压的下降即为上升),直到感应电动势到达反向电压的一个峰值但是被削顶,而后循环往复,于是出现了图中的波形。
即,过零现象刚好发生在当磁极对准悬空相时,那么当悬空相使用各种方法检测到过零发生时,只要延迟30度,等待转子转过“死点”时进行换向,就能保证电机的持续运行。
由于并不是任意时刻的磁电势都能与转子垂直,而是在其最大转矩的前后30度的空间内,因此方波驱动的转矩不恒定,会呈现近似锯齿波的形式。
结束语
以上全凭个人主观推论,若有错误,还望在评论区进行指正。
参考文献:
[1] 无感无刷直流电机之电调设计全攻略 第5页。
[2]电机学 谢宝昌 机械工业出版社 第302页。