首先生成一个线性不可分数据集
import numpy as np
import matplotlib.pyplot as plt
N = 200
x1 = np.linspace(-1, 1, N) # (1, 100)
y1 = x1 ** 2 + 0.2 * np.random.rand(N) # (1, 100)
x1 = np.reshape(x1, (N, 1)) # (100, 1)
y1 = np.reshape(y1, (N, 1)) # (100, 1)
x_c1 = np.concatenate((x1, y1), 1) # (100, 2)
x2 = np.linspace(0, 2, N)
y2 = -(x2 - 1) ** 2 + 0.2 * np.random.rand(N) + 1.5
x2 = np.reshape(x2, (N, 1))
y2 = np.reshape(y2, (N, 1))
x_c2 = np.concatenate((x2, y2), 1) # (100, 2)
data_x = np.concatenate((x_c1, x_c2), 0) # (200, 2)
y_c1 = np.zeros((N, 1)) # (100, 1)
y_c2 = np.ones((N, 1)) # (100, 1)
data_y = np.concatenate((y_c1, y_c2), 0) # (200, 1)
plt.scatter(x1, y1)
plt.scatter(x2, y2)
plt.show()
图像如下
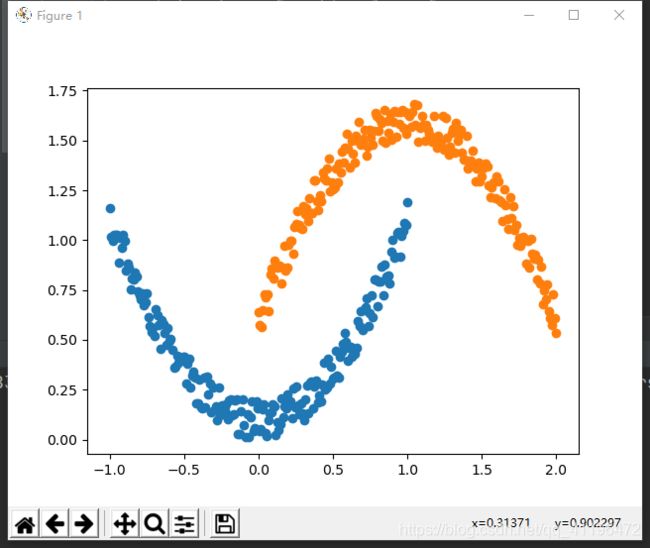
接着搭建网络
import torch.nn as nn
import torch
import torch.utils.data as d
import torch.nn.functional as func
tensor_x = torch.tensor(data_x, dtype=torch.float)
tensor_y = torch.tensor(data_y, dtype=torch.float)
print(tensor_y)
# tensor_x=data, tensor_y=label
data_set = d.TensorDataset(tensor_x, tensor_y)
# shuffle:是否打乱顺序
loader = d.DataLoader(
dataset=data_set,
batch_size=10,
shuffle=True
)
class Net(nn.Module):
def __init__(self):
super().__init__()
self.hidden1 = nn.Linear(2, 32)
self.hidden2 = nn.Linear(32, 16)
self.hidden3 = nn.Linear(16, 1)
def forward(self, x):
x = func.relu(self.hidden1(x))
x = func.relu(self.hidden2(x))
x = func.relu(self.hidden3(x))
return x
net1 = Net()
print(net1)
optimizer = torch.optim.Adam(net1.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()
loss_list = []
网络计算图如下
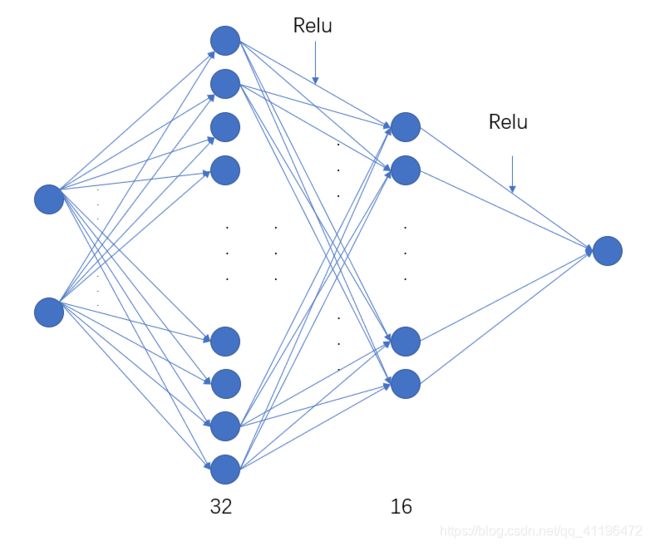
接下来进行训练
# training ...
for epoch in range(100):
for step, (batch_x, batch_y) in enumerate(loader):
prediction = net1(batch_x)
loss = loss_func(prediction, batch_y)
loss_list.append(loss.data.tolist())
optimizer.zero_grad()
loss.backward()
optimizer.step()
训练结果如下

可见收敛了,可以把权值导出来可视化
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import pickle
def relu(a):
return np.maximum(a, 0)
def fun(a, b):
c = np.array([[a],
[b]])
r1 = relu(w1.dot(c) + b1)
r2 = relu(w2.dot(r1) + b2)
r3 = relu(w3.dot(r2) + b3)
return r3
fig = plt.figure()
ax = Axes3D(fig)
x = np.arange(-1, 2, 0.1)
y = np.arange(-1, 2, 0.1)
X, Y = np.meshgrid(x, y)
N = X.shape[0]
Z = np.zeros((N, N))
for i in range(N):
for j in range(N):
Z[i][j] = fun(X[i][j], Y[i][j])
x1 = data_x[:, 0]
y1 = data_x[:, 1]
z1 = data_y
ax.scatter(x1, y1, c='w')
plt.xlabel('x')
plt.ylabel('y')
# ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
ax.contourf(X, Y, Z, zdir='z', offset=0, cmap='rainbow')
ax.set_zlim(0, 1)
plt.show()
首先我们来看网络函数图像和数据点的关系
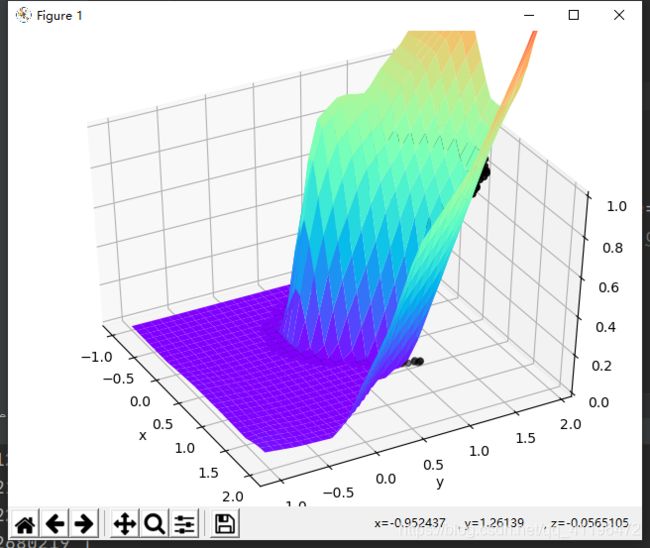
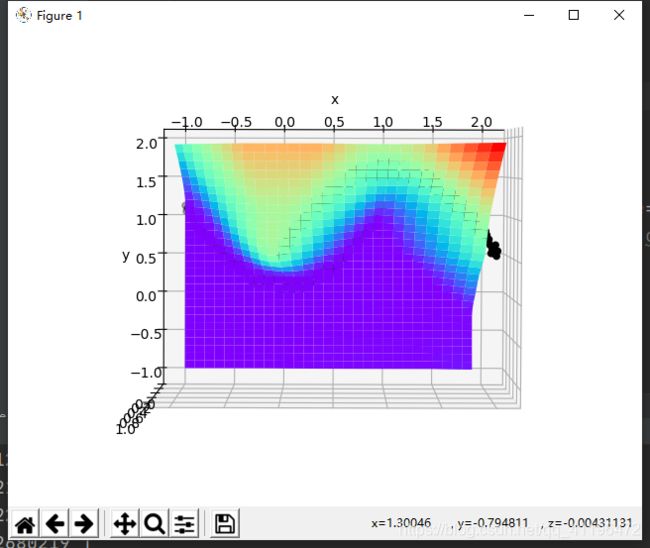
可见函数很好的拟合了数据点
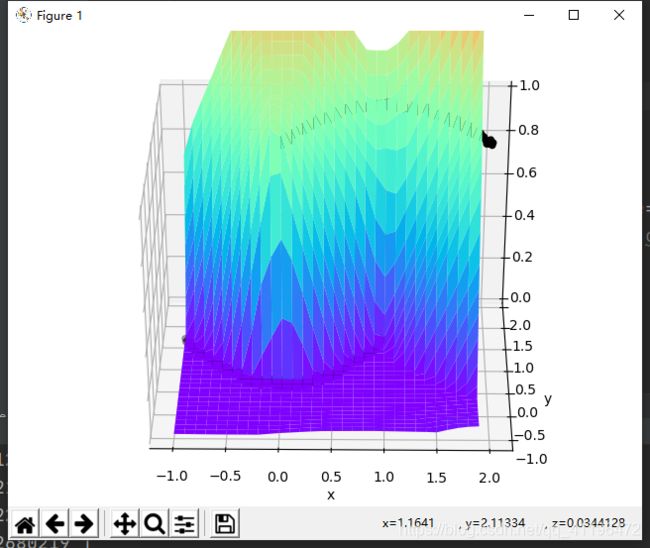
加下了我们来看下投影图
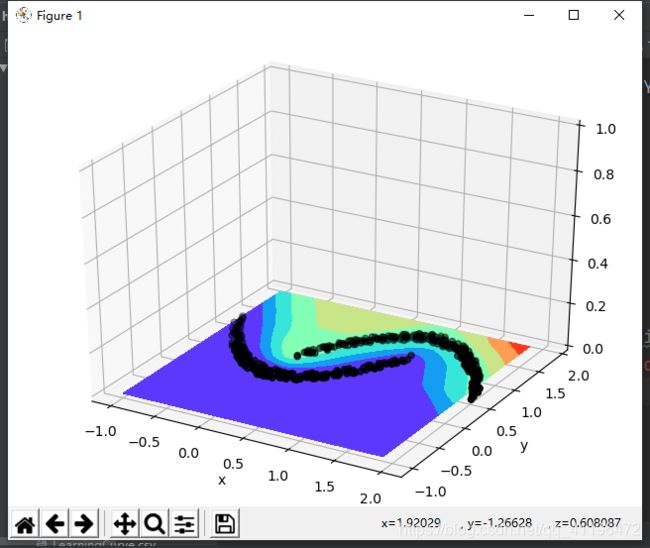
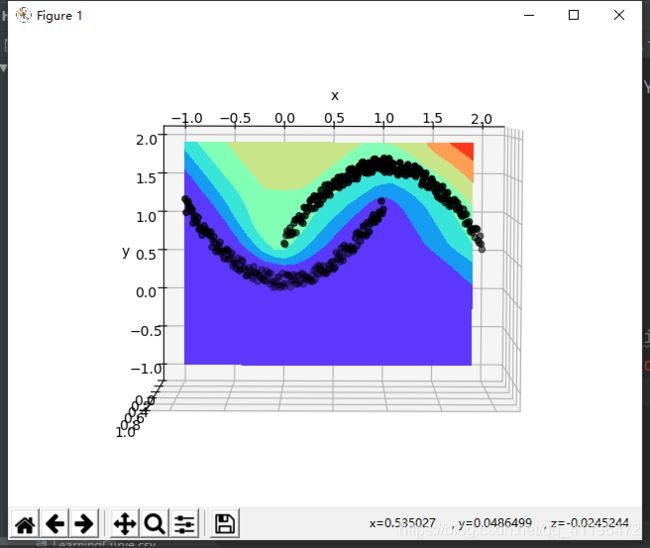
同样可知神经网络对这个非线性可分问题做出了较好的分类







