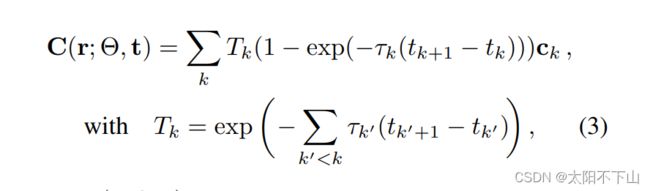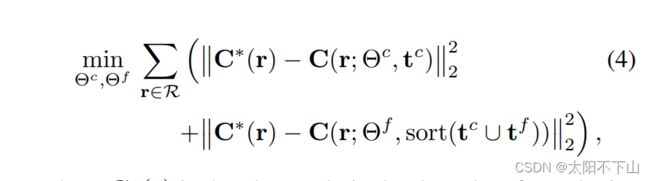【计算机视觉】Mip-nerf 论文精读记录
【计算机视觉】Mip-nerf 论文精读记录
本人是刚入门的计算机视觉小白,此系列为nerf论文精读系列笔记记录,感兴趣的朋友可以关注一下,共同成长!
Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields (ICCV 2021 最佳论文荣誉奖) 抗锯齿神经辐射场的多尺度表示
官方页面:https://jonbarron.info/mipnerf/S
论文链接:https://arxiv.org/abs/2103.13415
开源代码:https://github.com/google/mipnerf

Abstract
神经辐射场(NeRF)使用的渲染程序对每像素有单条射线的场景进行采样,因此,当训练或测试图像观察不同分辨率的场景内容时,可能会产生过于模糊或失真的渲染。对于NeRF来说,通过每像素渲染多条射线来实现超采样的直接解决方案是不切实际的,因为渲染每条射线需要查询一个多层感知器数百次。我们的解决方案,我们称之为“mip-NeRF”(阿拉伯语“mipmap”),扩展了NeRF,以连续值尺度表示场景。通过有效地渲染抗锯齿的锥形圆台 anti-aliased conical frustums而不是射线,mip-NeRF减少了令人反感的锯齿伪影,并显著提高了NeRF表示细节的能力,同时也比NeRF快7%,and是尺寸的一半。与NeRF相比,mip-NeRF在NeRF提供的数据集上的平均错误率降低了17%,在我们提供的数据集上的平均错误率降低了60%。Mip-NeRF也能够在我们的多尺度数据集上匹配蛮力超采样NeRF brute-force supersampled NeRF的精度,同时速度快22×。
Introduction(介绍)
尽管NeRF及其变体在一系列视图合成任务中显示出令人印象深刻的结果,但NeRF的渲染模型在某方面存在缺陷,可能导致过度的模糊和混叠excessive blurring and aliasing。NeRF用连续的体积函数取代了传统的离散采样几何,参数化为多层感知器(MLP),从输入的5D坐标(3D位置和2D观看方向)映射到该位置的场景属性(体积密度和视图相关的发射辐射emitted radiance)。为了渲染一个像素的颜色,NeRF将一条光线通过该像素并输出到其体积表示中,查询沿该射线样本的场景属性的MLP,并将这些值合成成单一颜色。
当所有的训练和测试图像都从大致恒定的距离观察场景内容时,这种方法效果很好(在NeRF和大多数后续实验中,这种方法这样做),但NeRF渲染在不那么设计的场景中显示出显著的伪影。当训练图像以多个分辨率观察场景内容时,恢复的NeRF的渲染在近距离视图中显得过于模糊,并且在远处视图中包含混叠伪影。一个简单的解决方案是采用离线光线追踪中使用的策略:通过使多个光线通过其足迹,对每个像素进行超采样。但对于像NeRF这样的神经体积表示来说,这是非常昂贵的,它需要数百个MLP评估来渲染单条射线,而需要几个小时来重建单个场景。
在本文中,我们从用于防止计算机图形化管道中的混叠的混合映射方法中获得灵感。mipmap表示在一组不同的离散降采样尺度下的信号(通常是图像或纹理map),并根据像素足迹pixel footprint在与该光线相交的几何图形上的投影选择适当的尺度。这种策略被称为预过滤 pre-filtering,,因为抗锯齿的计算负担从渲染时间(如在强力超采样解决方案中)转移到预计算阶段——对于给定的纹理,只需要为mipmap创建一次,无论该纹理被渲染多少次。

图1:NeRF(a)采样点x沿光线,从投影中心到每个像素,然后用位置编码(PE)γ对这些点进行编码,产生一个特征γ(x)。Mip-NeRF (b)则用相机像素定义的三维圆锥截锥进行推理。这些圆锥截锥然后用我们的积分位置编码(IPE)进行特征化,它的工作原理是用多元高斯逼近截锥,然后计算(封闭形式)的积分E[γ(x)]在高斯坐标的位置编码。
我们的解决方案,我们称之为mip-NeRF (multum in parvo NeRF,如“mipmap”),扩展了NeRF,以同时表示连续尺度空间的预过滤辐射场。mip-NeRF的输入是一个三维高斯函数,表示辐亮度场应该积分的区域。如图1所示,我们可以通过沿锥间隔查询mip-NeRF来渲染预过滤的像素,使用近似于像素对应的锥形截锥的高斯函数。为了对三维位置及其周围的高斯区域进行编码,我们提出了一种新的特征表示:集成位置编码(IPE)。这是NeRF位置编码(PE)的一种泛化,它允许空间区域的紧凑特征化,而不是空间中的单个点。
Mip-NeRF大大提高了NeRF的准确性,这种好处甚至更大的情况下,场景内容观察在不同的分辨率(即设置相机移动近或远的场景)。在我们提出的具有挑战性的多分辨率基准测试中,mip-NeRF能够相对于NeRF平均降低60%的错误率(见图2)。Mip-NeRF的尺度感知结构还允许我们将NeRF用于分层采样[30]的单独的“粗”和“细”MLP合并到单个MLP中。因此,mip-NeRF略快于NeRF(~ 7%),并且相比NeRF只有一半的参数。
图2:(a顶部)在全分辨率图像上训练的NeRF能够在新的视图位置上生成逼真的渲染图,但只能在训练图像的分辨率或规模上。(a底部)将相机拉回并放大(或类似地,调整相机的位置以降低图像分辨率)会导致渲染显示出严重的混叠。(b)在多分辨率图像上训练NeRF可以稍微改善这个问题,但会导致跨尺度的渲染质量较差:在全分辨率时模糊,在低分辨率时“锯齿状”。(c)Mip-NeRF也接受了多分辨率图像的训练,能够在不同的尺度上生成逼真的渲染图。每个图像相对于ground-truth(d)的SSIM被插入,两个尺度的最高SSIM用红色表示。
Related Work(相关工作)
我们的工作直接扩展了NeRF,这是一种非常有影响力的技术,用于从观察到的图像中学习3D场景表示,以合成新颖的逼真视图。在这里,我们回顾了计算机图形学和视图合成所使用的3D表示,包括最近引入的连续神经表示,如NeRF,重点关注采样和混叠。
渲染中的抗锯齿 在计算机图形学渲染算法的发展过程中,采样和混叠是被广泛研究的基本问题。减少混叠工件(“抗锯齿”)通常通过超采样或预滤波来实现。基于超采样的技术在渲染时每个像素投射多个射线,以便采样更接近奈奎斯特频率。这是一种减少混叠的有效策略,但代价昂贵,因为运行时通常随超采样率线性扩展。因此,超采样通常只在离线渲染上下文中使用。相比抽样更多的射线来匹配奈奎斯特射线,基于预滤波的技术使用场景内容的低通滤波版本,以减少渲染场景而不产生混叠所需的奈奎斯特频率。预过滤技术更适合实时渲染,因为经过过滤的场景内容版本可以提前预计算,并且可以根据目标采样率在渲染时使用正确的“比例”。在渲染的背景下,预过滤可以被认为是通过每个像素跟踪一个锥而不是一条射线:只要锥与场景内容相交,就会按照锥的足迹对应的比例查询预先计算的场景内容的多尺度表示(如稀疏体素八树或mipmap)。
我们的工作从这条图形线的工作中获得灵感,并为NeRF提供了一个多尺度的场景表示。我们的策略与传统图形管道中使用的多尺度表示在两个关键方面有所不同。首先,我们不能预先计算多尺度表示,因为在我们的问题设置中,场景的几何形状是不知道的——我们正在使用计算机视觉恢复场景的模型,而不是渲染预定义的CGI资产。因此,Mip-NeRF必须在训练中学习预先过滤的场景表示。第二,我们对尺度的观念是连续而不是离散的。Mip-NeRF不是使用固定比例的多个副本来表示场景(就像在mipmap中),而是学习一个可以在任意比例下查询的单一神经场景模型。
视图合成的场景表示 各种场景表示已经被提出用于视图合成的任务:使用观察到的场景图像来恢复一种表示,支持从未观察到的摄像机视点渲染新的逼真的场景图像。当场景的图像被密集捕获时,光场插值技术可用于渲染新的视图,而无需重建场景的中间表示。与采样和混叠相关的问题已经在这个设置中得到了彻底的研究。
从少量捕获的图像中合成新视图的方法通常重建场景的3D几何和外观的明确表示。许多经典的视图合成算法使用基于网格的表示以及漫或视图相关的纹理。基于网格的表示可以有效地存储,并且自然地与现有的图形渲染管道兼容。然而,使用基于梯度的方法优化网格几何和拓扑结构通常是困难的,因为不连续和局部极小。早期的方法使用观察到的图像[37]直接为体素网格着色,而最近的体积方法使用基于梯度的学习训练深度网络来预测场景的体素网格表示。基于离散体素的表示对于视图合成是有效的,但它们不能很好地缩放到高分辨率的场景。
在计算机视觉和图形学研究中,最近的一个趋势是用基于坐标的神经表示取代这些离散表示,它将3D场景表示为连续函数,由从3D坐标映射到该位置的场景属性的mlp参数化。最近的一些方法使用基于坐标的神经表示将场景建模为隐式曲面,但最近的大多数视图合成方法都是基于体积NeRF表示。NeRF启发了许多后续的工作,这些工作将其连续神经体积表示扩展到生成建模、动态场景、非刚性变形物体、具有变化照明和遮挡器的光旅游设置以及用于再照明的反射率建模。
在使用基于坐标的神经表示的视图合成的背景下,采样和混叠的问题相对较少被关注。用于视图合成的离散表示,如多边形网格和体素网格,可以使用传统的多尺度预过滤方法有效地渲染而不产生混叠,比如mipmap和八叉树。然而,基于坐标的神经表示用于视图合成目前只能使用超采样抗锯齿,这加剧了本已缓慢的渲染过程。Takikawa等人最近的工作提出了一种基于稀疏体素八树的多尺度表示方法,用于隐式曲面的连续神经表示,但他们的方法要求场景几何是先验的,这与我们的视图合成设置相反,在视图合成设置中,唯一的输入是观察到的图像。Mip-NeRF解决了这个开放问题,支持在训练和测试期间高效渲染抗锯齿图像,以及在训练期间使用多尺度图像。
2.1 预先知识:NeRF
NeRF使用多层感知器(MLP)的权重将场景表示为一个连续的粒子体积场,这些粒子阻塞并发光。NeRF渲染相机的每个像素如下:射线r(t) = o + td从相机的投影中心o沿d方向发射,从而穿过像素。采样策略用于确定摄像机预定义的近面和远面tn和tf之间的排序距离向量t。对于每个距离tk∈t,我们计算其沿射线x = r(tk)的对应3D位置,然后使用位置编码对每个位置进行转换:
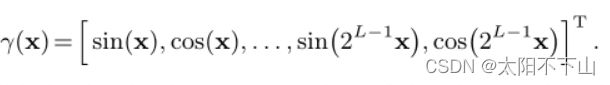
这只是将三维位置x的每个维度的正弦和余弦按2的幂从1缩放到2L−1的拼接,其中L是一个超参数。NeRF的保真度关键取决于位置编码的使用,因为它允许MLP参数化场景作为插值函数,其中L决定插值内核的带宽。每个射线位置的位置编码γ(r(tk))被提供为一个由权重Θ参数化的MLP的输入,该MLP输出一个密度τ和一个RGB颜色c:
MLP还将视图方向作为输入,为了简单起见,在符号中省略了这一点。这些估计的密度和颜色用于使用数值求积来近似体绘制积分,如下:
其中C (r;Θ,t)为像素的最终预测颜色。
在呈现由Θ参数化的NeRF的这个过程中,训练NeRF是简单的:使用已知相机姿态的观察图像,我们使用梯度下降将所有输入像素值和所有预测像素值之间的差平方和最小化。为了提高样本效率,NeRF训练了两个独立的mlp,一个“粗”一个“细”,参数为Θc和Θf:
其中C * ®是从输入图像中提取的观察到的像素颜色,r是所有图像上的所有像素/射线的集合。Mildenhall等人通过分层抽样64个均匀间距随机t值来构建tc。由“粗”模型生成的综合权重
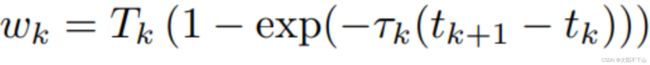
作为描述可见场景内容分布的分段常数PDF。128个新的t值从该PDF使用反变换采样产生tf。然后对这192t值的联合进行排序并传递给“精细”MLP以产生最终的预测像素颜色。
Method(方法)
正如前面所讨论的,NeRF的点采样使它容易受到采样和混叠相关问题的影响:尽管像素的颜色是像素截锥内所有入射亮度的综合,但NeRF每个像素只投射一个极小的窄射线,导致混叠。Mip-NeRF通过从每个像素转换一个圆锥来改善这个问题。我们不是沿着每条射线进行点采样,而是将被铸造的锥分成一系列的锥形锥体(锥体垂直于它们的轴线切割)。与从空间中极小的点构建位置编码(PE)特征不同,我们构建了每个锥形截锥覆盖的体积的集成位置编码(IPE)表示。这些变化使MLP能够推断出每个锥形截锥的大小和形状,而不仅仅是它的质心。由于NeRF对比例不敏感而产生的模糊性以及mip-NeRF对这个问题的解决方案如图3所示。这种锥形截锥和IPE特性的使用还允许我们将NeRF的两个独立的“粗”和“细”MLP减少为一个单一的多尺度MLP,这提高了训练和评估速度,并减少了50%的模型大小。
3.1 圆锥跟踪和位置编码
在这里,我们描述mip-NeRF的渲染和特征化过程,其中我们铸造一个锥,并沿着那个圆锥体设计圆锥形截锥。和在NeRF中一样,mipNeRF中的图像每次呈现一个像素,因此我们可以根据单个感兴趣的像素来描述我们的过程。对于该像素,我们从相机的投影中心o沿着通过像素中心的方向d投出一个圆锥体。该锥体的顶点位于o,在像平面o + d上的锥体半径被参数化为˙r。我们设˙r为世界坐标中像素的宽度乘以2/√12,这就产生了一个锥,它在图像平面上的截面在x和y上的方差与像素足迹的方差相匹配。位于圆锥截锥内两个t值[t0, t1]之间的位置x集合(如图1所示)为:
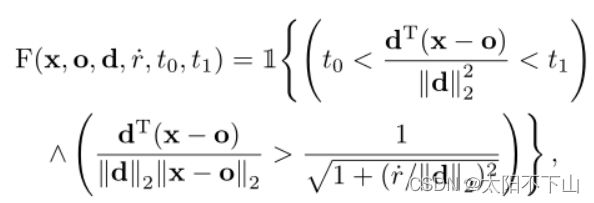
其中1{·}是一个指示函数:F(x,·)= 1 iff x在由(o, d,˙r, t0, t1)定义的圆锥截体内。
我们现在必须构造一个圆锥截锥内部体积的特征表示。理想情况下,这种特征表示形式应该与NeRF中使用的位置编码特征类似,因为Mildenhall等人表明,这种特征表示对NeRF的成功至关重要。对此有许多可行的方法(详见附录),但我们发现的最简单、最有效的解决方案是简单地计算锥体截锥内所有坐标的期望位置编码:
然而,目前还不清楚如何有效地计算这样的特征,因为分子中的积分没有封闭形式的解。因此,我们用多元高斯近似圆锥截锥,这允许对所需特征的有效近似,我们称之为“集成位置编码”(IPE)。
为了近似具有多元高斯的圆锥截锥,我们必须计算F(x,·)的均值和协方差。因为假设每个锥形截锥都是圆形的,而且由于锥形截锥围绕锥轴对称,这样的高斯分布由三个值(除了o和d)完全表征: 沿射线的平均距离(µt),沿射线的方差(σ2t),垂直于射线的方差(σ2r):
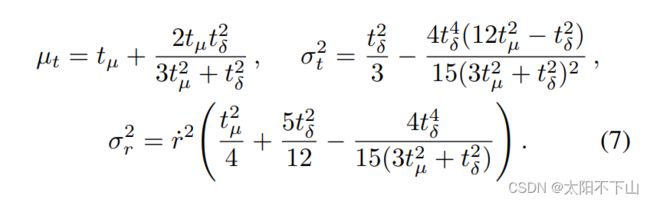
这些量是根据中点tµ= (t0 + t1)/2和半宽度tδ = (t1−t0)/2参数化的,这对数值稳定性至关重要。详细推导请参考附录。我们可以把这个高斯从圆锥截锥的坐标系变换成世界坐标如下:
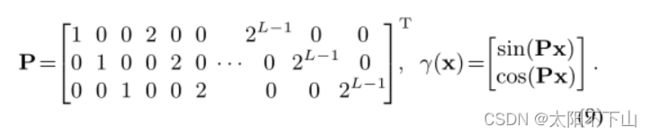
这种重新参数化使我们可以为IPE推导出一个封闭的形式。利用变量线性变换的协方差是变量协方差的线性变换这一事实(Cov[Ax, By] = a Cov[x, y]BT) 我们可以确定圆锥截锥高斯在被提升到PE基P后的均值和协方差:
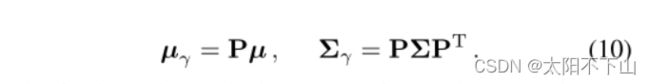
生成IPE特征的最后一步是计算这个提升的多元高斯函数的期望,由位置的正弦和余弦调制。这些期望有简单的封闭形式表达式:
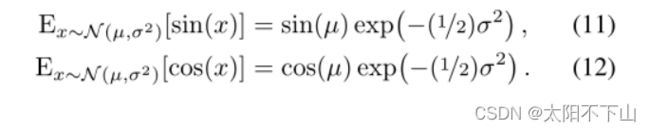
我们看到这个期望的正弦或余弦仅仅是由方差的高斯函数衰减的平均值的正弦或余弦。有了这个,我们可以计算我们的最终IPE特征作为期望的正弦和余弦的平均值和协方差矩阵的对角线:
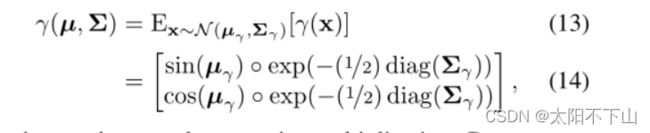
其中◦表示元素的乘法。因为位置编码独立地编码每个维度,这种预期的编码只依赖于γ(x)的边缘分布,并且只需要协方差矩阵的对角线(每个维度的方差向量)。由于Σγ相对较大,计算成本非常高,我们直接计算Σγ的对角线:
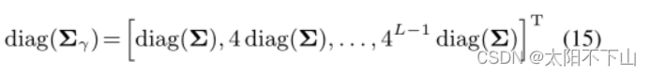
这个向量只依赖于3D位置的协方差Σ的对角线,它可以计算为:
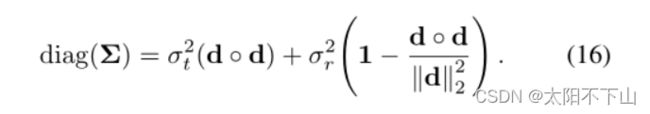
如果直接计算这些对角线,构建IPE特征的成本大致与PE特征相同。
图4显示了在一维领域中IPE和传统PE特征之间的差异。IPE特征表现得很直观:如果位置编码中的某个特定频率的周期大于用于构建IPE特征的区间宽度,那么该频率上的编码不受影响。但如果周期小于间隔(在这种情况下,PE在该间隔上将反复振荡),那么在该频率上的编码将缩小到零。简而言之,IPE保留了在一段时间内恒定的频率,并温和地“删除”了在一段时间内变化的频率,而PE保留了在一些手动调优的超参数L之前的所有频率。通过以这种方式缩放每个正弦和余弦,IPE特征是有效的抗锯齿位置编码特征,平滑地编码空间体积的大小和形状。IPE还有效地去除了L作为超参数:它可以简单地设置为一个非常大的值,然后永远不调优(参见补充)。

图4:NeRF使用的位置编码(PE)的1D可视化(左)和我们的集成位置编码(IPE)(右)。由于NeRF采样点沿着每条射线,并对所有频率进行相同的编码,高频PE特征被混淆,这导致渲染伪影。通过在每个区间上集成PE特征,当频率的周期比被集成的区间小时,IPE特征的高频维度收缩为零,从而产生反锯齿特征,隐式编码区间的大小(在更高的维度上,形状)。
3.2. 结构
除了圆锥跟踪和IPE特性,mip-NeRF的行为类似于NeRF,如2.1节所述。对于每个被渲染的像素,而不是像NeRF中那样是一个射线,而是一个锥。我们不是沿着射线对tk采样n个值,而是对tk采样n + 1个值,计算每个相邻的采样tk值对的间隔的IPE特征,如前所述。这些IPE特征作为输入传入MLP以产生密度τk和颜色ck,如公式2所示。mip-NeRF中的渲染遵循式3。
回想一下,NeRF使用了具有两个不同mlp的分层抽样程序,一个是“粗的”,一个是“细的”(参见公式4)。这在NeRF中是必要的,因为它的PE特征意味着它的mlp只能学习一个单一比例的场景模型。但是我们的锥形铸造和IPE特性允许我们显式地将尺度编码到我们的输入特征中,从而使MLP能够学习场景的多尺度表示。因此,Mip-NeRF使用一个带参数Θ的MLP,我们在分层抽样策略中重复查询该参数。这样做有多个好处:模型大小减半,渲染更精确,采样更有效,整体算法更简单。我们的优化问题是:

因为我们只有一个MLP,“粗”损耗必须与“细”损耗相平衡,这是通过一个超参数λ(我们在所有实验中设置λ = 0.1)来实现的。与Mildenhall等人[30]一样,我们的粗样本tc是通过分层抽样产生的,而我们的细样本tf是从使用反变换抽样得到的alpha合成权重w中抽样产生的。与NeRF不同,在NeRF中,精细MLP是64个粗样本和128个精细样本的排序并集, 在mip-NeRF中,我们只需从粗模型中抽取128个样本,从细模型中抽取128个样本。模型(产生与NeRF相同的MLP总评估数 与NeRF中相同,以便进行公平的比较)。在对tf采样之前,我们稍微修改权重w:
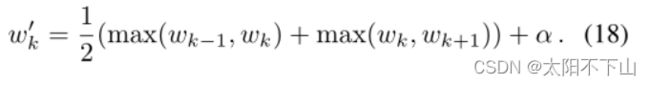
我们用一个2头的最大滤波器和一个2头的模糊滤波器(一个 “模糊池”)过滤权重w,在w上产生了一个宽而光滑的上包络。在包络线被重新归一化为和为1之前,在包络线中添加一个超参数α,这确保了一些样本即使在空区域也能被绘制(我们在所有实验中设置α = 0.01)。
Mip-NeRF是在JaxNeRF[11]之上实现的,JaxNeRF[11]是NeRF的JAX[4]重实现,实现了更好的精度和比原始TensorFlow实现更快的训练。我们遵循NeRF的训练程序:100万次Adam迭代,批大小为4096,学习率对数退火从5·10−4到5·10−6。有关JaxNeRF和mip-NeRF之间的其他细节和其他差异,请参阅补充部分,这些差异对性能影响不大,是我们的主要贡献(锥跟踪、IPE和单一多尺度MLP的使用)的附带内容。
Results(结果)
我们在原始NeRF论文[30]中提出的Blender数据集上评估mip-NeRF,也在该数据集的一个简单的多尺度变量上进行评估,该数据集旨在更好地探测多分辨率场景的准确性,并突出NeRF在此类任务中的关键漏洞。我们报告了NeRF使用的三个错误指标:PSNR, SSIM和LPIPS。为了便于比较,我们还提出了一个总结所有三个指标的“平均”误差指标: 几何平均值 ![]()
以及LPIPS。此外,我们还报告了运行时(壁时间的中位数和绝对偏差的中位数)以及NeRF和mip-NeRF每种变体的网络参数数量。所有JaxNeRF和mip-NeRF实验都在32核TPU v2[17]上进行训练。
我们构建了我们的多尺度Blender基准测试,因为NeRF使用的原始Blender数据集有一个微妙但关键的弱点:所有相机都有相同的焦距和分辨率,并且与物体的距离相同。因此,这个Blender任务比大多数现实世界的数据集要容易得多,在现实世界中,相机可能离被摄物更近或更远,也可能放大或缩小。该数据集的局限性被NeRF的局限性所补充:尽管NeRF倾向于产生别名渲染,但它能够在Blender数据集上产生出色的结果,因为该数据集系统地避免了这种失败模式。
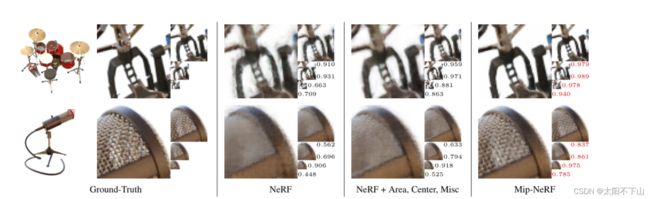
图5:mip-NeRF输出的可视化结果与ground-truth、NeRF和NeRF的改进版本在我们的多尺度Blender数据集中的两个场景的测试集图像上的对比。我们将这两个场景在4个不同尺度下的裁剪区域可视化,显示为一个图像金字塔,每个尺度的SSIM显示在右下方,每个尺度的最高SSIM用红色突出显示。Mip-NeRF在视觉和数量上都明显优于NeRF及其改进版本。有关更多这样的可视化,请参阅补充部分。

表1:mip-NeRF及其消融与NeRF和我们的多尺度Blender数据集测试集上的几个NeRF变体的定量比较。详情见正文。
多尺度Blender数据集 我们的多尺度Blender数据集是对NeRF Blender数据集的直接修改,设计用于探测混叠和尺度空间推理。这个数据集是这样构造的:取Blender数据集中的每个图像,对其进行2、4和8的下采样(并相应地修改相机的intrinsic),并将原始图像和三张下采样的图像合并到一个数据集中。由于射影几何的性质,这类似于重新渲染原始数据集,其中到相机的距离被增加了2、4和8的比例因子。在这个数据集上训练mipNeRF时,我们将每个像素的损失按原始图像中该像素占用的面积进行缩放(来自1/4图像的像素损失按16缩放,等等),以便少数低分辨率像素与许多高分辨率像素具有相当的影响。此任务的平均误差度量使用所有四个尺度上每个误差度量的算术平均值。
mip-NeRF对这个多尺度数据集的性能如表1所示。因为NeRF是Blender数据集上最先进的技术(如表2所示),我们只针对NeRF和NeRF的几个改进版本进行评估:“面积损失”增加了上述损失函数按mip-NeRF使用的像素面积的缩放,“居中像素”在每个射线的方向上增加了一个半像素的偏移量,这样射线就可以通过每个像素的中心(与Mildenhall等人所做的每个像素的角落相反) “Misc”增加了一些小的改变,略微提高了训练的稳定性(见补充)。
Mip-NeRF在这项任务中减少了60%的平均错误,并且在所有指标和所有尺度上都比NeRF表现更好。“定心”像素大大提高了NeRF的性能,但还不足以接近mip-NeRF。去除IPE特征会导致mip-NeRF的性能下降到“集中”NeRF的性能,从而证明锥铸和IPE特征是驱动性能的主要因素(尽管面积损失贡献很大)。
单MLP”mip-NeRF消融性能良好,但其参数是mip-NeRF的两倍,速度比mip-NeRF慢近20%(可能是由于该消融需要对t值进行排序,硬件较差) 由于它的“粗”和“细”尺度上的张量大小的变化)。Mip-NeRF也比NeRF快~ 7%。参见图9和可视化的补充。
Blender 数据集 虽然mipNeRF设计用来解决的采样问题在多尺度Blender数据集中最为突出,但mipNeRF在Mildenhall等人[30]提出的更简单的单尺度Blender数据集上也优于NeRF,如表2所示。我们根据NeRF、NSVF[24]和以前使用的相同的变体和消融(不包括“面积损失”,mip-NeRF在本任务中没有使用它)使用基线进行评估。虽然mip-NeRF没有多尺度Blender数据集那么引人注目,但与NeRF相比,mip-NeRF能够将平均错误减少约17%,同时速度也更快。这种性能改进在具有挑战性的情况下(如小结构或薄结构)最明显,如图6所示。
超采样 正如在介绍中所讨论的,mipNeRF是一种用于抗锯齿的预过滤方法。另一种方法是超采样,它可以在NeRF中通过每个像素投射多个抖动射线来实现。因为我们的多尺度数据集是由全分辨率图像的下采样版本组成的,我们可以通过训练一个NeRF(之前表现最好的 "NeRF + Area, 训练一个只使用全分辨率图像的NeRF(之前表现最好的 "NeRF+区域、中心、杂项 "的变体),然后构建一个 只使用全分辨率的图像,然后只渲染全分辨率的图像。 分辨率的图像,然后我们对这些图像进行手动降采样。这个基线有一个不公平的优势:我们手动删除多尺度数据集中的低分辨率图像,否则会降低NeRF的性能,如前所述。这种策略在大多数现实世界的数据集中是不可用的,因为通常不可能知道a-priori哪些图像对应哪些图像内容的比例。尽管这个基线有优势,mip-NeRF与它的精度相当,而且速度快了约22倍(见表3)。
Conclusion(结论)
我们提出了mip-NeRF,一个多尺度的NeRF类模型,解决了NeRF固有的混叠问题。NeRF的工作原理是投射射线,沿这些射线对点的位置进行编码,并在不同的尺度上训练独立的神经网络。相比之下,mip-NeRF铸造锥,编码锥形锥锥的位置和大小,并训练一个单一的神经网络,在多个尺度下建模场景。通过对采样和尺度的明确推理,mip-NeRF能够在我们自己的多尺度数据集上相对于NeRF减少60%的错误率,在NeRF的单尺度数据集上减少17%,同时也比NeRF快7%。Mip-NeRF也能够匹配蛮力超采样NeRF变体的精度,同时速度快22倍。我们希望这里介绍的一般技术将对其他致力于改进基于光线跟踪的神经渲染模型的性能的研究人员有价值。
论文笔记记录:
Mip来源于拉丁语multum in parvo:放置很多东西的小空间 。在 computer graphics中mipmapping是一种加快渲染速度、减少图像锯齿的贴图渲染技术[4]。简单说,mipmapping就是把主图缩小成一系列依次缩小的小图片,并把这些更低解析度的小图片保存起来。这种策略被称为pre-filtering,抗锯齿的计算负担都集中在预处理上:不论之后需要对一个texture做多少次渲染,都只需要预处理一次即可。
Mip-NeRF提出的背景是:在渲染过程中,如果NeRF在每个pixel用single ray来sample场景,(NeRF在做渲染时)会出现模糊(blurred)和锯齿(aliased)的情况:blurred in close-up views and contain aliasing artifacts in distant views。这种情况通常由于输入的同一个场景对应的多个图片解析度(resolution)不一致而导致的。最简明的解决方法是渲染时每个pixel下用multiple rays。但是对NeRF来说并不现实;因为沿着一条ray渲染就需要querying一个MLP几百次。
Mip-NeRF的解决方案和NeRF有一个本质不同:NeRF渲染是要基于ray的,然而Mip-NeRF是基于conical frustums的,并且是anti-aliased的。最终,Mip-NeRF与NeRF相比具有更快、更小、更准的优势,更加适合处理multiscale的数据。
Mip-NeRF主要贡献有三:
①Cone tracing
②Integrated Positional Encoding (IPE)
③A single multi scale MLP
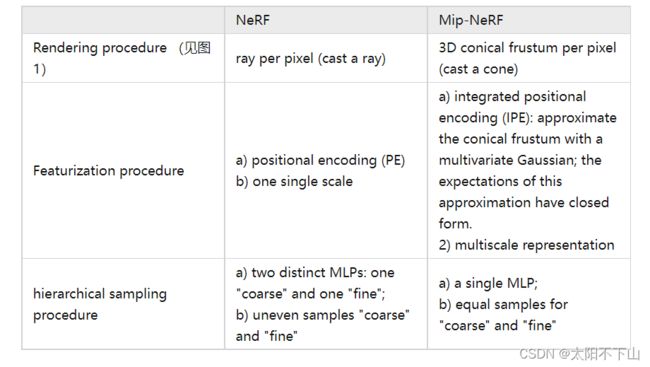
其中,Integrated positional encoding有两个优势:
平滑地encode了一个volume的大小和形状,具有更好的抗锯齿能力,见图2。
考虑了samples的frequencies,降低了带有锯齿PE特征的影响,见图3。
不需要调整普通PE中超参。 PE中有一个隐含假设,即所有样本点都有一样的isotropic covariance matrices,其中的方差项是由超参L决定的;同时,超参 L决定了哪个频率(主要是高频)上的PE特征要剔除。然而在IPE中,这些高频PE特征的影响受限于the size of multivariate Guassion:size越大影响越小,反之亦然。
局限性:见下一篇citynerf~