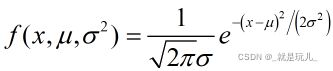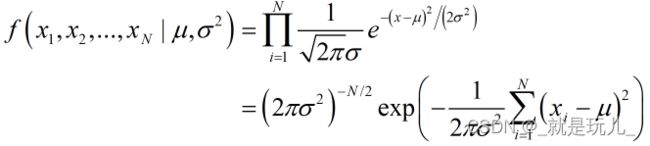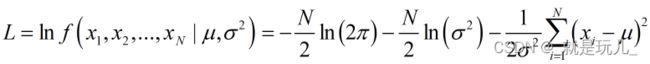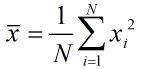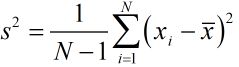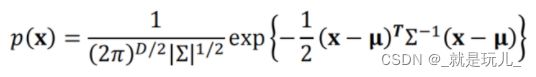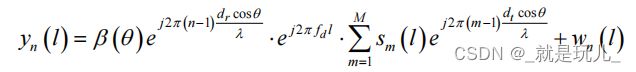MIMO雷达极大似然估计（Maximum Likelihood Estimation Using MIMO Radar）

上学期事情太多，占了很多坑最后都没有填。这学期逐渐步入正轨，尽量把所学所想及时更新。

本文从最大似然估计的基本理论出发，结合MATLAB最后做MIMO雷达ML参数估计。

参考书《现代信号处理（第三版）张贤达著 p35》

最大似然估计基本思想是：在对被估计的未知量没有任何先验知识的情况下，利用已知的若干观测值估计该参数。其中似然函数是包含未知参数信息的可能性（likelihood）。

满足高斯分布的概率密度函数：

似然函数

从而得对数的似然函数形式 

 最大似然函数的约束优化方法如下，同时对数函数又是单调递增的，所以未知参数最大似然估计式如下

求解未知参数的方法可以搜索或者直接求偏导得到

                                   

如果用向量的形式表示似然函数 高斯分布的极大似然估计_Yemiekai的博客-CSDN博客_高斯分布的最大似然估计

对高斯分布的向量形式对数似然函数最大似然估计的约束优化准则为

---

 为了更好理解ML估计，接下来贴一些MATLAB代码，同时MATLAB也有ML估计的函数“mle” 

x = randn(10000,1);
h = histogram(x);   % 分布直方图；统计某个数在整个数的占比是多少，区间为坐标左闭右开的统计
phat = mle(x)

得到如图所示的直方图，输出该分布的均值为0，方差为1

---

如果不用MATLAB自带的函数“mle”，还可以自己按照上述的公式来搜索得到ML估计结果，贴了github上一位老哥的代码，我稍微修改了一下

% Demonstration of Maximum Likelihood Estimation in Matlab
%   Author: Mathuranathan (https://www.gaussianwaves.com)
%   License : creative commons : Attribution-NonCommercial-ShareAlike 3.0 Unported
clc;
close all;
clear;

A=1.3;
N=50; %采样点
x=A+randn(1,N);
s=1; %标准差 s=1 

rangeA=-2:0.0001:5; %搜索范围
L=zeros(1,length(rangeA)); %搜索长度

for i=1:length(rangeA)
    %计算似然函数
    L(i) = exp(-sum((x-rangeA(i)).^2)/(2*s^2));  %忽略常数项
end

[maxL,index]=max(L); %选择极大似然函数的最大值
display('Maximum Likelihood of A');
display(rangeA(index));

%Plotting Commands
figure;
plot(rangeA,L);hold on;
stem(rangeA(index),L(index),'r'); %Point the Maximum Likelihood Estimate
displayText=['\leftarrow Likelihood of A=' num2str(rangeA(index))];
title('Maximum Likelihood Estimation of unknown Parameter A');
xlabel('\leftarrow A');
ylabel('Likelihood');
text(rangeA(index),L(index)/3,displayText,'HorizontalAlignment','left');

figure;
plot(rangeA,log(L));hold on;
YL = ylim;YMIN = YL(1);
plot([rangeA(index) rangeA(index)],[YMIN log(L(index))] ,'r'); %Point the Maximum Likelihood Estimate
title('Log Likelihood Function');
xlabel('\leftarrow A');
ylabel('Log Likelihood');
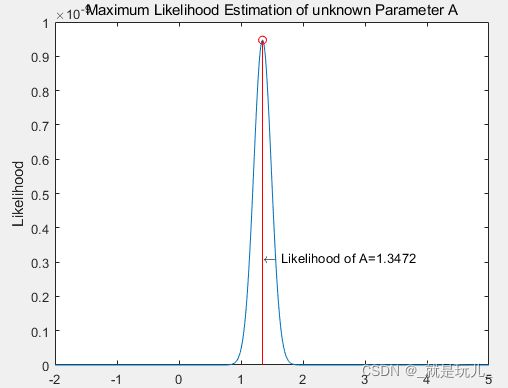
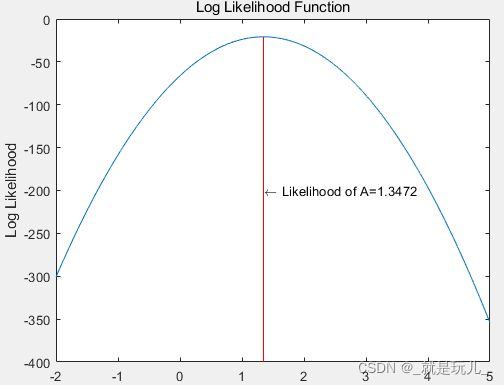
text([rangeA(index)],YMIN/2,displayText,'HorizontalAlignment','left');

得到似然函数和对数似然函数的谱图

            

---

接下来说明一下MIMO雷达极大似然估计处理方法

 参考文献 “[1].Parameter Estimation of Maneuvering Target Using Maximum Likelihood Estimation for MIMO Radar with Colocated Antennas”（主要参考这篇，对该文公式稍做解释）；“[2].MIMO雷达最大似然估计_夏威”；“[3].Maximum Likelihood Methods in Radar Array Signal Processing_Petre Stoica”

MIMO雷达信号模型及其矩阵表示形式

典型的信号模型，具体不做过多介绍，分别包括反射系数，接受阵列方向矢量，多普勒矢量，发射信号，发射方向矢量和高斯白噪声噪声。

接着文章将矩阵构型的回波改成向量的形式：这样可以直接利用前文中的向量似然函数的结果。

估计似然函数中的目标方差，用表示，据文章[3]中式(11)-(14)，设方差的估计值为

 代入上文对数似然函数中可得极大似然函数的优化目标为

 最后一项[1]中推导得其方阵的非对角线元素都为0，所以对优化函数的结果不产生影响，进而可得MIMO雷达ML参数估计可等效于

 贴一下该作者写的代码，我稍作了修改

clear
close all
clear

nT = 8; % 发射阵元
nR = 8; % 接收阵元
L = 181;
M = 101;
theta = linspace(-90,90,L).'*pi/180;
freq = linspace(-0.5,0.5,M).';

% 发送信号模型
N = 100;
X = (sign(randn(nT,N)) + 1j*sign(randn(nT,N)))/sqrt(2);
varn = 1;

% 目标2参数
fd = -0.1;
thetat = -55*pi/180;
d = exp(1j*2*pi*fd*(0:N-1)).';
aT = exp(1j*pi*(0:nT-1)*sin(thetat)).';
aR = exp(1j*pi*(0:nR-1)*sin(thetat)).';
Y = aR*aT.'*X*diag(d);

% 目标2参数
fd = 0.3;
thetat = -55*pi/180;
d = exp(1j*2*pi*fd*(0:N-1)).';
aT = exp(1j*pi*(0:nT-1)*sin(thetat)).';
aR = exp(1j*pi*(0:nR-1)*sin(thetat)).';
Y = Y + aR*aT.'*X*diag(d);

% 高斯噪声
Y = Y + sqrt(varn)*(randn(nR,N) + 1j*randn(nR,N));
y = vec(Y);

% Detection
P = zeros(L,M); % L为遍历的角度索引值，M为遍历的多普勒索引值
for i = 1:L
    aT = exp(1j*pi*(0:nT-1)*sin(theta(i))).';
    aR = exp(1j*pi*(0:nR-1)*sin(theta(i))).';
    A = aR*aT.';
    for k = 1:M
        dk = exp(1j*2*pi*freq(k)*(0:N-1)).';
        vk = vec(A*X*diag(dk));
        P(i,k) = abs(y'*vk + vk'*y) / (2*N*nT*nR);
    end
end

figure;
mesh(freq,theta*180/pi,P)
xlabel('Frequency')
ylabel('DOA (degree)')
zlabel('Post-Correlation Power')
title('Ntx = 8')

 得到最后ML估计的谱图