自回归滑动平均模型ARMA

$ARMA$模型介绍

自回归滑动平均模型（$Auto-RegressiveandMovingAverageModel,ARMA$）是基于自回归模型($AR$)和滑动平均模型（$MA$）的混合模型。

$$\{\begin{array}{rl}& x_t={\phi }_0+\sum _{i=1}^p{\phi }_i{x}_{t-i}+{\epsilon }_t-\sum _{i=1}^q{\theta }_i{\epsilon }_{t-i}\\ & {\phi }_p\ne 0,{\theta }_q\ne 0\\ & E({\epsilon }_t)=0,Var({\epsilon }_t)={\sigma }_{\epsilon }^2,E({\epsilon }_t{\epsilon }_s)=0,s\ne t\\ & E(x_s{\epsilon }_t)=0,\forall s<t\end{array}\text{\hspace{1em}(1)}$$

当样本容量$n$充分大时，样本自相关系数${\hat{\rho }}_k$和样本偏相关系数$\widehat{{\gamma }_k}$近似服从正态分布（证明略）。
$$\begin{array}{r}{\hat{\rho }}_k\sim N(0,\frac{1}{n})\\ \widehat{{\gamma }_k}\sim N(0,\frac{1}{n})\end{array}\text{\hspace{1em}(2)}$$
根据正态分布的性质有：
$$\begin{array}{r}P(|{\hat{\rho }}_k|\le \frac{2}{\sqrt{n}})\ge 0.95\\ P(|\widehat{{\gamma }_k}|\le \frac{2}{\sqrt{n}})\ge 0.95\end{array}\text{\hspace{1em}(3)}$$

定阶原则

$ACF$定阶

如果样本自相关系数再最初的$q$阶明显超过2被标准差范围，而后几乎95%的自相关系数都落在2倍标准差的范围以内，而且由非零自相关性系数衰减到置信区间的过程非常突然，视为自相关系数截尾。结尾阶数即为$MA$的阶数$q$。

如果由超过5%样本自相关系数落入2倍标准差范围值之外，或者由显著非零的自相关系数衰减到置信区间的过程比较缓慢或者非常连续，视为自相关系数拖尾。

同理$PACF$。

MA模型定阶示例

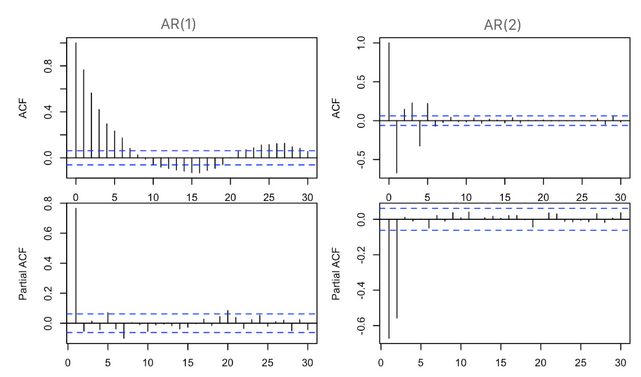
图中蓝色虚线表示2倍标准差的置信区间，对于$MA$模型，偏自相关系数拖尾，自相关系数$q$阶截尾。

---

AR模型定阶示例

对于$AR$模型而言，自相关系数拖尾，偏自相关系数$p$阶截尾。

---

ARMA模型定阶

$ARMA(p,q)$模型自相关系数和偏自相关系数都是拖尾的，阶数无法通过$ACF$和$PACF$图看出。

可以通过定量分析$AIC$准则和$BIC$准则来计算$ARMA$模型的阶数$p,q$

• $AIC$准则(Akaike information Criterion 最小化信息量准则)
  $$AIC=-2ln(L)+2K\text{\hspace{1em}(4)}$$

  • L：表示模型的极大似然函数
  • K：表示模型参数个数
  • 不足：当样本容量很大时，在$AIC$准则中拟合误差提供的信息就要受到样本容量的放大，而参数个数的惩罚因子却和样本容量没有关系（一直是2），因此当样本容量很大时，使用$AIC$准则的模型不收敛于真实模型，它通常比真实模型所含的未知个数要多。

• $BIC$准则(Bayesian information Criterion 贝叶斯信息准则)
  $$BIC=-2ln(L)+Kln(n)\text{\hspace{1em}(5)}$$

  • $n$：样本容量

通过设定$(p,q)$的上限$(p_{max},q_{max})$，遍历$p\in [1,p_{max}],q\in [1,q_{max}]$中的所有整数组合，取其AIC最小或BIC最小时对应的$p,q$为$ARMA$模型的阶数$p^{\ast },q^{\ast }$。

定阶总结

模型	自相关系数	偏自相关系数
$AR(p)$	拖尾	$p$阶截尾
$MA(q)$	$q$阶截尾	拖尾
$ARMA(p,q)$	拖尾	拖尾

图片来源：https://blog.csdn.net/weixin_39982225/article/details/120623005

王燕.应用时间序列分析[M].中国人民大学出版社.201907