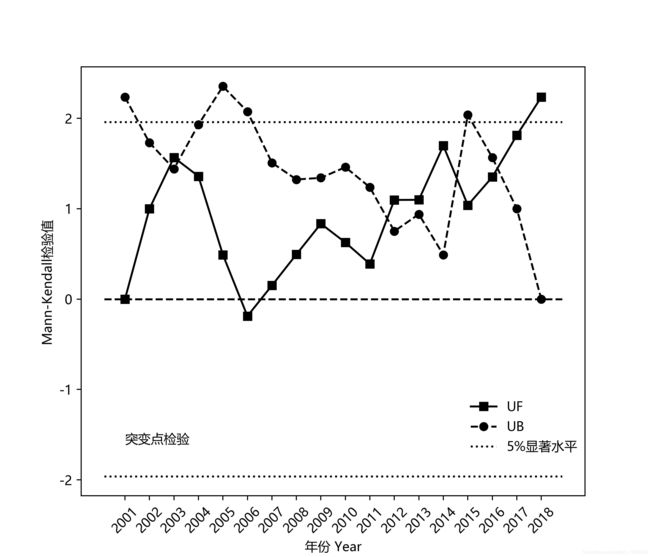
python mk趋势检验的实现

简介

在网上查了很久有关MK突变检验的代码，大部分都是基于matlab实现。由于本人不熟悉matlab，于是将matlab代码转换成了python代码，并最终调试出正确可运行的代码。

20210723
更新了代码，以方便更好控制数据及输出图格式
主要看到有人问参数如何修改，于是今天把代码优化了下，如有不足之处，请指正。
数据下载积分固定在了5.大家有需要自取。

原理

Manner-Kendall(M-K)—突变检验原理

初始代码

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

plt.rcParams['font.family'] = ['MicroSoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

df = pd.read_excel(r'D:\py\data.xls')

# 获取数据
x = df['year']
y = df['data']

n = len(y)

# 正序计算
# 定义累计量序列Sk，长度n，初始值为0
Sk = np.zeros(n)
UFk = np.zeros(n)

# 定义Sk序列元素s
s = 0

for i in range(1, n):
    for j in range(0,i):
        if y.iloc[i] > y.iloc[j]:
            s += 1
    Sk[i] = s
    E = (i+1)*(i/4)
    Var = (i+1)*i*(2*(i+1)+5)/72
    UFk[i] = (Sk[i] - E)/np.sqrt(Var)

# 逆序计算
# 定义逆累计量序列Sk2
# 定义逆统计量序列Sk2
y2 = np.zeros(n)
Sk2 = np.zeros(n)
UBk = np.zeros(n)

s = 0
y2 = y[::-1]

for i in range(1, n):
    for j in range(0,i):
        if y2.iloc[i] > y2.iloc[j]:
            s += 1
    Sk2[i] = s
    E = (i+1)*(i/4)
    Var = (i+1)*i*(2*(i+1)+5)/72
    UBk[i] = -(Sk2[i] - E)/np.sqrt(Var)

UBk2 = UBk[::-1]


# 画图
plt.figure(figsize=(7, 6), dpi=350)
plt.plot(range(18),UFk, label='UF', color='black',marker='s')
plt.plot(range(18), UBk2, label='UB',color='black', linestyle='--', marker='o')
plt.ylabel('Mann-Kendall检验值')
plt.xlabel('年份 Year')

# 添加辅助线
x_lim = plt.xlim()
# 添加显著水平线和y=0
plt.plot(x_lim,[-1.96,-1.96],':',color='black',label='5%显著水平')
plt.plot(x_lim, [0,0],'--',color='black')
plt.plot(x_lim,[1.96,1.96],':',color='black')
plt.xticks(range(18), x.tolist(), rotation=45)
# plt.legend(loc='upper right', bbox_to_anchor=(0.9,0.95),ncol=3,fancybox=True)

# 设置图例位置，第一个参数调整左右位置，第二个参数调整上下位置
plt.legend(bbox_to_anchor=(0.75,0.07), facecolor='w',frameon=False)
# 添加文本注释
plt.text(0,-1.6,'突变点检验')
plt.savefig("../IMG/MK检验.png")
plt.show()

结果

更新code

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt


class Mk:

    def __init__(self, filepath: str, int_x: int, int_y: int):
        """
        :param filepath: 文件路径 文件格式为.xls、.xlsx
        :param da_x: x轴数据列号
        :param da_y: y周数据列号
        """
        self.__filepath = filepath
        self.__da_x = int_x
        self.__da_y = int_y
        self.__da_x_content = None
        self.__da_y_content = None

    @property
    def da_x_content(self):
        return self.__da_x_content

    @property
    def da_y_content(self):
        return self.__da_y_content

    def read_data(self):
        data = pd.read_excel(self.__filepath)
        self.__da_x_content = data.iloc[:, self.__da_x]
        self.__da_y_content = data.iloc[:, self.__da_y]

    @staticmethod
    def __cal_mk_process(y):
        n = len(y)

        # 正序计算
        # 定义累计量序列Sk，长度n，初始值为0
        Sk = np.zeros(n)
        UFk = np.zeros(n)

        # 定义Sk序列元素s
        s = 0

        for i in range(1, n):
            for j in range(0, i):
                if y.iloc[i] > y.iloc[j]:
                    s += 1
            Sk[i] = s
            E = (i + 1) * (i / 4)
            Var = (i + 1) * i * (2 * (i + 1) + 5) / 72
            UFk[i] = (Sk[i] - E) / np.sqrt(Var)

        # 逆序计算
        # 定义逆累计量序列Sk2
        # 定义逆统计量序列Sk2
        y2 = np.zeros(n)
        Sk2 = np.zeros(n)
        UBk = np.zeros(n)

        s = 0
        y2 = y[::-1]

        for i in range(1, n):
            for j in range(0, i):
                if y2.iloc[i] > y2.iloc[j]:
                    s += 1
            Sk2[i] = s
            E = (i + 1) * (i / 4)
            Var = (i + 1) * i * (2 * (i + 1) + 5) / 72
            UBk[i] = -(Sk2[i] - E) / np.sqrt(Var)

        UBk2 = UBk[::-1]
        return UFk, UBk2

    @staticmethod
    def make_img(x, UFk, UBk2, x_label = '年份 Year', y_label = 'Mann-Kendall检验值', lr = 0.75, tb = 0.07,):
        plt.rcParams['font.family'] = ['SimHei']
        plt.rcParams['axes.unicode_minus'] = False
        # 画图
        plt.figure(figsize=(7, 6), dpi=350)
        plt.plot(range(len(x)), UFk, label='UF', color='black', marker='s')
        plt.plot(range(len(x)), UBk2, label='UB', color='black', linestyle='--', marker='o')
        plt.ylabel(y_label)
        plt.xlabel(x_label)

        # 添加辅助线
        x_lim = plt.xlim()
        # 添加显著水平线和y=0
        plt.plot(x_lim, [-1.96, -1.96], ':', color='black', label='5%显著水平')
        plt.plot(x_lim, [0, 0], '--', color='black')
        plt.plot(x_lim, [1.96, 1.96], ':', color='black')
        plt.xticks(range(len(x)), x.tolist(), rotation=45)
        # plt.legend(loc='upper right', bbox_to_anchor=(0.9,0.95),ncol=3,fancybox=True)

        # 设置图例位置，第一个参数调整左右位置，第二个参数调整上下位置
        plt.legend(bbox_to_anchor=(lr, tb), facecolor='w', frameon=False)
        # 添加文本注释
        plt.text(0, -1.6, '突变点检验')
        plt.show()

    def cal_mk(self):
        return self.__cal_mk_process(self.da_y_content)


if __name__ == '__main__':
    mk = Mk('data.xls', 0, 1) # 列数据
    mk.read_data()
    UFk, UBk2 = mk.cal_mk()
    mk.make_img(mk.da_x_content, UFk, UBk2) # 可通过x_label, y_label控制x，y轴标签
    # mk.make_img(mk.da_x_content, UFk, UBk2, "x", "y")
    # mk.make_img(mk.da_x_content, UFk, UBk2, "x", "y", 0.9, 0.9)# 通过lr，tb控制图例位置

数据

数据链接