近红外光谱建模之区间偏最小二乘法python实现(ipls算法)
目录
1 区间偏最小二乘法原理(ipls)
2 ipls的python实现
3 实验结果图
1 区间偏最小二乘法原理(ipls)
区间偏最小二乘法可以用来提取特征波段,它将整个光谱区域划分为多个等宽的子区间, 假设为n个; 在每个子区间上进行偏最小二乘回归,建立待测品质的"局部回归模型",也就是可以得到n个局部回归模型;以均方根无误差MSE值为各模型的精度衡量标准,取精度最高的局部模型所在的子区间为特征波段。
2 ipls的python实现
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from utility_spectrum import spxy, ipls
import scipy.io as sio
from sklearn.cross_decomposition import PLSRegression
from sklearn.metrics import mean_squared_error
def splitspectrum(interval_num, x_train, x_test):
"""
:param interval_num: int (common values are 10, 20, 30 or 40)
:param x_train: shape (n_samples, n_features)
:param x_test: shape (n_samples, n_features)
:return: x_train_block:intervals splitting for training sets(dict)
x_test_black: intervals splitting for test sets (dict)
"""
feature_num = x_train.shape[1]
x_train_block = {}
x_test_black = {}
remaining = feature_num % interval_num # 用于检查是否能等分
# (一)特征数量能够等分的情况
if not remaining:
interval_size = feature_num / interval_num # 子区间波点数量
for i in range(1, interval_num+1):
# (1)取对应子区间的光谱数据
feature_start, feature_end = int((i-1) * interval_size), int(i * interval_size)
x_train_block[str(i)] = x_train[:, feature_start:feature_end]
x_test_black[str(i)] = x_test[:, feature_start:feature_end]
# (二)特征数量不能等分的情况(将多余波点等分到后面的几个区间里)
else:
separation = interval_num - remaining # 前几个区间
intervalsize1 = feature_num // interval_num
intervalsize2 = feature_num // interval_num + 1
# (2)前几个子区间(以separation为界)
for i in range(1, separation+1):
feature_start, feature_end = int((i-1) * intervalsize1), int(i * intervalsize1)
x_train_block[str(i)] = x_train[:, feature_start:feature_end]
x_test_black[str(i)] = x_test[:, feature_start:feature_end]
# (3)后几个子区间(以separation为界)
for i in range(separation+1, interval_num+1):
feature_s = int((i - separation-1) * intervalsize2) + feature_end
feature_e = int((i - separation) * intervalsize2) + feature_end
x_train_block[str(i)] = x_train[:, feature_s:feature_e]
x_test_black[str(i)] = x_test[:, feature_s:feature_e]
return x_train_block, x_test_black
def ipls(intervals, x_train, x_test, y_train, y_test):
"""
:param intervals: 区间数量
:param x_train: shape (n_samples, n_features)
:param x_test: shape (n_samples, n_features)
:param y_train: shape (n_samples, )
:param y_test: shape (n_samples, )
:return:
"""
x_train_block, x_test_black = splitspectrum(intervals, x_train, x_test)
mse = []
for i in range(1, intervals + 1):
print("当前区间:", i)
x_train_interval, x_test_interval = x_train_block[str(i)], x_test_black[str(i)]
current_fn = x_train_interval.shape[1]
if current_fn >= 100:
ncom_upper = 100
elif current_fn >= 50:
ncom_upper = current_fn - 10
else:
ncom_upper = current_fn - 5
ncomp = np.arange(5, ncom_upper)
error = []
for nc in ncomp:
print("迭代当前主成分数量:", nc)
pls = PLSRegression(n_components=nc,
scale=True,
max_iter=500,
tol=1e-06,
copy=True)
pls.fit(x_train_interval, y_train.reshape(-1, 1))
y_test_pred = pls.predict(x_test_interval)
mse_temp = mean_squared_error(y_test, y_test_pred.ravel())
error.append(mse_temp)
mse.append(np.min(error))
print(mse)
plt.figure(figsize=(5.5, 4), dpi=300)
plt.bar(np.arange(1, intervals + 1), mse, width=0.5, color='bgrk', linewidth=0.4)
plt.xlabel("intervals")
plt.ylabel("mse")
plt.show()
# 1.数据获取
mat = sio.loadmat('ndfndf.mat')
data = mat['ndfndf']
x, y = data[:, :1050], data[:, 1050]
print(x.shape, y.shape)
# 2.样本集划分
x_train, x_test, y_train, y_test = spxy(x, y, test_size=0.33)
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
intervals = 20
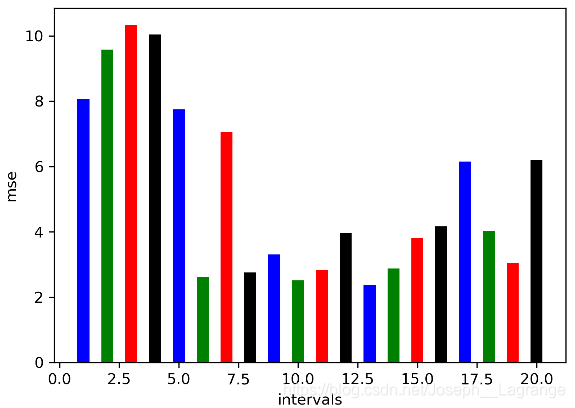
ipls(intervals, x_train, x_test, y_train, y_test)3 实验结果图
划分为20 个区间