python偏最小二乘法回归分析_Python 实现最小二乘法拟合直线

线性回归

线性回归是回归分析中最常见的一种建模方式。当因变量是连续的，自变量是连续的或者离散的，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。

用方程 y = mx + c，其中 y为结果，x为特征，m为系数，c为误差 在数学中m为梯度c为截距。

最小二乘法

最小二乘法用于求目标函数的最优值，它通过最小化误差的平方和寻找匹配项所以又称为：最小平方法；这里将用最小二乘法用于求得线性回归的最优解

关于最小二乘法推导过程，详见这篇博客 最小二乘法

pandas 处理数据

导入 pandas 模块

import pandas as pd

import matplotlib.pyplot as plt

# jupyter 关于绘图的参数配置

plt.style.use('ggplot')

%config InlineBackend.figure_format = 'retina'

%matplotlib inline

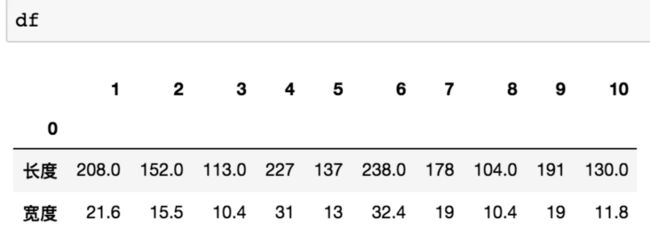
获取表示长度和宽度关系的几组数据

数据不是很完美，接下来利用 pandas 处理下

修改列名

重置索引

df = df.rename(columns={'Unnamed: 0':'0'})

df = df.set_index(keys=['0'])

为了分析长度和宽度之间的线性关系，分别获取长度和宽度的一维数据

xcord = df.loc['长度']

ycord = df.loc['宽度']

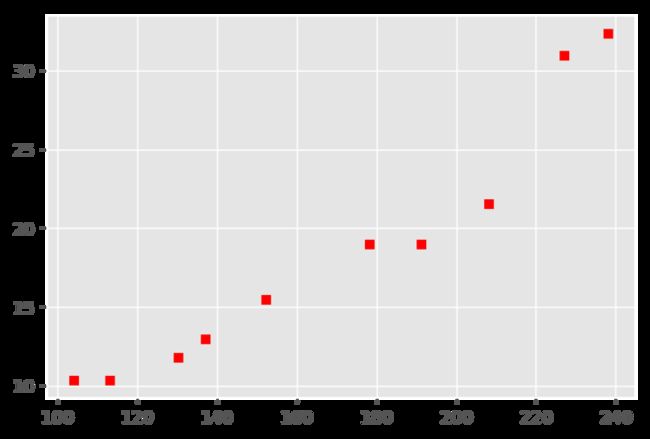
plt.scatter(xcord,ycord,s=30,c='red',marker='s')

从宽度和长度的数据分布，可以看出具有一定的线性关系，接下来我们用最小二乘法来拟合这条直线

最小二乘法的计算过程

## xy 的均值

(xcord*ycord).mean()

## x 的均值乘以 y 的均值

xcord.mean()* ycord.mean()

## x 的平方均值

pow(xcord,2).mean()

## x 的均值的平方

pow(xcord.mean(),2)

# m 分子是 xy 的均值减去 x 的均值乘以 y 的均值；

# m 分母是 x 平方的均值 减去 x 的均值的平方

m = ((xcord*ycord).mean() - xcord.mean()* ycord.mean())/(pow(xcord,2).mean()-pow(xcord.mean(),2))

# c 等于 y 的均值 - m 乘以 x 的均值

c = ycord.mean() - m*xcord.mean()

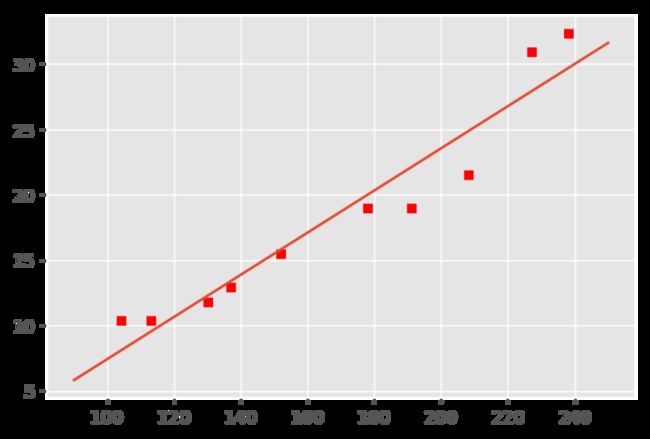
# 绘图

plt.scatter(xcord,ycord,s=30,c='red',marker='s')

x=np.arange(90.0,250.0,0.1)

y=m*x+c

plt.plot(x,y)

plt.show()

Python 建模

处理数据，计算相关系数矩阵，提取特征和标签

df = pd.read_csv('./zuixiaoerchengfa.csv',encoding='gbk')

df.rename(columns={"Unnamed: 0":""},inplace=True)

df.set_index(keys="",inplace=True)

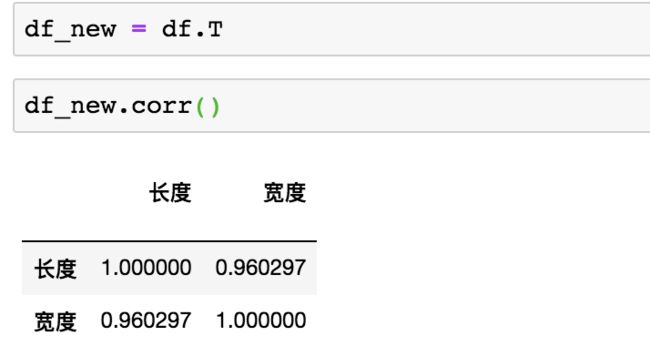
df_new = df.T

df_new.corr()

xcord = df_new['长度']

ycord = df_new['宽度']

引入 sklearn 模块得到训练集和测试集

from sklearn.model_selection import train_test_split

import matplotlib.pyplot as plt

plt.style.use('ggplot')

%config InlineBackend.figure_format = 'retina'

%matplotlib inline

# 训练数据、测试数据遵循二八法则

x_train,x_test,y_train,y_test = train_test_split(xcord, ycord, train_size = 0.8, test_size = 0.2)

# 从图可以看出两个特征之间适合简单线性回归模型

plt.scatter(x_train,y_train,c = 'g')

plt.xlabel("L")

plt.ylabel("H")

创建线性回归模型

from sklearn.linear_model import LinearRegression

model = LinearRegression()

# model.fit model.score 需要传递二维列表，故通过 reshape 重塑

x_train = x_train.values.reshape(-1,1)

y_train = y_train.values.reshape(-1,1)

model.fit(x_train,y_train)

# 计算出拟合的最小二乘法方程

# y = mx + c

c = model.intercept_

m = model.coef_

c = round(float(c),2)

m = round(float(m),2)

print("最小二乘法方程 : y = {} + {}x".format(c,m))

评估模型

x_test = x_test.values.reshape(-1,1)

y_test = y_test.values.reshape(-1,1)

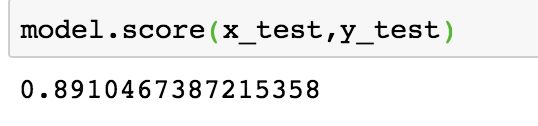
model.score(x_test,y_test)

可视化效果

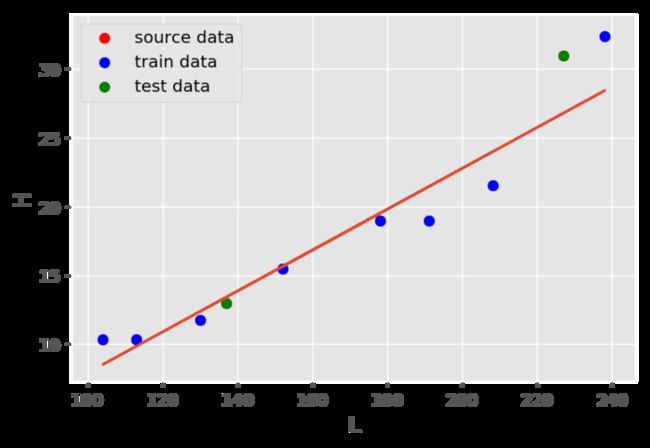
通过可视化效果来感受模型拟合效果

x_train_result = model.predict(x_train)

plt.scatter(xcord,ycord,c = 'r', label = "source data")

plt.scatter(x_train,y_train, c = 'b',label = "train data")

plt.scatter(x_test,y_test,c = 'g',label = "test data")

plt.xlabel("L")

plt.ylabel("H")

plt.legend(loc="upper left")

plt.plot(x_train,x_train_result)