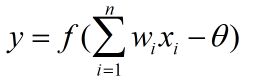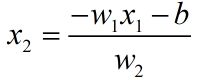在说起感知器之前,需要先说一下神经网络的定义:
神经网络是由具有适应性的简单单元组成的广泛并行互联的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
感知器(M-P神经元模型)
感知器(Perceptron)由两层神经元组成,如图所示,输入层接收外界输入信号后传递给输出层,输出层是M-P神经元,亦称“阈值逻辑单元”。在M-P神经元模型中,神经元接收到来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过“激活函数”(activation function)处理以产生神经元的输出。
理想中的激活函数是下图所示的阶跃函数,它将输入值映射为输出值“0”或“1”,显然“1”对应于神经元兴奋,“0”对应于神经元抑制。然而,阶跃函数具有不连续、不光滑等不太好的性质,因此实际常用Sigmoid函数作为激活函数,如图所示,它把可能在较大范围内变化的输入值挤压到(0,1)输出范围内,因此,有时也称为“挤压函数”。
把许多个这样的神经元按一定的层次结构连接起来,就得到了神经网络。
感知器能很容易地实现逻辑与、或、非的运算,注意到
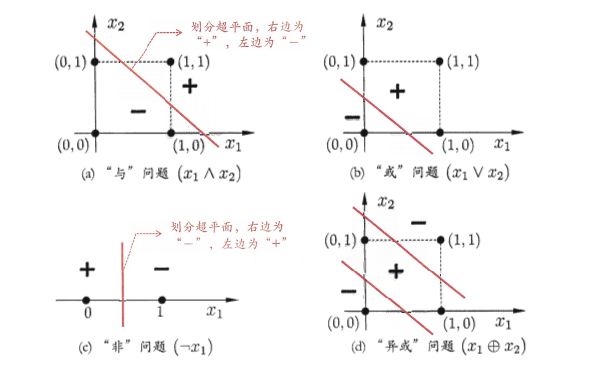
假定函数f为图(a)中的阶跃函数,且x1,x2的取值为0或1,下面通过有两个输入神经元的感知器来实现逻辑与、或、非的运算。
- “与”(x1∧x2):令w1=w2=1,θ=2,则
仅在x1=x2=1时,y=1;
- “或”(x1∨x2):令w1=w2=1,θ=0.5,则
当x1=1或x2=1时,y=1;
- “非”(¬x1):令w1=-0.6,w2=0,θ=-0.5,则
当x1=1时,y=0;当x1=0时,y=1;
更一般地,给定训练数据集,权重wi(i=1,2,.... , n)以及阈值θ可通过学习得到,阈值θ可看作一个固定输入为-1.0的哑结点所对应的连接权重w(n+1),这样,权重和阈值的学习就可统一为权重的学习。
感知器权重(w)更新策略
感知器学习规则非常简单,对训练样例(x,y),若当前感知器的输出为![]() ,则感知器权重将这样调整:
,则感知器权重将这样调整:
其中η∈(0, 1)称为学习率(learning rate),从上式可看出,若感知器对训练样例(x,y)预测正确,即![]() ,则感知器不发生变化,否则将根据错误的程度进行权重调整。
,则感知器不发生变化,否则将根据错误的程度进行权重调整。
单层感知器的缺陷
需要注意的是,单层感知器只有输出层神经元进行激活函数处理,即只拥有一层功能神经元(functional neuron),其学习能力非常有限,事实上,上述与、或、非问题都是线性可分的问题,可以证明,若两类模式是线性可分的,即存在一个线性超平面能将它们分开,感知器的学习过程一定会收敛(converge)而求得适当的权向量w=(w1;w2;.... ;wn;w(n+1));否则感知器学习过程将会发生振荡,w难以稳定下来,不能求得合适的解。即使是非常简单的非线性可分问题也不能解决,如:异或问题。
多层网络
要解决非线性可分问题,需要考虑使用多层功能神经元。例如图5.5中这个简单的两层感知器就能解决异或问题,在图中,输出层与输入层之间的一层神经元,被称为隐层或隐含层(hidden layer),隐含层和输入层神经元都是拥有激活函数的功能神经元。
更一般地,常见的神经网络是形如图5.6所示的层级结构,每层神经元与下一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接,这样的神经网络结构通常称为“多层前馈神经网络”,其中输入层神经元接收外界输入,隐层与输入层神经元对信号进行加工,最终结果由输出层神经元输出;换言之,输入层神经元仅是接受输入,不进行函数处理,隐层与输出层包含功能神经元。因此,图5.6(a)通常被称为“两层网络”,即称为单隐层网络,只需包含隐层,即可称为多层网络。神经网络的学习过程,就是根据训练数据来调整神经元之间的“连接权”以及每个功能神经元的阈值;换言之,神经网络“学”到的东西,蕴含在连接权与阈值中。
利用感知器实现线性分类
接下来通过单层感知器来实现对样本的线性分类,这里选用的激活函数为符号函数:
为了处理方便,这里将x=0的情况归为sgn(0)=1,即
# 导入一些需要的包
import random
import numpy as np
import matplotlib.pyplot as plt# 定义自定义的符号函数
def sign(vec):
if vec >= 0:
return 1
else:
return -1# 训练权重和阈值
def train(train_num, train_datas, lr): # lr为学习率
w = [0, 0]
b = 0
for i in range(train_num):
x = random.choice(train_datas) # 从序列中获取一个随机元素
x1, x2, y = x # 把随机选取的样本的分量依次赋值给x1,x2,y
if(y*sign((w[0]*x1 + w[1]*x2 + b)) <= 0): # 训练算法,如果符号函数与输出结果不一致,则更新权重和阈值
w[0] += lr*y*x1
w[1] += lr*y*x2
b += lr*y
return w, b # 最终返回训练完成的权重和阈值# 通过画图来查看模型对样本分类的好坏
def plot_points(train_datas, w, b):
plt.figure() # 创建图表
x1 = np.linspace(0, 8, 100)
x2 = (-b-w[0]*x1)/w[1] # 分类直线满足的方程
plt.plot(x1, x2, color='r', label='y1 data') # 画出分类直线
datas_len = len(train_datas) # 看有几行,几个样本
for i in range(datas_len):
if(train_datas[i][-1]==1): # 正样本用圆点标记,向量的最后一个分量[-1],也可以用[2]
plt.scatter(train_datas[i][0], train_datas[i][1], s=50)
else:
plt.scatter(train_datas[i][0], train_datas[i][1], marker='x',s=50) # 负样本用x标记
plt.show() # 画图在上段程序中,对于已经训练好的权重和阈值,满足:
所以有
# 执行程序
if __name__=='__main__':
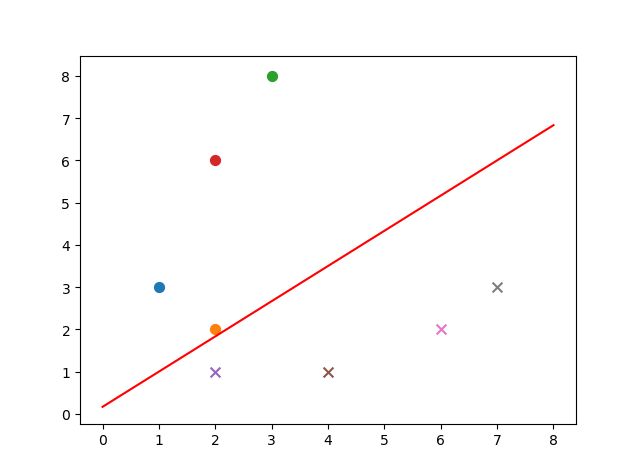
train_data1 = [[1, 3, 1], [2, 2, 1], [3, 8, 1], [2, 6, 1]] # 正样本
train_data2 = [[2, 1, -1], [4, 1, -1], [6, 2, -1], [7, 3, -1]] # 负样本
train_datas = train_data1 + train_data2 # 样本集
print(train_datas)
w, b = train(train_num=50, train_datas=train_datas, lr=0.01) # 训练50次
plot_points(train_datas, w, b) # 画出样本点及分类直线显示结果:
在以后的博客中,逐渐涉及多层神经网络的构建与应用,深入其中,更能体会到神经网络的奥妙。
参考:
1、机器学习/周志华著.--北京:清华大学出版社,2016(2017.3重印)