python3 4.单层感知器与线性神经网络的应用 学习笔记

前言

     计算机视觉系列之学习笔记主要是本人进行学习人工智能（计算机视觉方向）的代码整理。本系列所有代码是用python3编写，在平台Anaconda中运行实现，在使用代码时，默认你已经安装相关的python库，这方面不做多余的说明。本系列所涉及的所有代码和资料可在我的github或者码云上下载到，gitbub地址：https://github.com/mcyJacky/DeepLearning-CV，如有问题，欢迎指出~。

一、单层感知器简介

1.1 什么是单层感知器

     在学习机器学习中的神经网络时，单层感知器应该是最简单的神经网络。下面通过如下单层感知器结构图进行描述：

图1.1 单层感知器结构表示1

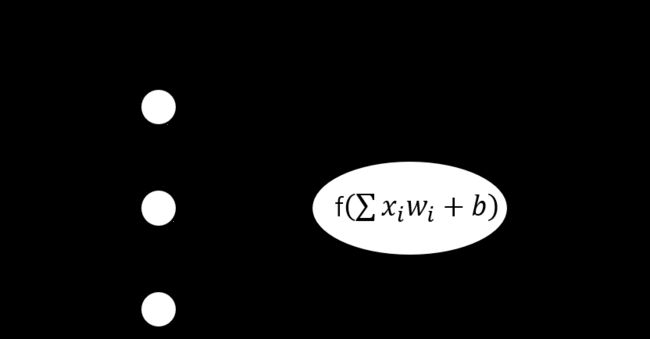
     如图1.1所示，单层感知器神经网络由输入层和输出层组成，其中输入层与输出层通过权值$w_i$进行关联，输入层为训练样本为特征值(图中用$x_1,x_2,x_3$表示)，输出层为预测值$y$。其余参数：$b$为偏置值，函数$f(z)$为对应的激活函数。即由公式$$y=f(\sum (x_i{w}_i)+b)$$可知，预测值与权值和偏置值有关。在实际使用过程中就是通过不断调整权值和偏置值来修正预测值与正确标签的误差。

     为了书写方便，我们将偏置项$b$不单独写出，而是在神经网络输入层添加一个固定的特征$x_0=1$，所对应的权值为$w_0$，如下图1.2所示：

图1.2 单层感知器结构表示2

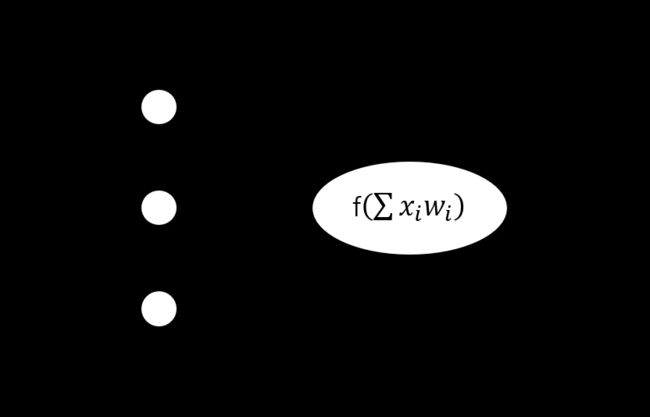
1.2 单层感知器相应的计算规则

     下面会直接给出推导结果，具体推导过程请自行参考相关书籍或资料。由公式$$y=f(\sum (x_i{w}_i))$$
     根据反向传播的推导可知，权值的梯度变化值为：$$\Delta w_i=\eta (t-y)x_i$$
其中，$\eta$为学习率，$t$为实际正确值标签，$y$为预测值标签，$x_i$为个特征值。
     由梯度下降法得：
$$w_i:=w_i+\Delta w_i$$

二、单层感知器应用

      我们定义二维特征输入数据，输出标签为1或-1。定义训练数据集有4个，如下代码：

import numpy as np
import matplotlib.pyplot as plt

#定义输入数据
X = np.array([[1,3,3],
              [1,4,3],
              [1,1,1],
              [1,2,1]])

#定义标签, 即[3,3] -> 1, [4,3] -> 1
T = np.array([[1],
             [1],
             [-1],
             [-1]])

#权值初始化,3行1列权值矩阵
W = np.random.random([3,1])

#学习率
lr = 0.1

#进行训练，更新权值
def train():
    global X,T,W,lr
    #预测值(4,1)
    Y = np.sign(np.dot(X,W))
    #误差:实际标签值与预测值的误差(4,1)
    E = T-Y
    delta_W = lr*(X.T.dot(E)) / X.shape[0]
    W = W + delta_W

#训练模型
for i in range(100):
    #更新权值
    train()
    #打印当前训练次数
    print('epoch: ', i + 1)
    #当前权值
    print('weight: ', W)
    #当前预测值
    Y = np.sign(np.dot(X,W))
    #all()表示Y中所有值和T中的所有值都对应相等,才为真
    if (Y == T).all():
        print("Finished")
        break

#部分输出结果：
#epoch:  1
# weight:  [[0.73214673]
#  [0.26753341]
#  [0.23937169]]
# epoch:  2
# weight:  [[0.63214673]
#  [0.11753341]
#  [0.13937169]]
# ...
# ...
# epoch:  17
# weight:  [[-0.06785327]
#  [ 0.01753341]
#  [ 0.33937169]]
# epoch:  18
# weight:  [[-0.16785327]
#  [-0.13246659]
#  [ 0.23937169]]
# Finished

      我们对输入特征和预测结果进行可视化显示：

#正样本的xy坐标
x1 = [3,4]
y1 = [3,3]
#负样本
x2 = [1,2]
y2 = [1,1]

#定义分界线的斜率和截距
#计算方法： y = w0 + w1*x1 + w2*x2 => y>0,预测值为1，当y<0时，预测值为-1。所以直线可用
#			w0 + w1*x1 + w2*x2 = 0表示，令 x=x1,y=x2 => y = (-W[1]/W[2]) * x + (-W[0]/W[2])
k = -W[1]/W[2] #斜率
d = -W[0]/W[2] #截距
#设定两个点
xdata = (0,3)
plt.plot(xdata, xdata*k + d, 'r')

#正样本的点
plt.scatter(x1,y1,c='b')
#负样本的点
plt.scatter(x2,y2,c='y')
plt.show()

可视化结果显示如下：

图2.1 预测结果可视化

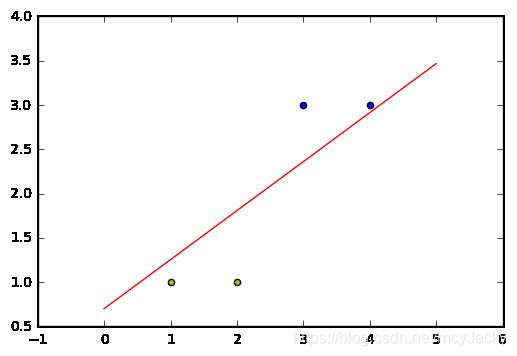
      由图2.1所示，经过训练迭代，可以计算出相应的$w_i$的权值来进行输入特征值的分类。

三、线性神经网络应用

      还是使用单层感知器的例子，只要对训练函数进行稍加修改，就能运用线性神经网络。修改训练函数如下：

# 更新权值函数
def train():
    global X,Y,W,lr,T
    # 同时计算4个数据的预测值，Y(4，1)
    Y = np.dot(X,W) #修改点：线性神经网络输出值不一定是1或-1,所以不需要使用符号函数，
    # T-Y得到4个标签值与预测值的误差E(4，1)
    E = T - Y
    # 计算权值的变化
    delta_W = lr * (X.T.dot(E)) / X.shape[0]
    # 更新权值
    W = W +delta_W

# 我们也可以通过每步的迭代，来可视化观察线性拟合的结果
# 训练模型
for i in range(100):
    # 更新权值
    train()
    
    # 画图
    # 正样本的xy坐标
    x1 = [3,4]
    y1 = [3,3]
    # 负样本xy坐标
    x2 = [1,2]
    y2 = [1,1]
    # 定义分类边界线的斜率和截距
    k = -W[1]/W[2]
    d = -W[0]/W[2]
    # 设定两个点
    xdata = (0, 5)
    # 通过两点来确定一条直线，用红色的线来画出分界线
    plt.plot(xdata,xdata*k+d,'r')
    # 用蓝色的点画正样本
    plt.scatter(x1,y1,c='b')
    # 用黄色的点画负样本
    plt.scatter(x2,y2,c='y')
    plt.show()

部分线性拟合的过程：

图2.2 部分线性拟合过程

四、小结

      本篇我们用最简单的案例，来描述单层感知器和线性神经网络，所用的输入数据特征是可以被线性分类的。如果输入数据类似于异或问题，数据是不能被线性分类的情况，线性神经网络就不能拟合成功，我们就需要其他的神经网络结构设计，如BP神经网络等。

【参考】：
     1. 城市数据团课程《AI工程师》计算机视觉方向
     2. deeplearning.ai 吴恩达《深度学习工程师》
     3. 《机器学习》作者：周志华

---

转载声明：
版权声明：非商用自由转载-保持署名-注明出处
署名 ：mcyJacky
文章出处：https://blog.csdn.net/mcyJacky