深度学习实验二 pytorch入门
一. 概念:张量、算子
张量的定义是矩阵的扩展与延伸,我认为张量就是n个数量的n维数组,也可认为是高阶的矩阵。算子的定义是构建复杂机器学习模型的基础组件,我觉得算子是一个算法单元,就是一个可以进行某种操作的函数。
二. 使用pytorch实现张量运算
1.2 张量
1.2.1 创建张量
1.2.1.1 指定数据创建张量
a=torch.tensor([2.0,3.0,4.0]) #创建一个一维张量
b=torch.tensor([[1.0,2.0,3.0],[4.0,5.0,6.0]]) #创建一个二维张量
c=torch.tensor([[[1,2,3,4,5],
[6,7,8,9,10]],
[[11,12,13,14,15],
[16,17,18,19,20]]]) #创建一个三维张量
print(a);print(b);print(c)运行结果:
1.2.1.2 指定形状创建
a=torch.zeros(2,3) #创建数据全为1,形状为[2,3]的张量
b=torch.ones(2,3) ##创建数据全为0,形状为[2,3]的张量
c=torch.full([2,3],10) ##创建数据全为指定值,形状为[2,3]的张量
print(a);print(b);print(c)运行结果:
1.2.1.3 指定区间创建
a=torch.linspace(0,666,6)
print(a)运行结果:
1.2.2 张量的属性
1.2.2.1 张量的形状
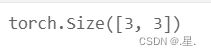
a=torch.Tensor([[1,1,1],[2,2,2],[3,3,3]])
print(a.shape)运行结果:
1.2.2.2 形状的改变
a=torch.Tensor([[1,1,1],[2,2,2],[3,3,3]])
print(a.reshape(9,1))运行结果:
1.2.2.3 张量的数据类型
a=torch.Tensor([[1,1,1],[2,2,2],[3,3,3]])
a.type()运行结果:
1.2.2.4 张量的设备位置
a=torch.Tensor([[1,1,1],[2,2,2],[3,3,3]])
print(a.device)运行结果:
1.2.3 张量与Numpy数组转换
numpy转换成张量
a=np.array([[1,1,1],[2,2,2],[3,3,3]])
b=torch.Tensor(a)
print(b)运行结果:
张量转化为numpy
a=torch.Tensor([[1,1,1],[2,2,2],[3,3,3]])
b=a.numpy()
print(b)运行结果:
1.2.4 张量的访问
1.2.4.1 索引和切片
张量的索引与切片
a=torch.Tensor([[1,1,1],[2,2,2],[3,3,3]])
print(a[-1]) #索引
print(a[1:3]) #切片运行结果:
1.2.4.2 访问张量
a=torch.Tensor([[1,1,1],[2,2,2],[3,3,3]])
print(a[1,2]) #访问第一行第二列
print(a[[1,0],[1,1]]) #访问第一行第一列与第零行第一列运行结果:
1.2.4.3 修改张量
a=torch.Tensor([[1,1,1],[2,2,2],[3,3,3]])
a[0,1]=2
a[1]=-2
print(a)运行结果:
1.2.5 张量的运算
1.2.5.1 数学运算
a=torch.Tensor([[1,1,1],[2,2,2],[3,3,3]])
print(a)
a+=1
print(a) #加法
a-=2
print(a) #减法
a*=2
print(a) #乘法
a/=2
print(a) #除法
a = torch.sqrt(a)
print(a) #求平方根运行结果:
1.2.5.2 逻辑运算
a=torch.Tensor([1,0,2,0]).bool()
b=torch.Tensor([0,3,1,0]).bool()
print(torch.isfinite(a)) #判断张量中元素是否是有限的数字
print(torch.equal(a,b)) #判断两个张量的全部元素是否相等
print(torch.eq(a,b)) #判断两个张量的每个元素是否相等
print(torch.all(a)) #判断是否全为True运行结果:
1.2.5.3 矩阵运算
x=torch.Tensor([2,2,2])
y=torch.Tensor([3,3,3])
z=torch.Tensor([[2,2,2],[3,3,3]])
print(torch.dot(x,y)) #点积
print(torch.mv(z,x)) #向量积
a=torch.Tensor([[1,1,1],[2,2,2],[3,3,3]])
b=torch.Tensor([[6,6,6],[5,5,5],[4,4,4]])
print(torch.mm(a,b)) #矩阵乘法运行结果:
1.2.5.4 广播机制
广播机制允许在一些运算时使用不同形状的张量。通常来讲,如果有一个形状较小和一个形状较大的张量,会希望多次使用较小的张量来对较大的张量执行某些操作,看起来像是形状较小的张量首先被扩展到和较大的张量形状一致,然后再做运算。
广播机制的条件
1)每个张量至少为一维张量。
2)从后往前比较张量的形状,当前维度的大小要么相等,要么其中一个等于1,要么其中一个不存在。
a=torch.Tensor([1,1,1])
b=torch.Tensor([[1,1,1],[2,2,2],[3,3,3]])
print(a.shape)
print(b.shape)
print(a+b) #广播发生运行结果:
三. 使用pytorch实现数据预处理
1. 读取数据集 house_tiny.csv、boston_house_prices.csv、Iris.csv
引入pandas库读取数据集
data_house_tiny = pd.read_csv('house_tiny.csv')
data_boston_house_prices = pd.read_csv('boston_house_prices.csv')
data_iris = pd.read_csv('Iris.csv')
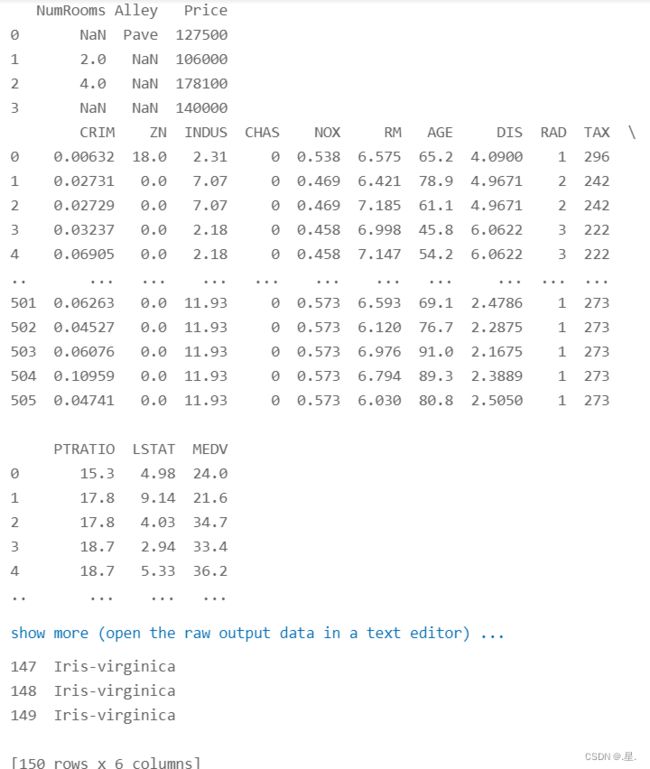
print(data_house_tiny)
print(data_boston_house_prices)
print(data_iris)运行结果:
2. 处理缺失值
以数据集 house_tiny.csv为例
data_house_tiny = pd.read_csv('house_tiny.csv')
data_boston_house_prices = pd.read_csv('boston_house_prices.csv')
data_iris = pd.read_csv('Iris.csv')
fillna_house_tiny=data_house_tiny.fillna(0) #用0填充NaN
dropna_house_tiny=data_house_tiny.dropna() #删除缺失值
print(fillna_house_tiny)
print(dropna_house_tiny)运行结果:
3. 转换为张量格式
data_house_tiny = pd.read_csv('house_tiny.csv')
fillna_house_tiny=data_house_tiny.fillna(0) #用0填充NaN
torch_house_tiny=torch.Tensor=(fillna_house_tiny.values) #读出数据并转换为张量
print(torch_house_tiny)运行结果:
心得体会: 此次实验,我们了解到了张量的各种概念与使用方法,如创建、转化、计算等等,同时也进行了数据集的读取、处理缺失值、转换为张量格式的操作,对数据的处理有了初步认识。