NNDL 实验六 卷积神经网络（1）卷积
NNDL 实验六 卷积神经网络（1）卷积
- 5.1 卷积
-
- 5.1.1 二维卷积运算
- 5.1.2 二维卷积算子
- 5.1.3 二维卷积的参数量和计算量
- 5.1.4 感受野
- 5.1.5 卷积的变种
-
- 5.1.5.1 步长（Stride）
- 5.1.5.2 零填充（Zero Padding）
- 5.1.6 带步长和零填充的二维卷积算子
- 5.1.7 使用卷积运算完成图像边缘检测任务
- 选做题
-
- 1.实现一些传统边缘检测算子，如：Roberts、Prewitt、Sobel、Scharr、Kirsch、Robinson、Laplacian。
- 2.实现的简易的 Canny 边缘检测算法。
- 3.复现论文 Holistically-Nested Edge Detection，发表于 CVPR 2015
- 4.复现论文 Richer Convolutional Features for Edge Detection，CVPR 2017 发表
- 5.【CED】添加了反向细化路径的 HED 模型 - 飞桨AI Studio (baidu.com)
- 总结:
- 参考
5.1 卷积
卷积神经网络（Convolutional Neural Network，CNN）
- 受生物学上感受野机制的启发而提出。
- 一般是由卷积层、汇聚层和全连接层交叉堆叠而成的前馈神经网络
- 有三个结构上的特性：局部连接、权重共享、汇聚。
- 具有一定程度上的平移、缩放和旋转不变性。
- 和前馈神经网络相比，卷积神经网络的参数更少。
- 主要应用在图像和视频分析的任务上，其准确率一般也远远超出了其他的神经网络模型。
- 近年来卷积神经网络也广泛地应用到自然语言处理、推荐系统等领域。
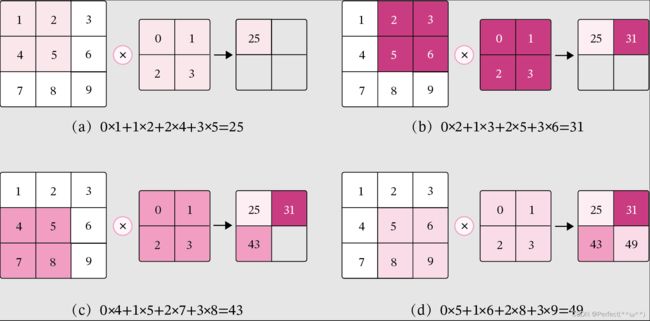
5.1.1 二维卷积运算
5.1.2 二维卷积算子
在本书后面的实现中，算子都继承paddle.nn.Layer，并使用支持反向传播的飞桨API进行实现，这样我们就可以不用手工写backword()的代码实现。
【使用pytorch实现】
import torch
import torch.nn as nn
import torch.nn
import numpy as np
class Conv2D(nn.Module):
def __init__(self, kernel_size):
super(Conv2D, self).__init__()
w = torch.tensor(np.array([[0., 1.], [2., 3.]], dtype='float32').reshape([kernel_size, kernel_size]))
self.weight = torch.nn.Parameter(w, requires_grad=True)
def forward(self, X):
u, v = self.weight.shape
output = torch.zeros([X.shape[0], X.shape[1] - u + 1, X.shape[2] - v + 1])
for i in range(output.shape[1]):
for j in range(output.shape[2]):
output[:, i, j] = torch.sum(X[:, i:i + u, j:j + v] * self.weight, axis=[1, 2])
return output
# 随机构造一个二维输入矩阵
inputs = torch.as_tensor([[[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]])
conv2d = Conv2D(kernel_size=2)
outputs = conv2d(inputs)
print("input: {}, \noutput: {}".format(inputs, outputs))
5.1.3 二维卷积的参数量和计算量
随着隐藏层神经元数量的变多以及层数的加深，
使用全连接前馈网络处理图像数据时，参数量会急剧增加。
如果使用卷积进行图像处理，相较于全连接前馈网络，参数量少了非常多。
5.1.4 感受野
输出特征图上每个点的数值，是由输入图片上大小为U×V的区域的元素与卷积核每个元素相乘再相加得到的，所以输入图像上U×V区域内每个元素数值的改变，都会影响输出点的像素值。我们将这个区域叫做输出特征图上对应点的感受野。感受野内每个元素数值的变动，都会影响输出点的数值变化。比如3×3卷积对应的感受野大小就是3×3，如图。
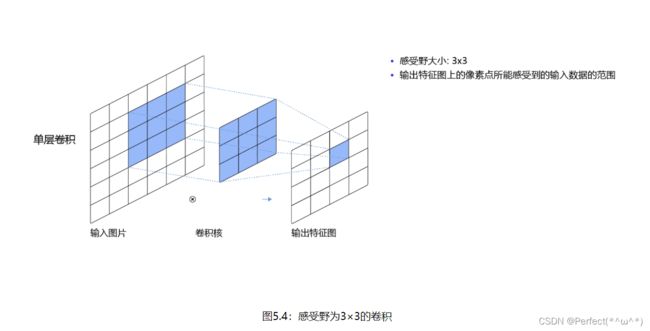
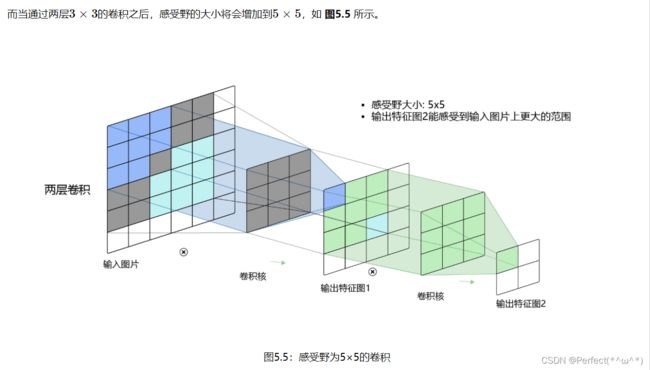因此，当增加卷积网络深度的同时，感受野将会增大，输出特征图中的一个像素点将会包含更多的图像语义信息。
5.1.5 卷积的变种
在卷积的标准定义基础上，还可以引入卷积核的滑动步长和零填充来增加卷积的多样性，从而更灵活地进行特征抽取。
5.1.5.1 步长（Stride）
在卷积运算的过程中，有时会希望跳过一些位置来降低计算的开销，也可以把这一过程看作是对标准卷积运算输出的下采样。
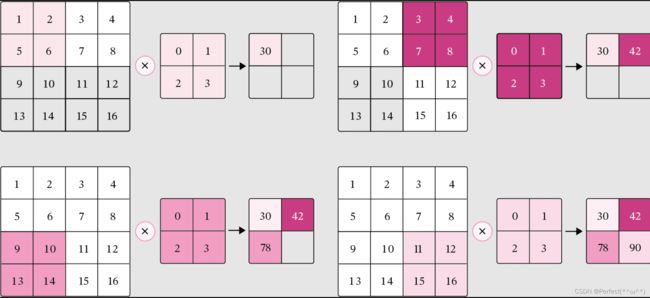
在计算卷积时，可以在所有维度上每间隔S个元素计算一次，S称为卷积运算的步长（Stride），也就是卷积核在滑动时的间隔。
此时，对于一个输入矩阵X∈RM×N和一个滤波器W∈RU×V，它们的卷积为
在二维卷积运算中，当步长S=2时，计算过程如图所示。
5.1.5.2 零填充（Zero Padding）
在卷积运算中，还可以对输入用零进行填充使得其尺寸变大。根据卷积的定义，如果不进行填充，当卷积核尺寸大于1时，输出特征会缩减。对输入进行零填充则可以对卷积核的宽度和输出的大小进行独立的控制。
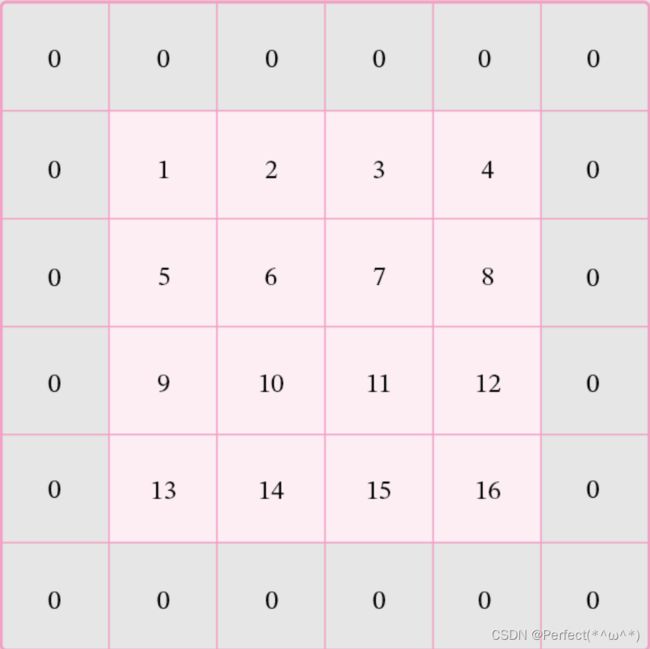
在二维卷积运算中，零填充（Zero Padding）是指在输入矩阵周围对称地补上P个0。图5.7 为使用零填充的示例。
padding=1的零填充：
5.1.6 带步长和零填充的二维卷积算子
引入步长和零填充后，二维卷积算子代码实现如下：
【使用pytorch实现】
import torch
import torch.nn as nn
import torch.nn
import numpy as np
class Conv2D(nn.Module):
def __init__(self, kernel_size,stride=1, padding=0):
super(Conv2D, self).__init__()
w = torch.tensor(np.array([[0., 1., 2.], [3., 4. ,5.],[6.,7.,8.]], dtype='float32').reshape([kernel_size, kernel_size]))
self.weight = torch.nn.Parameter(w, requires_grad=True)
self.stride = stride
self.padding = padding
def forward(self, X):
# 零填充
new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding])
new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X
u, v = self.weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(
new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * self.weight,
axis=[1, 2])
return output
inputs = torch.randn(size=[2, 8, 8])
conv2d_padding = Conv2D(kernel_size=3, padding=1)
outputs = conv2d_padding(inputs)
print("When kernel_size=3, padding=1 stride=1, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))
conv2d_stride = Conv2D(kernel_size=3, stride=2, padding=1)
outputs = conv2d_stride(inputs)
print("When kernel_size=3, padding=1 stride=2, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))
从输出结果看出，使用3×3大小卷积，padding为1，当stride=1时，模型的输出特征图可以与输入特征图保持一致；当stride=2时，输出特征图的宽和高都缩小一倍。
5.1.7 使用卷积运算完成图像边缘检测任务
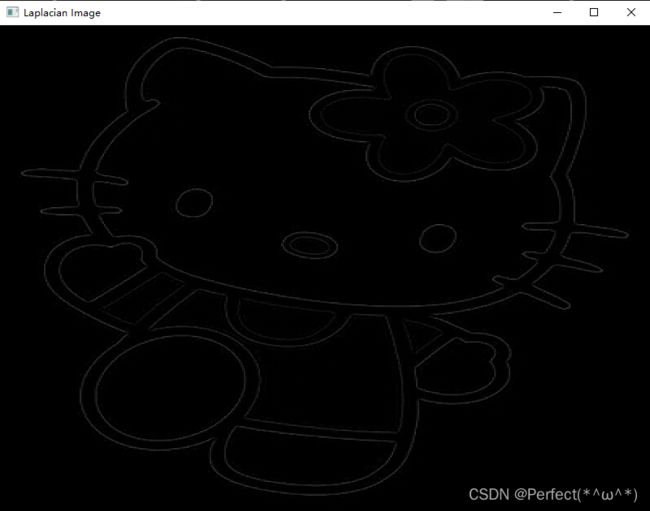
下面我们利用上面定义的Conv2D算子，构造一个简单的拉普拉斯算子，并对一张输入的灰度图片进行边缘检测，提取出目标的外形轮廓。
import torch
import torch.nn as nn
import torch.nn
import numpy as np
class Conv2D(nn.Module):
def __init__(self, kernel_size,stride=1, padding=0):
super(Conv2D, self).__init__()
# 设置卷积核参数
w = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype='float32').reshape((3,3))
w=torch.from_numpy(w)
self.weight = torch.nn.Parameter(w, requires_grad=True)
self.stride = stride
self.padding = padding
def forward(self, X):
# 零填充
new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding])
new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X
u, v = self.weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(
new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * self.weight,
axis=[1, 2])
return output
import matplotlib.pyplot as plt
from PIL import Image
# 读取图片
img = Image.open(r'hello kitty.jpg').convert('L')
img = np.array(img, dtype='float32')
im = torch.from_numpy(img.reshape((img.shape[0],img.shape[1])))
# 创建卷积算子，卷积核大小为3x3，并使用上面的设置好的数值作为卷积核权重的初始化参数
conv = Conv2D(kernel_size=3, stride=1, padding=0)
# 将读入的图片转化为float32类型的numpy.ndarray
inputs = np.array(im).astype('float32')
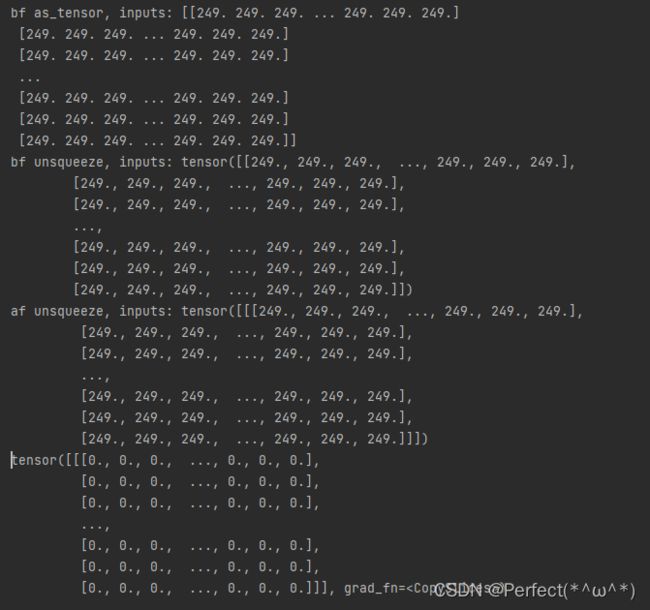
print("bf as_tensor, inputs:",inputs)
# 将图片转为Tensor
inputs = torch.as_tensor(inputs)
print("bf unsqueeze, inputs:",inputs)
inputs = torch.unsqueeze(inputs, axis=0)
print("af unsqueeze, inputs:",inputs)
outputs = conv(inputs)
print(outputs)
# outputs = outputs.data.squeeze().numpy()
# # 可视化结果
plt.subplot(121).set_title('input image', fontsize=15)
plt.imshow(img.astype('uint8'),cmap='gray')
plt.subplot(122).set_title('output feature map', fontsize=15)
plt.imshow(outputs.squeeze().detach().numpy(), cmap='gray')
plt.savefig('conv-vis.pdf')
plt.show()
选做题
1.实现一些传统边缘检测算子，如：Roberts、Prewitt、Sobel、Scharr、Kirsch、Robinson、Laplacian。
边缘检测系列1：传统边缘检测算子 - 飞桨AI Studio
实现一些传统边缘检测算子，如：Roberts、Prewitt、Sobel、Scharr、Kirsch、Robinson、Laplacian
- 图像的边缘指的是灰度值发生急剧变化的位置。
- 在图像形成过程中，由于亮度、纹理、颜色、阴影等物理因素的不同而导致图像灰度值发生突变，从而形成边缘。
- 边缘是通过检查每个像素的邻域并对其灰度变化进行量化的，这种灰度变化的量化相当于微积分里连续函数中方向导数或者离散数列的差分。
import cv2
import numpy as np
# 加载图像
image = cv2.imread(r'hello kitty.jpg', 0)
image = cv2.resize(image, (800, 800))
# 自定义卷积核
# Roberts边缘算子
kernel_Roberts_x = np.array([
[1, 0],
[0, -1]
])
kernel_Roberts_y = np.array([
[0, -1],
[1, 0]
])
# Sobel边缘算子
kernel_Sobel_x = np.array([
[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]])
kernel_Sobel_y = np.array([
[1, 2, 1],
[0, 0, 0],
[-1, -2, -1]])
# Prewitt边缘算子
kernel_Prewitt_x = np.array([
[-1, 0, 1],
[-1, 0, 1],
[-1, 0, 1]])
kernel_Prewitt_y = np.array([
[1, 1, 1],
[0, 0, 0],
[-1, -1, -1]])
# Kirsch 边缘检测算子
def kirsch(image):
m, n = image.shape
list = []
kirsch = np.zeros((m, n))
for i in range(2, m - 1):
for j in range(2, n - 1):
d1 = np.square(5 * image[i - 1, j - 1] + 5 * image[i - 1, j] + 5 * image[i - 1, j + 1] -
3 * image[i, j - 1] - 3 * image[i, j + 1] - 3 * image[i + 1, j - 1] -
3 * image[i + 1, j] - 3 * image[i + 1, j + 1])
d2 = np.square((-3) * image[i - 1, j - 1] + 5 * image[i - 1, j] + 5 * image[i - 1, j + 1] -
3 * image[i, j - 1] + 5 * image[i, j + 1] - 3 * image[i + 1, j - 1] -
3 * image[i + 1, j] - 3 * image[i + 1, j + 1])
d3 = np.square((-3) * image[i - 1, j - 1] - 3 * image[i - 1, j] + 5 * image[i - 1, j + 1] -
3 * image[i, j - 1] + 5 * image[i, j + 1] - 3 * image[i + 1, j - 1] -
3 * image[i + 1, j] + 5 * image[i + 1, j + 1])
d4 = np.square((-3) * image[i - 1, j - 1] - 3 * image[i - 1, j] - 3 * image[i - 1, j + 1] -
3 * image[i, j - 1] + 5 * image[i, j + 1] - 3 * image[i + 1, j - 1] +
5 * image[i + 1, j] + 5 * image[i + 1, j + 1])
d5 = np.square((-3) * image[i - 1, j - 1] - 3 * image[i - 1, j] - 3 * image[i - 1, j + 1] - 3
* image[i, j - 1] - 3 * image[i, j + 1] + 5 * image[i + 1, j - 1] +
5 * image[i + 1, j] + 5 * image[i + 1, j + 1])
d6 = np.square((-3) * image[i - 1, j - 1] - 3 * image[i - 1, j] - 3 * image[i - 1, j + 1] +
5 * image[i, j - 1] - 3 * image[i, j + 1] + 5 * image[i + 1, j - 1] +
5 * image[i + 1, j] - 3 * image[i + 1, j + 1])
d7 = np.square(5 * image[i - 1, j - 1] - 3 * image[i - 1, j] - 3 * image[i - 1, j + 1] +
5 * image[i, j - 1] - 3 * image[i, j + 1] + 5 * image[i + 1, j - 1] -
3 * image[i + 1, j] - 3 * image[i + 1, j + 1])
d8 = np.square(5 * image[i - 1, j - 1] + 5 * image[i - 1, j] - 3 * image[i - 1, j + 1] +
5 * image[i, j - 1] - 3 * image[i, j + 1] - 3 * image[i + 1, j - 1] -
3 * image[i + 1, j] - 3 * image[i + 1, j + 1])
# 第一种方法：取各个方向的最大值，效果并不好，采用另一种方法
list = [d1, d2, d3, d4, d5, d6, d7, d8]
kirsch[i, j] = int(np.sqrt(max(list)))
for i in range(m):
for j in range(n):
if kirsch[i, j] > 127:
kirsch[i, j] = 255
else:
kirsch[i, j] = 0
return kirsch
# 拉普拉斯卷积核
kernel_Laplacian_1 = np.array([
[0, 1, 0],
[1, -4, 1],
[0, 1, 0]])
kernel_Laplacian_2 = np.array([
[1, 1, 1],
[1, -8, 1],
[1, 1, 1]])
# 下面两个卷积核不具有旋转不变性
kernel_Laplacian_3 = np.array([
[2, -1, 2],
[-1, -4, -1],
[2, 1, 2]])
kernel_Laplacian_4 = np.array([
[-1, 2, -1],
[2, -4, 2],
[-1, 2, -1]])
# 5*5 LoG卷积模板
kernel_LoG = np.array([
[0, 0, -1, 0, 0],
[0, -1, -2, -1, 0],
[-1, -2, 16, -2, -1],
[0, -1, -2, -1, 0],
[0, 0, -1, 0, 0]])
# 卷积
output_1 = cv2.filter2D(image, -1, kernel_Prewitt_x)
output_2 = cv2.filter2D(image, -1, kernel_Sobel_x)
output_3 = cv2.filter2D(image, -1, kernel_Prewitt_x)
output_4 = cv2.filter2D(image, -1, kernel_Laplacian_1)
output_5 = kirsch(image)
# 显示锐化效果
image = cv2.resize(image, (800, 600))
output_1 = cv2.resize(output_1, (800, 600))
output_2 = cv2.resize(output_2, (800, 600))
output_3 = cv2.resize(output_3, (800, 600))
output_4 = cv2.resize(output_4, (800, 600))
output_5 = cv2.resize(output_5, (800, 600))
cv2.imshow('Original Image', image)
cv2.imshow('Prewitt Image', output_1)
cv2.imshow('Sobel Image', output_2)
cv2.imshow('Prewitt Image', output_3)
cv2.imshow('Laplacian Image', output_4)
cv2.imshow('kirsch Image', output_5)
# 停顿
if cv2.waitKey(0) & 0xFF == 27:
cv2.destroyAllWindows()
2.实现的简易的 Canny 边缘检测算法。
边缘检测系列2：简易的 Canny 边缘检测器 - 飞桨AI Studio
- 边缘检测是图像处理中一个基础的算法
- 常用的边缘检测算法有 Sobel、Prewitt、Roberts、Canny、Marr-Hildreth 等
算法原理：
Canny 是一个经典的图像边缘检测算法，一般包含如下几个步骤： - 使用高斯模糊对图像进行模糊降噪处理
- 基于图像梯度幅值进行图像边缘增强
- 非极大值抑制处理进行图像边缘细化
- 图像二值化和边缘连接得到最终的结果
import cv2
# 加载图像
image = cv2.imread(r'cat.webp',0)
image = cv2.resize(image,(800,800))
def Canny(image,k,t1,t2):
img = cv2.GaussianBlur(image, (k, k), 0)
canny = cv2.Canny(img, t1, t2)
return canny
image = cv2.resize(image, (800, 600))
cv2.imshow('Original Image', image)
output =cv2.resize(Canny(image,3,50,150),(800,600))
cv2.imshow('Canny Image', output)
# 停顿
if cv2.waitKey(0) & 0xFF == 27:
cv2.destroyAllWindows()
3.复现论文 Holistically-Nested Edge Detection，发表于 CVPR 2015
边缘检测系列3：【HED】 Holistically-Nested 边缘检测 - 飞桨AI Studio
一个基于深度学习的端到端边缘检测模型。
模型结构
- HED 模型包含五个层级的特征提取架构，每个层级中：
- 使用 VGG Block 提取层级特征图
- 使用层级特征图计算层级输出
- 层级输出上采样
- 最后融合五个层级输出作为模型的最终输出：
- 通道维度拼接五个层级的输出
- 1x1 卷积对层级输出进行融合
- 模型总体架构图如下：
4.复现论文 Richer Convolutional Features for Edge Detection，CVPR 2017 发表
边缘检测系列4：【RCF】基于更丰富的卷积特征的边缘检测 - 飞桨AI Studio (baidu.com)
一个基于更丰富的卷积特征的边缘检测模型 【RCF】。
模型架构：
- RCF 与 HED 模型一样，包含五个层级的特征提取架构，同样也是基于 VGG 16 Backbone
- 相比 HED，RCF 模型更加充分利用对象的多尺度和多级信息来全面地执行图像到图像的预测
- RCF 不只是使用了每个层级的输出，而是使用了每个层级中所有卷积层的输出进行融合（Conv + sum）后，作为边缘检测的输入
- 模型结构图如下：
5.【CED】添加了反向细化路径的 HED 模型 - 飞桨AI Studio (baidu.com)
边缘检测系列5：【CED】添加了反向细化路径的 HED 模型 - 飞桨AI Studio (baidu.com)
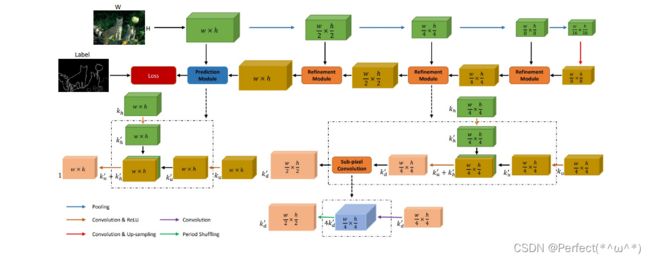
Crisp Edge Detection（CED）模型是前面介绍过的 HED 模型的另一种改进模型：
模型架构
- CED 模型总体基于 HED 模型改造而来，其中做了如下几个改进：
- 将模型中的上采样操作从转置卷积插值更换为 PixelShuffle
- 添加了反向细化路径，即一个反向的从高层级特征逐步往低层级特征的边缘细化路径
- 没有多层级输出，最终的输出为融合了各层级的特征的边缘检测结果
- 架构图如下：
总结:
本次实验主要了解的是二维卷积的相关知识，包括二维卷积的运算、二维卷积的算子以及它的参数量和计数量等，复习了感受野和卷积的变种，通过实验，我对0填充的了解更加透彻。阅读了一些论文并完成了边缘检测。
参考
NNDL 实验5（上） - HBU_DAVID - 博客园 (cnblogs.com)
NNDL 实验5（下） - HBU_DAVID - 博客园 (cnblogs.com)
边缘检测系列1：传统边缘检测算子 - 飞桨AI Studio
边缘检测系列2：简易的 Canny 边缘检测器 - 飞桨AI Studio
边缘检测系列3：【HED】 Holistically-Nested 边缘检测 - 飞桨AI Studio
边缘检测系列4：【RCF】基于更丰富的卷积特征的边缘检测 - 飞桨AI Studio (baidu.com)
边缘检测系列5：【CED】添加了反向细化路径的 HED 模型 - 飞桨AI Studio (baidu.com)