神经网络与深度学习——神经网络基础与反向传播（CS231n）Neural Network Basics & Back Propagation
回顾
之前我们得出了分数函数、损失函数、进而得到数据损失+正则项
我们要得到最好的W，为此使用了梯度下降进行优化。对于梯度下降，有数值法（慢）和解析法（快），在实践中，推导解析梯度，使用数值梯度来检查
但问题是：线性分类并不强
线性分类每类只能学到一个图像，而且只能进行线性决策边界
神经网络
“神经网络”是一个非常宽泛的术语;更准确地说，它们被称为“全连接网络”，有时也被称为“多层感知器”(MLP)
2层3层神经网络可以简单理解为两个三个线性分类器的叠加
注意矩阵相乘时行列的关系
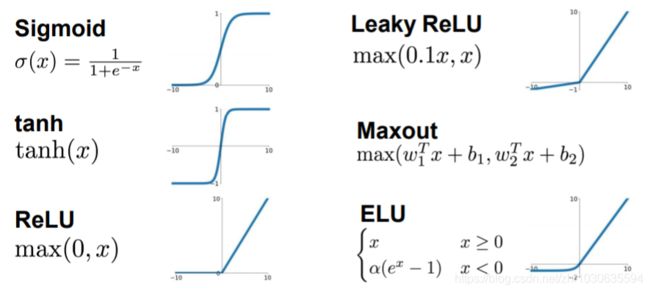
函数 max(0, z) 被称为 激活函数（activation function）
问题 如果尝试建立一个 f = W1W2X 会怎样？
答案 最后还会得到一个线性分类器，因为可以令 W3= W1W2 ，得到 f = W3X
激活函数
其中 ReLU 对大部分问题来说效果还不错
结构
上图为 3层神经网络 或者 2层隐藏层神经网络
其中 hidden layer 与 output layer 为全连接层
神经元越多，拟合能力越强
神经元
人工神经网络的基本计算原理受到神经科学的启发
大脑中的神经元通过被称为动作电位（Action Potentials）的离散脉冲进行交流，然后神经元将这个动作电位传递给它所连接的其他神经元，信息可能被编码在动作电位的速率或时序中。
• 轴突由神经元组成，即神经细胞之细胞本体长出突起，功能为传递细胞本体之动作电位至突触。
• 突触是指一个神经元的冲动传到另一个神经元或传到另一细胞间的相互接触的结构
• 树突为神经元的输入通道，其功能是将自其他神经元所接收的动作电位（电信号）传送至细胞本体。
抽象神经元
当输入信号和模式θ之间的相关性超过某个阈值b时，神经元就会被激活
y = threshold(θ^T - b)
相比于自然的神经网络，这里的神经元分布在有规律的层中，来提高计算效率
神经网络如何工作
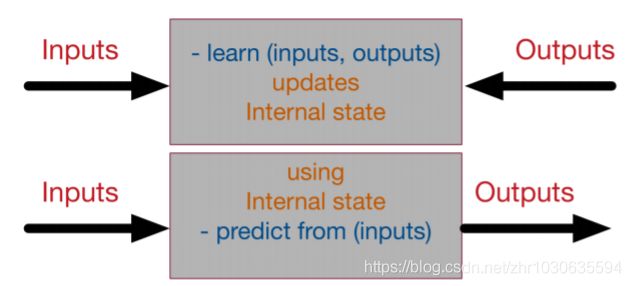
一个监督神经网络可以用一个黑盒模型来表示，该黑盒具有学习和预测两个方式
例子
步骤一：模型初始化
随机初始化，因为不论初始是什么，只要经过学习，就可以达到理想（励志）
例如：
经过学习过程，都可以收敛到理想状态
步骤二：前向反馈
在随机初始化模型后检查其性能，以上面的model 1 为例，可得输出
步骤三：损失函数
我们有了目前模型的输出，也有我们数据的理想输出，所以可求损失函数（衡量神经网络在多大程度上能够达到生成尽可能接近期望值的输出的目标）。
在这里，损失函数取误差的平方和
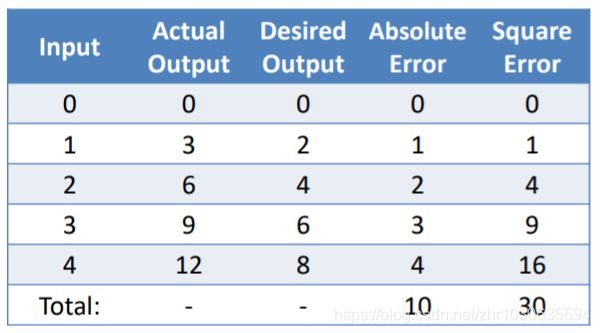
我们的目标是最小化损失函数
步骤四：微分
处理损失函数的导数，一个函数在某一点的导数，给出了这个函数在这一点改变其值的速率
即取一个很小的特定值时，误差变化多少
例如，取 +0.0001
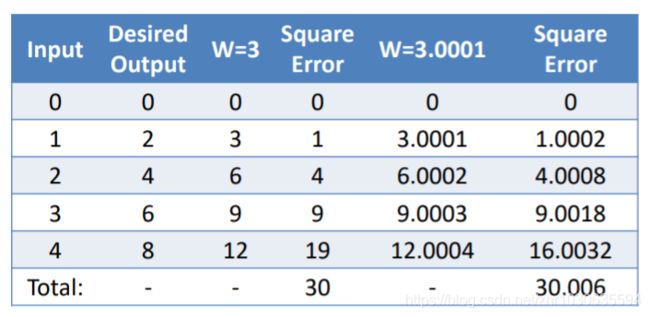
误差变化率 rate = 0.006 / 0.0001 = 60
步骤五：反向传播
在大多数情况下，组合函数是非常困难的
对于每一个组分，我们都要计算组分的导数，幸运的是，导数是可分解的，因此可以反向传播。
如果我们创建一个可微函数库或层库，其中每个函数都知道如何前向传播(通过直接应用函数)和如何后向传播(通过知道函数的导数)，我们就可以构建任何复杂的神经网络。
自动微分
- 只需要在前向传递过程中保存函数调用及其参数的堆栈，就可以知道使用这些函数的导数来反向传播错误的方法
- 通过函数调用反堆积来完成
关于反向传播具体在本文后面讲述
步骤六：权重更新
根据德尔塔定律：
ℎ = ℎ— ∗
- 学习率被引入为一个常数(通常非常小)，以迫使权重得到非常平稳和缓慢的更新(以避免大的步骤和混乱的行为)。
- 如果导率为正，权重的增加会增加误差，因此新的权重应该更小
- 如果导率为负，反之
- 如果导率为0，我们在一个稳定的最小值。因此，不需要更新权值—>已经达到稳定状态
步骤七：迭代直至收敛
每次迭代，更新权重，全局损失函数越来越小
影响迭代次数因素
- 学习率：高学习率意味着更快的学习，但也更不稳定
- 网络的原参数（层数、非线性函数复杂性）：它的变量越多，就需要更多的时间来收敛，但是它可以达到更高的精度
- 优化方式：一些权重更新规则被证明比其他规则更快。
反向传播
反向传播是关于理解在网络中改变权重和偏差是如何改变损失函数的
这里以 (, , ) = ( + ) z 为例，写出其由左到右的计算流程图（上图中绿色数字）。然后由右向左写出其偏导。
如最右边 f / f 时，为 1，必要时熟练使用链式法则
每一步的红色数字 = 上一步的红色数字 * 这一步的偏导（x替换成这一步的绿色数字）
梯度流模式
加号：梯度分配，左边梯度与右边同
乘号：交换乘数
复制：梯度相加
最大：梯度路由