Focal Loss 笔记
2017年ICCV的一篇文章。作者有何凯明、FaceBookAI研究院等。
文章标题:《Focal Loss for Dense Object Detection》
文章地址:https://arxiv.org/abs/1708.02002
Abstract
two-stage 的目标检测器(如 R-CNN 等)通常具有较高精度,这种分类器的目标坐标是稀疏的。
one-stage 检测器作用于规则的、稠密采样的目标坐标,更快更简单,但是精度比 two-stage 的目标检测器低。
本文研究了为什么会出现这种情况。发现主要原因是,在训练密集检测器过程中,遇到极端的前景-背景(正-负)类别不平衡的问题。作者通过改造标准交叉熵损失,来解决这种类别不均衡的问题,降低 loss 中易分类样本的贡献。作者用 Focal Loss 在一组稀疏难样本上训练,防止了在训练过程中,大量的易分类负样本压倒分类器。
为了验证 Focal Loss 的有效性,作者设计了一个简单的叫做 RetinaNet 的稠密检测器,结果表明用 Focal Loss 训练它,能达到 one-stage 的速度,同时达到 two-stage 的精度。
Introduction
在类 R-CNN 的检测器中解决类别不平衡的方法是,通过二阶段级联( tow-stage cascade) 和启发式采样( sampling heuristics) 。在第 1 个阶段 (proposal stage) 中快速地把候选目标坐标的数量缩小 (例如1~2k),过滤掉大部分背景样本。在第 2 个阶段 (classification stage),为了在前景和背景之间维持一个可控制的平衡,执行启发式采样,如固定前景和背景的比例 (1:3) ,或者用在线难样例挖掘 (OHEM)。
相比之下, one-stage 的检测器必须处理大量的,规则采样于一张图片上的候选框。在实践中通常有达到 100,000 多个密集覆盖空间位置、尺度和纵横比的位置。虽然也可以采用类似的启发式采样,但是训练过程仍然被易分类背景样例主导,因此效率低下。这种效率低下是目标检测中的经典问题,人们常用 bootstrapping 或 hard example mining 来解决。
类别不平衡: 无论是经典的 one-stage 检测器(boosted detectors 和 DPMs)还是现代的 one-stage 检测器(SSD)都会面临这个问题。这些检测器在每张图像上评估 1 0 4 10^4 104~ 1 0 5 10^5 105 个候选位置,然而只有少数位置包含目标。
这种不平衡造成两个问题:(1) 训练效率低,大部分坐标都是易分类负样例,带来无用的学习贡献;(2) 大量的易分类负样例会压倒训练,导致模型退化。常用的解决办法是执行难负样例挖掘,而本文通过修改损失函数来解决这个问题。
Focal Loss
Focal Loss 用于解决在 one-stage 检测器训练过程中,前景和背景类的数量存在极端不平衡(例如1:1000)的情况。
先看二分类问题的交叉熵损失(cross entropy, CE ): CE ( p , y ) = { − log ( p ) if y = 1 − log ( 1 − p ) otherwise . \text{CE}(p,y) = \left\{ \begin{array}{ll} -\log(p) & \quad \text{if} \; y =1 \\ -\log(1-p) & \quad \text{otherwise}. \end{array} \right. CE(p,y)={−log(p)−log(1−p)ify=1otherwise.
其中
y ∈ { 1 , 0 } y \in \{1,0\} y∈{1,0} 表示 ground-truth 的标签。
p ∈ [ 0 , 1 ] p \in [0,1] p∈[0,1] 表示模型输出的,估计标签 y = 1 y=1 y=1 的概率。
其实一般写成这样: − 1 N = ∑ n = 1 N [ y n log y ^ n + ( 1 − y n ) log ( 1 − y ^ n ) ] -\dfrac{1}{N} = \sum\limits_{n=1}^N \left[ y_n \log \hat{y}_n + (1-y_n)\log (1- \hat{y}_n) \right] −N1=n=1∑N[ynlogy^n+(1−yn)log(1−y^n)]
其中 y n y_n yn 是标签, y ^ n \hat{y}_n y^n 是网络预测输出。
为了方便表示,我们定义 p t p_t pt: p t = { p if y = 1 1 − p otherwise . p_t = \left\{ \begin{array}{ll} p & \quad \text{if} \; y =1 \\ 1-p & \quad \text{otherwise}. \end{array} \right. pt={p1−pify=1otherwise.
然后重写式子: CE ( p , y ) = CE ( p t ) = − log ( p t ) \text{CE}(p,y) = \text{CE}(p_t) = -\log(p_t) CE(p,y)=CE(pt)=−log(pt)
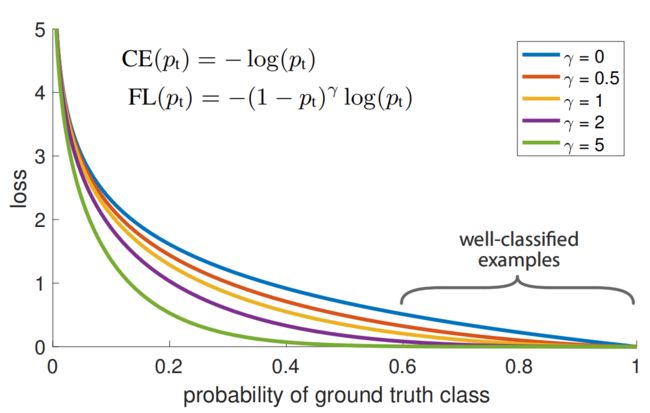
CE 损失如 (图1) 蓝色曲线所示。这种损失有一个显著的特点,可以很容易从图中看出:即使是那些容易分类的样本( p t ≫ 0.5 p_t \gg 0.5 pt≫0.5 的),也会带来不小的损失。当大量的易分类样本加起来后,小的损失也会压倒那些稀少类别(rare class)。
解决类别不平衡的常用方法是引入权重因子 α ∈ [ 0 , 1 ] \alpha \in [0,1] α∈[0,1],对标签 y = 1 y=1 y=1 的类乘以 α \alpha α,对标签 y = 0 y=0 y=0 的类乘以 1 − α 1-\alpha 1−α。在应用时可以通过类频率,或者作为超参数通过交叉验证来设置。为了方便表示,我们定义 α t \alpha_t αt: α t = { α if y = 1 1 − α otherwise . \alpha_t = \left\{ \begin{array}{ll} \alpha & \quad \text{if} \; y =1 \\ 1-\alpha & \quad \text{otherwise}. \end{array} \right. αt={α1−αify=1otherwise.
则此时的 CE 损失为: CE ( p t ) = − α t log ( p t ) \text{CE}(p_t) = -\alpha_t \log(p_t) CE(pt)=−αtlog(pt)
易分类负样本构成了损失的主要部分,主导了梯度。虽然 α \alpha α 平衡了 正 / 负 样例的贡献,但是没有区分 难 / 易 样本。
下面来改造这个损失函数,降低易分类样本的权重,专注难分类负样本的训练。
对交叉熵损失加一个调制因子: ( 1 − p t ) γ \color{red}(1-p_t)^{\gamma} (1−pt)γ,其中 γ ≥ 0 \gamma \geq 0 γ≥0,称为聚焦 (focusing) 参数,是可调的。
所以 Focal Loss 为: FL ( p t ) = − ( 1 − p t ) γ log ( p t ) \text{FL}(p_t) = - (1-p_t)^{\gamma} \log(p_t) FL(pt)=−(1−pt)γlog(pt)
在 (图1) 中展示了 γ \gamma γ 不同取值的图像。
Focal Loss 有 2 个特点 :
(1)当样本被误分类时, p t p_t pt 很小,此时调制因子接近 1 1 1,损失不受影响。
当 p t p_t pt 趋于 1 1 1 时,调制因子趋于 0 0 0,易分类样本对损失的贡献降低了。
(2)聚焦参数 γ \gamma γ 平滑地调节 “易分类样本的贡献率” 。 γ \gamma γ 越大,贡献率越低。
当 γ = 0 \gamma=0 γ=0 时, Focal Loss 和常规的交叉熵损失一样。
当 γ \gamma γ 增大,调制因子的影响也相应地增大。(在作者的实验里 γ = 2 \gamma=2 γ=2 的效果最佳 )
直观地看,调制因子降低了 Loss 中来自易分类样本的贡献,并且把整个低 Loss 的区间拉宽了。
例如当 γ = 2 \gamma=2 γ=2 时, 分类器得到 p t = 0.9 p_t=0.9 pt=0.9 时,比用 CE 算出来的损失要小 100 100 100 倍; p t ≈ 0.968 p_t\approx 0.968 pt≈0.968 时,要小 1000 1000 1000 倍。
这反过来又增加了纠正误分类样本的重要性。(当 γ = 2 \gamma=2 γ=2 , p t ≤ 0.5 p_t\leq0.5 pt≤0.5 时它们的 Loss 最多只被降低了 4 4 4 倍)
(虽然 Loss 都降低了,但是易分类样本的降低得更多)
在应用中会在 Focal Loss 加上 α \alpha α - balanced 变量: FL ( p t ) = − α t ( 1 − p t ) γ log ( p t ) \color{red} \text{FL}(p_t) = - \alpha_t (1-p_t)^{\gamma} \log(p_t) FL(pt)=−αt(1−pt)γlog(pt)
把 Focal Loss 的式子展开容易看点: FL ( p , y ) = { − α ( 1 − p ) γ log ( p ) if y = 1 ( ⅰ ) − ( 1 − α ) p γ log ( 1 − p ) otherwise . ( ⅱ ) \text{FL}(p,y) = \left\{ \begin{array}{ll} -\alpha \; (1-p)^{\gamma} \; \log(p) & \quad \text{if} \; y =1 & \quad (ⅰ)\\[0.5em] -(1-\alpha) \; p^{\gamma} \;\log(1-p) & \quad \text{otherwise}. & \quad (ⅱ) \end{array} \right. FL(p,y)={−α(1−p)γlog(p)−(1−α)pγlog(1−p)ify=1otherwise.(ⅰ)(ⅱ)
p p p 表示模型预测样本为 y = 1 y=1 y=1 的概率。 p ∈ [ 0 , 1 ] p \in [0,1] p∈[0,1], α ∈ [ 0 , 1 ] \alpha \in [0,1] α∈[0,1], γ ≥ 0 \gamma \geq 0 γ≥0。
举个例子,当目标标签 y = 1 y=1 y=1 时:
对于易分类正样本,你的分类器也预测它为正类, p p p 很大,损失用式子 ( ⅰ ) (ⅰ) (ⅰ) 计算。增大 γ \gamma γ 使式子 ( ⅰ ) (ⅰ) (ⅰ) 的值更小,减少它对损失的贡献。
对于易分类负样本,你的分类器也预测它为负类, p p p 很小,损失用式子 ( ⅱ ) (ⅱ) (ⅱ) 计算。增大 γ \gamma γ 使式子 ( ⅱ ) (ⅱ) (ⅱ) 的值更小,减少它对损失的贡献。
整体而言,易分类样本贡献的损失就变小了。
对于难分类的正样本,你的分类器容易把它预测为负类, p p p 很小,实际上损失是用式子 ( ⅰ ) (ⅰ) (ⅰ) 计算,增大 γ \gamma γ 对 ( 1 − p ) γ (1-p)^{\gamma} (1−p)γ 没什么影响。
对于难分类的负样本,你的分类器容易把它预测为正类, p p p 很大,实际上损失是用式子 ( ⅱ ) (ⅱ) (ⅱ) 计算,增大 γ \gamma γ 对 p γ p^{\gamma} pγ 没什么影响。
所以难分类的样本对损失的贡献基本没变。
如果负样本太多,损失函数主要靠式子 ( ⅱ ) (ⅱ) (ⅱ) 计算,那么增加 α \alpha α 就能减少式子 ( ⅱ ) (ⅱ) (ⅱ) 的权重,从而减少负样本的贡献。
综上:
α \alpha α 解决 正 / 负 样本数量不均衡的问题,如果负样本太多,可以适当增加 α \alpha α。
γ \gamma γ 解决 难 / 易 样本数量不均衡的问题,如果易分类的样本太多,可以适当增加 γ \gamma γ。
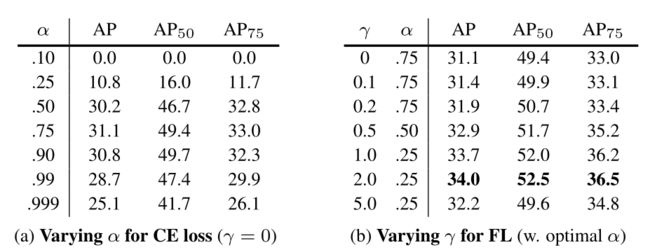
α \alpha α 和 γ \gamma γ 是相互作用的,一般来说 α \alpha α 应该随着 γ \gamma γ 的增加而略有降低, 作者在实验中设置 γ = 2 , α = 0.25 \gamma =2,\alpha=0.25 γ=2,α=0.25 的效果较好 。