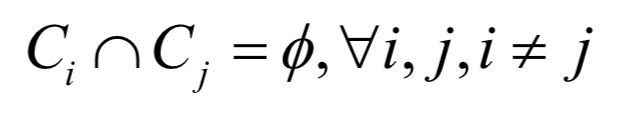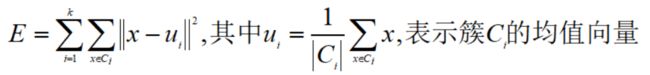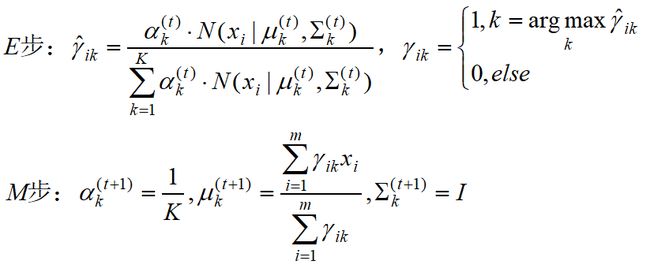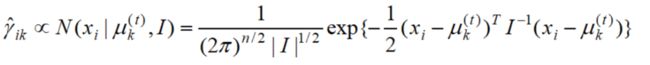聚类算法(K-means)
1.聚类,通俗解释就是物以类聚
2.聚类算法没有训练过程,这是和分类算法最本质的区别
3.K-means是一种最常见的聚类算法,它通过距离定义相似性
4.求解K-means采取启发式的迭代方法5.[_^strong:19171314!]类别个数k和初始质心的选取是影响Kmeans的因素,
6.改进的k-means算法有K-means++,elkanK-means和miniBatchK-means
7.K-means是高斯混合模型的一种特殊情形
从今天起,我们用四篇文章介绍四种聚类算法,包括K-means、DBSCAN、BIRCH和谱聚类。开始之前,先简单介绍一下聚类的定义。
![]()
聚类简介
![]()
聚类,通俗解释就是物以类聚,把同属一个类别的物体聚合在一起。比如小时候玩的课题游戏,把相同的水果放在一堆。本质上就是把相似的样本放在一起,不相似的样本尽可能的分开。
该算法没有训练过程,这是和分类算法最本质的区别,算法要根据自己定义的规则把样本进行分类。
根据此,我们用数学语言对聚类做精确定义:
假设一个样本集C={x1,x2,...,xl},聚类算法把这个样本集划分成m个不相交的子集C1,...,Cm即簇。这些子集的并集是整个样本集:
且每个样本只能属于这些子集中的一个,即任意两个子集之间没有交集:
同一子集内的样本要具备相似性,相似性没有固定的定义,根据不同场景由人工设定。
举个例子,对于样本集C={1,2,3,4,5,6,7,8,9}
按照奇偶性,可以划分为:C1={1,3,5,7,9},C2={2,4,6,8};
按照是否能被3整除,可以分为:C1={1,2,4,5,7,8},C2={3,6,9}
我们把这些样本集合称为簇,显然算法要解决的核心问题是如何定义簇,唯一的要求是簇内的样本尽可能相似。通常我们根据距离和密度来确定,这些往后详细介绍。
![]()
K-means及优化
![]()
K-means是一种最常见的聚类算法,它的原理是:对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。
假设簇划分为{C1,...,Ck},则优化目标是最小化平方误差E:
直接求解非常难,一般采取启发式的迭代方法:
很显然,对于K-means,类别个数k和初始质心的选取将会影响算法的效率。
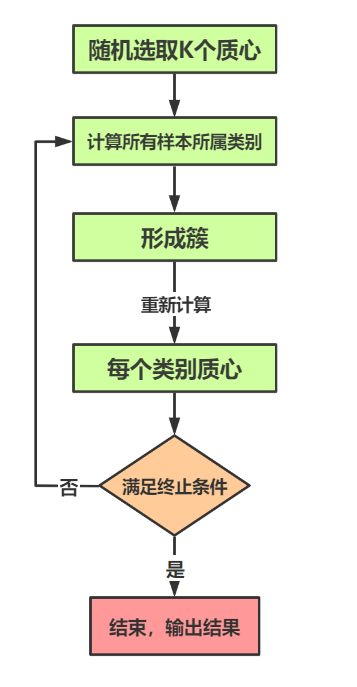
传统K-means算法流程为:
前面提到,初始质心选择的随机性是影响算法迭代效率的原因,针对这个问题,提出了改进的方案——K-means++算法:
我们观察到,每一轮迭代中,要计算所有样本到所有质心的距离,这样耗时,效率较低。针对这个现象,提出了改进方案——elkan K-means和mini Batch K-means
elkan K-means算法的目标是减少不必要的距离的计算。它利用了两边之和大于等于第三边,以及两边之差小于第三边的三角形性质,来减少距离的计算。
如果样本的特征稀疏、有缺失值的话,这个方法就不使用了,此时某些距离无法计算
mini Batch K-means选择一个合适的批样本来做K-Means聚类,该批样本一般通过无放回的随机采样得到
![]()
从K-means到GMM
![]()
K-means是通过距离来度量相似性。实际上,它可以看成高斯混合模型(GMM)的一种特殊情形。
传送门:高斯混合模型(GMM)
我们知道,GMM的算法流程为:
在高斯混合模型中,每个样本可以属于任何分模型,它来自所有模型的加权之和。如果对GMM的条件做一些限制:
每个样本将不再依概率Z~X归属于每个高斯分布,而是每次迭代中每个样本将以概率为1只归属于一个确定的高斯分布(后验概率取值1或0)
各个高斯分布的协方差矩阵为单位矩阵I
隐变量Z为均匀分布, 即样本是等概率从各个高斯分布中采样得到
即GMM特殊形式(K-means)的E步和M步是:
又因为:
所以,后验概率γ中的高斯分布概率密度函数值实际上反比于样本xi与对应高斯分布均值向量u的欧式距离:
所有样本将以概率为1被归于与之欧氏距离最小的均值向量所属的高斯分布
这与K-means算法一致!
K-means算法优缺点
最后,总结一下K-means的优缺点:
K-Means的主要优点有:原理简单易于实现;可解释度较强;调参仅仅是簇数k
K-Means的主要缺点有:K值选取不好把握;非凸的数据集难收敛;异常点较敏感;若类别的数据量失衡,或者各类别方差不同,则聚类效果不佳。
参考资料:
https://mp.weixin.qq.com/s/1SOQZ3fsiYtT4emt4jvMxQ
https://mp.weixin.qq.com/s/FLR36-n126aVbTxjD1MMGQ