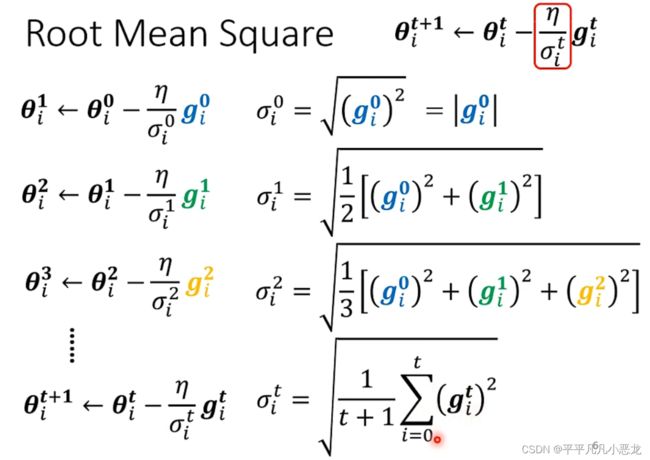DeepLearning-Lihongyi
Class one(09.26)
一：机器学习的任务：
1、regressiong:找到一个函数function，通过输入特征x，输出一个数值scalar
例子：股市预测：输入：过去10年股票的变动、新闻资讯、公司并购咨询等
输出：预测股市明天的平均值
2、Classification:从设定到的种类中，输出属于其中的一种（做选择题）
例子：阿法狗下棋
找到一个函数，在给予19*19个输入棋盘中，选择输出一个位置
3、Structured Learning:如机器画一张图，写一篇文章，让机器产出这种结构性的东西，成为结构学习，即学会创造。
二：机器如何找一个函数呢？
分为三个步骤：
1、写出一个带有未知参数的函数：y =b +w*x1（假设模型 Model）
输入x1与输出y为feature ； b（偏置）与w（权重）成为未知参数，通过训练学习更新数值
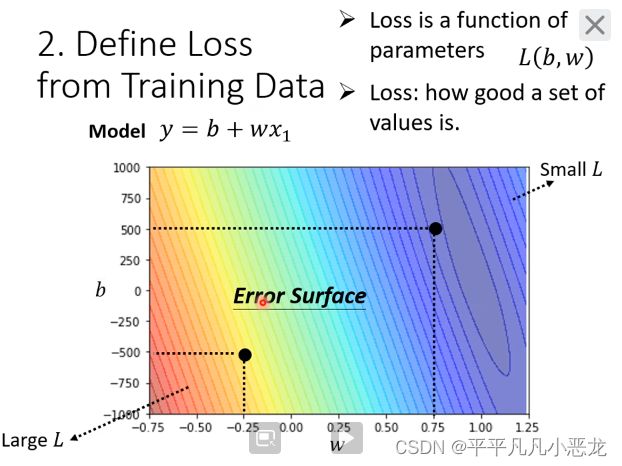
2、从训练集中定义一个Loss函数（成本函数、损失函数） （L(b,w)）
输入为b与w，其作用是看看我们设定未知参数的效果怎么样
误差计算方式取决与我们的需求。
由不同的b跟w值所测绘出的Loss函数等高线图，来直观的看未知参数选值结果对照，越接近蓝色区域效果越好。
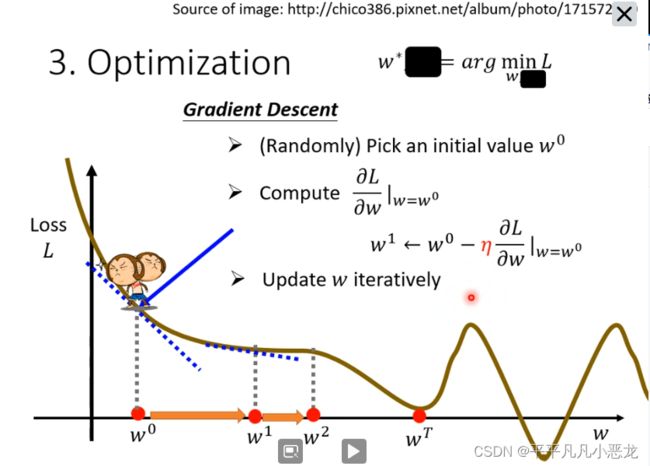
3、Optimization（最优化问题）：找出一个w跟b使得Loss函数最小
（1）先假设只有w未知，从而利用梯度下降法（算微分）来是Loss函数最小 ，每一次移动的步调取决于曲线斜率跟学习率α。斜率愈大或学习率越小，步调越小。
当设定的超参数之一（如求微分的次数）到达阈值后，w不再更新；或者当斜率为0时，不再更行。然而Loss函数为多个位置为零，分为局部最小值（local minima）和全局最小值（global minimal）。
此处采用的梯度下降法存在有local minima 的问题。
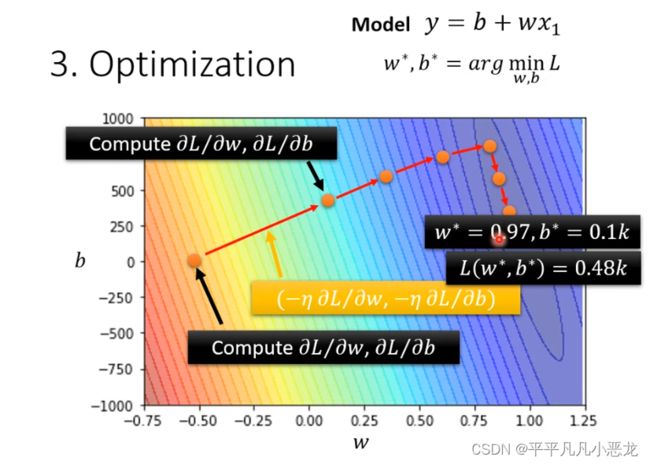
（2）当未知参数有多个时，与一个参数一样，只不过时算其偏微分。
训练集与测试集的结果对比跟优化：
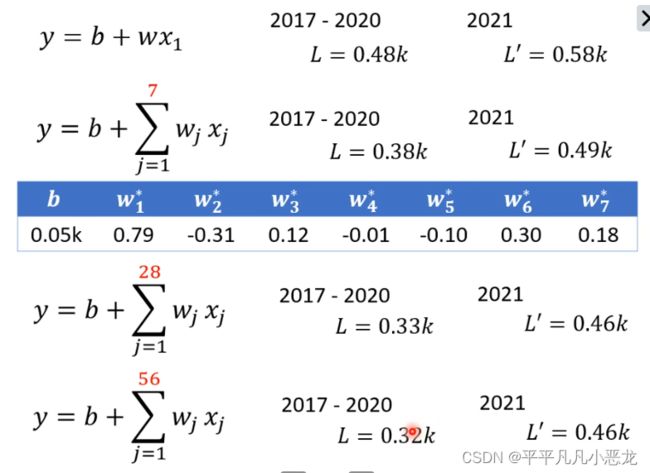
当函数模型改变时，如设置参考预测天数变多，训练集与测试集的表现结果都会有所优化
Class two
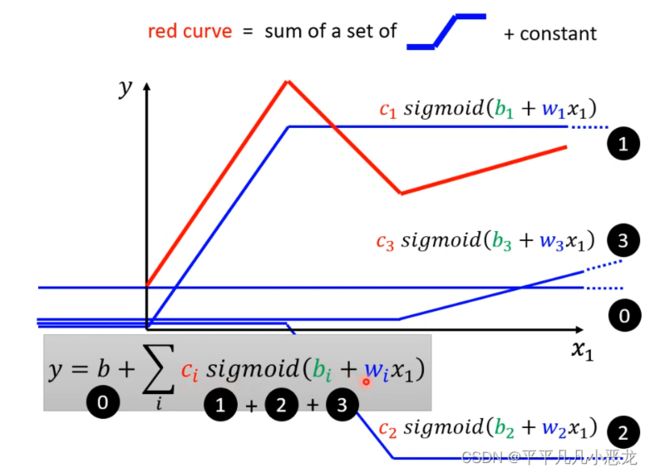
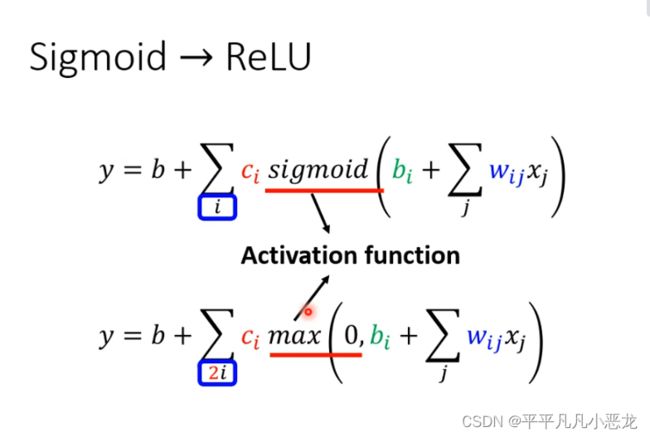
由于前面所使用的模型都是运用线性模型（linear model），对有些复制的问题无法解决（如波折函数），故引进了函数叠加概念，若为曲线问题，可以利用极限思想，叠加无穷个sigmoid函数来拟合。
w：斜率改变 b：函数平移 c：函数高度 （通过修改这三个参数可以得到很多叠加函数来拟合），然后再考虑复杂些的feature，得到新模型：
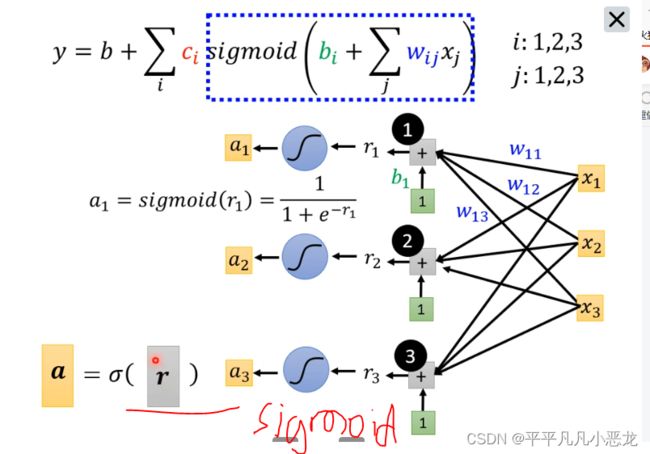
eg：如有三个sigmoid函数，每个函数都有三个feature，在蓝色框中所运行的过程如下图所示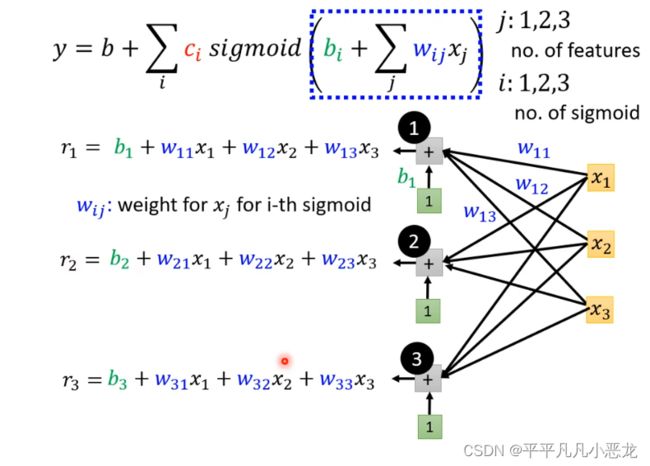
以上计算过程可以利用矩阵乘法进行简化：
计算完后进行的是sigmoid 函数化
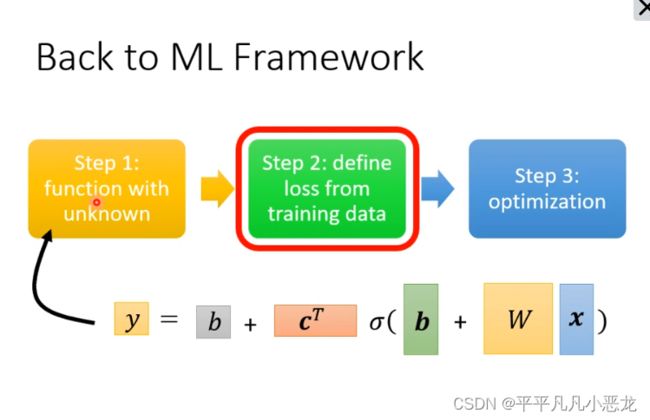
最后分别得出的向量a*c的转置相乘+b得到函数模型
回到深度学习的第一步，得到新的函数模型后进行第二三步：
设置一组初始值代入后计算出y`-y的平均差值后，利用梯度下降法更行各个参数。
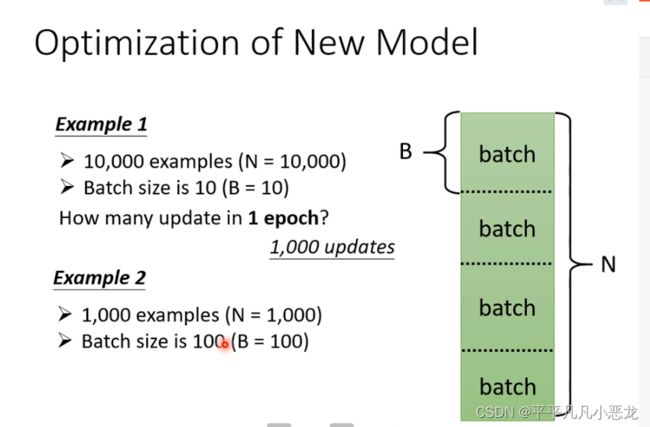
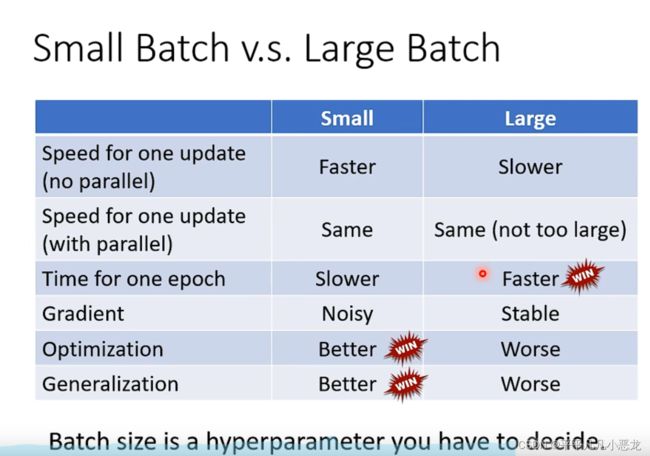
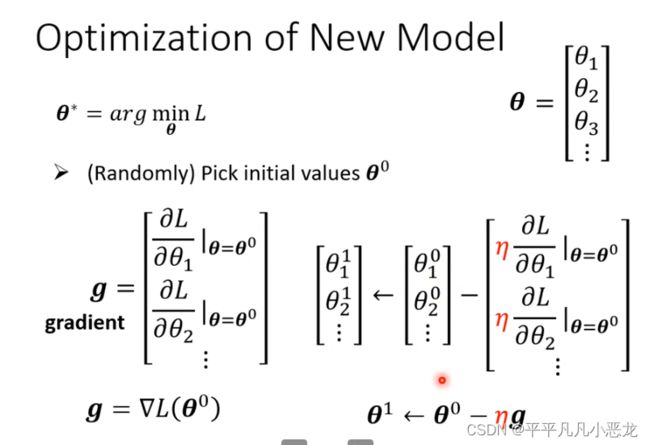直到停下来（g变为0活着计算设定次数达到阈值），除了这种利用全部未知参数组成大向量g得到更新参数向量g`，还可以利用大向量组g分为多个batch（批次），任何一个批次参数更行称为update，所有得批次更新称为一次epoch（纪元）。两者得区别如下例子说明：
当然，激活函数有多种：如sigmoid跟ReLU
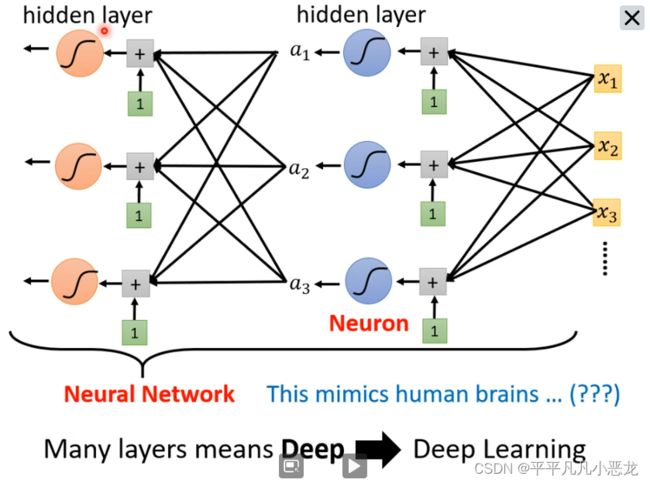
经过多层迭代后可以构成神经网络。
class2（11.21）
1、训练问题
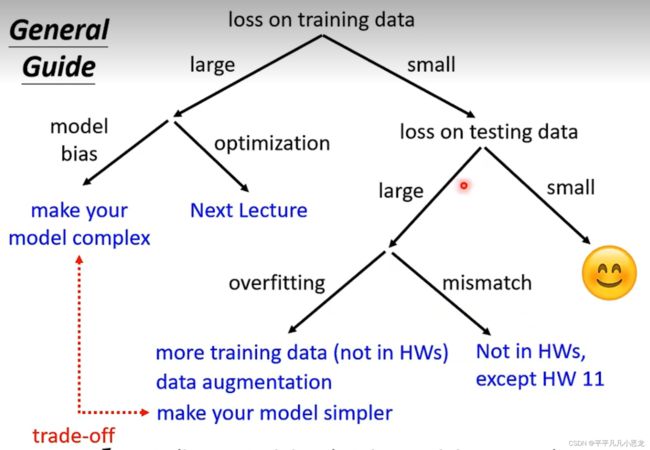
（1）当训练效果不好时，有两种可能性：
Ⅰ：模型太小（层数，学习参数过少）Ⅱ：模型优化存在问题
如何去区分这两种情况？→看训练的损失函数效果：如果层数较浅的网络损失低于层数深的网络，那么可以认定为是情况Ⅱ（optimization存在问题）
（2）当训练效果不错时，我们才需要进一步比较测试效果，测试集损失函数过大时：
Ⅰ：过拟合问题→可以使用数据增强或使用正则化（降低模型弹性）
Ⅱ：欠拟合问题→模型训练不足
2、当模型训练不起来的情况
（1）局部最小值（local minima）与鞍点（saddle point）
当梯度为0时，模型就学习不下去了
利用海森公式可以推断critical point是否为鞍点看，如果是鞍点，则可以从中找出方向继续训练。（在现实模型中，由于模型参数非常高纬度，那么local minima 的情况其实是非常少的）
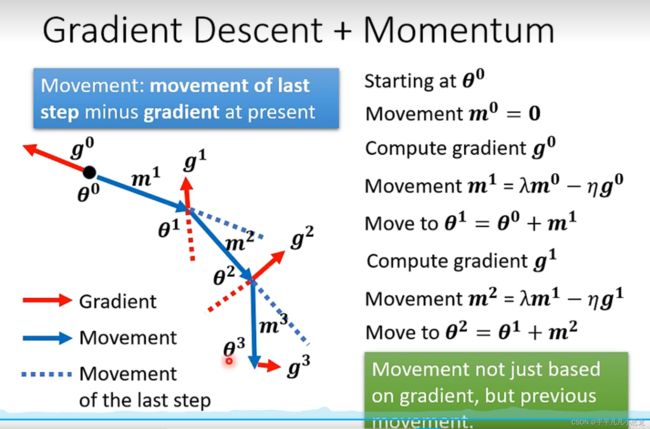
（2）batch_size与momentum的影响
Ⅰ：批量大小
Ⅱ：动量问题：可以当作解决critical point的一种方法（优化算法）
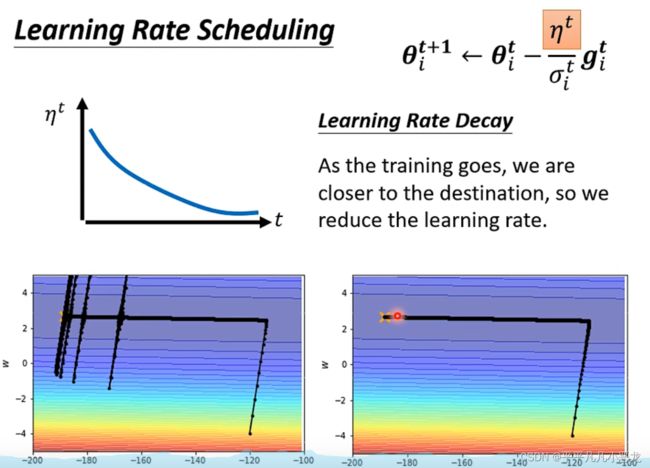
（3）自动调整学习率
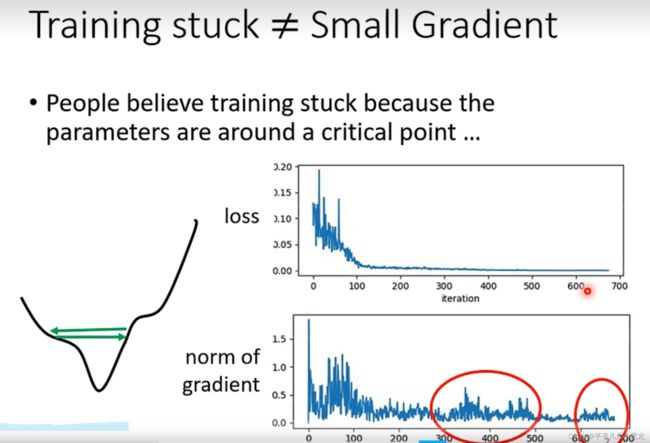
现实训练网络时，常常会遇到loss函数随着迭代次数上升难以下降的问题，其可能的原因大多是不是由于critical point导致的（迭代次数不断增加，此时的梯度还不为0）；其中梯度更行参数learning rate设置错误的原因。之前采用参数都是同个学习步长。然而在gradient数值很小时，我们希望learning rate可以大一些，想法若梯度大了，我们希望步长小些。这样不会卡在某个点。
由上图可见，并非由于critial point导致的loss无法变低
我们所希望的学习率，可以随网络梯度变化而变化，由此，引进均方根。当梯度越大时，
越大，对应的learning rate就越小。
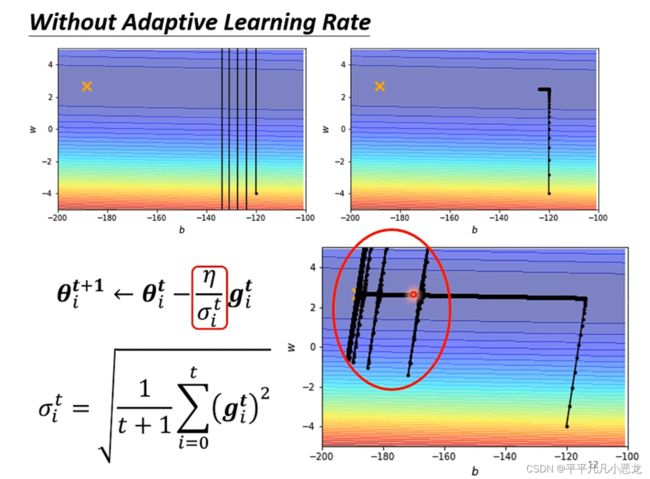
然而即使对于同一个参数，在不同地方（多个维度）也需要进行学习步长的调整，因此引进了RSMProp
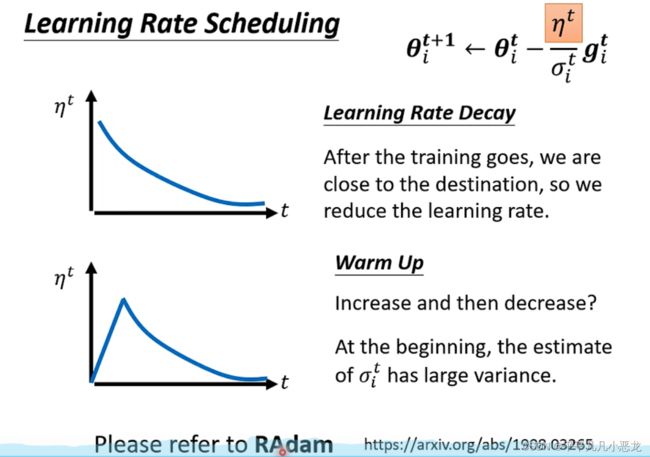
在目前网络的优化中，最常使用的就是Adam：RMSProp +momentum，见下图添加可变学习率后gradient接近了critical point，然后存在很多的纵轴跳动，这是由于在该轴的梯度变化很大，经过长时间积累爆发的原因，此时我们可以通过加入随时间变化的
值来调整。
除了learning rate decay还存在有warm up这种调整η值的办法。（在Resnet和transform都提到）
