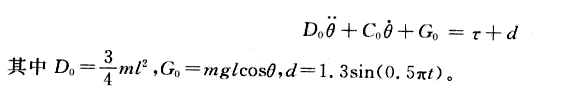Matlab-基于模型不确定补偿的RBF网络机器人自适应控制仿真
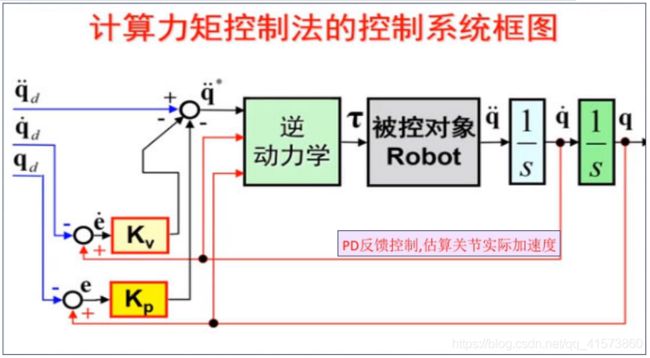
在众多机器人控制算法中,基于模型的计算力矩控制方法是十分有效的,其操作性能也是相当优秀的.然而,这种控制算法必须面对两大难题.第一,必须实现对机器人动力学模型的快速计算第二,必须事先精确了解机器人的动力学模型,因为计算转矩算法在模型未知的情况下鲁棒性较差.但是在实际应用中,即使是获得一个较为理想的机器人动力学模型也是很困难的,另外在操作过程中动力学模型中的各个参数还可能发生变化
神经网络控制
神经网络控制是20世纪80年代以来,在人工神经网络(ANN)研究所取得的突破性进展的基础上,与控制相结和,而发展起来的自动控制领域的前沿学科之一,已成为智能控制的一个新的分支,自学习、自适应性、非线性控制是神经网络控制的特点。
(1)基于精确模型的各种控制结构中充当对象的模型;
(2)在反馈控制系统中直接充当控制器的作用;
(3) 在传统控制系统中起优化计算作用;
(4)在与其它智能控制方法和优化算法相融合中, 为其提供对象模型、 优化参数、推理模型及故障诊断等。
RBF网络
RBF网络是一个具有单隐层的三层前馈网络,如下图,已证明它能以任意精度逼近任一连续函数。 RBF网络模拟了人脑中局部调整、相互覆盖接收域的神经网络结构,因此,是一种局部逼近网络。 采用RBF网络可大大加快学习速度并避免局部极小问题,适合于实时控制的要求。
基本思想:用RBF作为隐单元的 “基”构成隐含层空间,将输入矢量直接(即不需要通过权连接)映射到隐空间当RBF的中心点确定后,映射关系也就确定隐含层空间到输出空间的映射是线性的。
控制仿真
单力臂机械手控制仿真
被控对象:
取m=0.02,l=0.05,g=9.8。
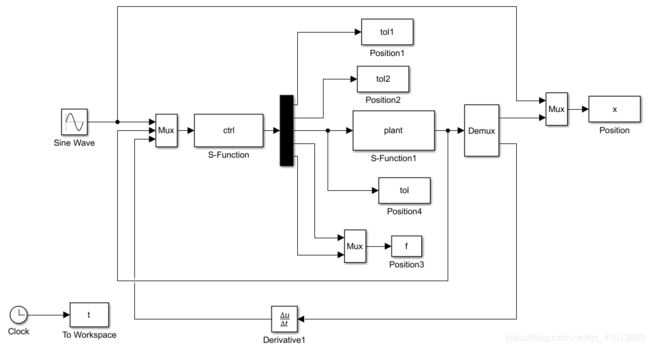
simulink.mdl
控制器子程序ctrl.m
function [sys,x0,str,ts] = spacemodel(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case {2,4,9}
sys=[];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
global c b kp kv
sizes = simsizes;
sizes.NumContStates = 5;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 5;
sizes.NumInputs = 4;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 0;
sys = simsizes(sizes);
x0 = 0.1*ones(1,5);
str = [];
ts = [];
c=0.60*ones(2,5);
b=3.0*ones(5,1);
kp=20;kv=10;
function sys=mdlDerivatives(t,x,u)
global c b kp kv
A=[0 1;
-kp -kv];
B=[0;1];
Q=[50 0;
0 50];
P=lyap(A',Q);
eig(P);
qd=u(1);
dqd=cos(t);
q=u(2);dq=u(3);
e=q-qd;
de=dq-dqd;
xi=[e;de];
h=zeros(5,1);
for j=1:1:5
h(j)=exp(-norm(xi-c(:,j))^2/(2*b(j)*b(j)));
end
gama=150;
Mth=1.0;
th=[x(1) x(2) x(3) x(4) x(5)]';
M1=2;
if M1==1 % Adaptive Law
S=gama*h*xi'*P*B;
elseif M1==2 % Adaptive Law with UUB
k1=0.001;
S=gama*h*xi'*P*B+k1*gama*norm(x)*th;
end
S=S';
for i=1:1:5
sys(i)=S(i);
end
function sys=mdlOutputs(t,x,u)
global c b kp kv
q=u(2);
dq=u(3);
ddq=u(4);
g=9.8;m=1;l=0.25;
D0=4/3*m*l^2;
C0=2.0;
G0=m*g*l*cos(q);
d_D0=0.2*D0;
d_C0=0.2*C0;
d_G0=0.2*G0;
d=1.3*sin(0.5*pi*t);
qd=u(1);
dqd=cos(t);
ddqd=-sin(t);
e=q-qd;
de=dq-dqd;
M=3;
if M==1 %Control for Precise Model
tol1=D0*(ddqd-kv*de-kp*e)+C0*dq+G0;
tol2=0;
tol=tol1;
elseif M==2 %Control with Precise Nonlinear Compensation
f=1/D0*(d_D0*ddq+d_C0*dq+d_G0+d);
tol1=D0*(ddqd-kv*de-kp*e)+C0*dq+G0;
tol2=-D0*f;
tol=tol1+tol2;
elseif M==3 %Control with Neural Compensation
tol1=D0*(ddqd-kv*de-kp*e)+C0*dq+G0;
th=[x(1) x(2) x(3) x(4) x(5)]';
xi=[e;de];
h=zeros(5,1);
for j=1:1:5
h(j)=exp(-norm(xi-c(:,j))^2/(2*b(j)*b(j)));
end
f=1/D0*(d_D0*ddq+d_C0*dq+d_G0+d);
fn=th'*h;
tol2=-D0*fn;
tol=tol1+1*tol2;
end
sys(1)=tol1;
sys(2)=tol2;
sys(3)=tol;
if M==3
sys(4)=f;
sys(5)=fn;
else
sys(4)=0;
sys(5)=0;
end被控对象子程序plant.m
function [sys,x0,str,ts] = spacemodel(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case {2,4,9}
sys=[];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 2;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [0.15;0];
str = [];
ts = [0 0];
function sys=mdlDerivatives(t,x,u) %Time-varying model
g=9.8;
m=1;
l=0.25;
D0=4/3*m*l^2;
d_D0=0.2*D0;
D=D0-d_D0;
C0=2.0;
d_C0=0.2*C0;
C=C0-d_C0;
G0=m*g*l*cos(x(1));
d_G0=0.2*G0;
G=G0-d_G0;
d=1.3*sin(0.5*pi*t);
tol=u;
P=2;
sys(1)=x(2);
if P==1
sys(2)=1/D0*(-C0*x(2)-G0+tol);
elseif P==2
sys(2)=1/D*(-C*x(2)-G+tol+d);
end
function sys=mdlOutputs(t,x,u)
sys(1)=x(1);
sys(2)=x(2);绘图子程序plot.m
close all;
figure(1);
plot(t,x(:,1),'r',t,x(:,2),'b');
xlabel('time(s)');ylabel('position tracking');
figure(2);
plot(t,tol1(:,1),'r');
xlabel('time(s)');ylabel('tol1');
figure(3);
plot(t,tol2(:,1),'r');
xlabel('time(s)');ylabel('tol2');
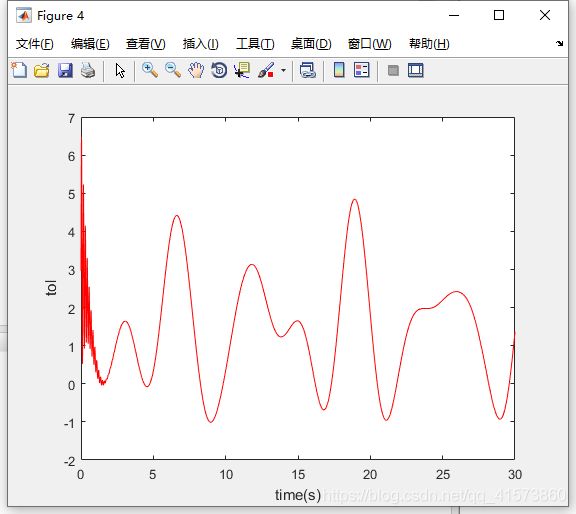
figure(4);
plot(t,tol(:,1),'r');
xlabel('time(s)');ylabel('tol');
figure(5);
plot(t,f(:,1),'r',t,f(:,2),'b');
xlabel('time(s)');ylabel('f and fn');位置跟踪
针对名义模型的控制输入
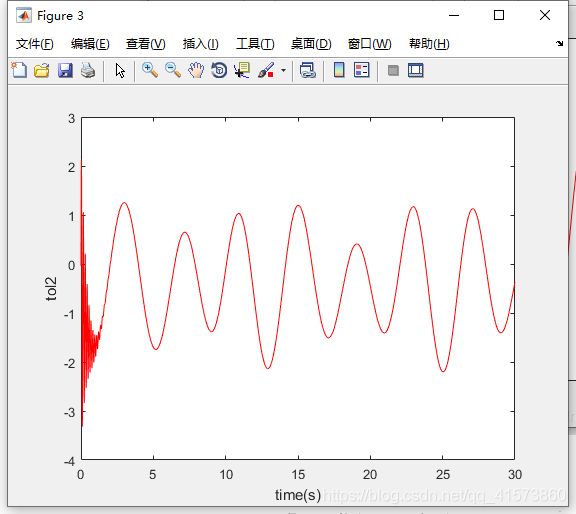
基于神经网络的控制补偿
总的控制输入
建模项及其估计
双力臂机械手控制
双力臂的simulink程序
输入子程序
function [sys,x0,str,ts] = spacemodel(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case {2,4,9}
sys=[];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 2;
sizes.NumInputs = 0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [0 0];
function sys=mdlOutputs(t,x,u)
qd1=1+0.2*sin(0.5*pi*t);
qd2=1-0.2*cos(0.5*pi*t);
sys(1)=qd1;
sys(2)=qd2;控制器子程序
function [sys,x0,str,ts] = spacemodel(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case {2,4,9}
sys=[];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
global c b kv kp
sizes = simsizes;
sizes.NumContStates = 10;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 6;
sizes.NumInputs = 8;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = 0.1*ones(1,10);
str = [];
ts = [0 0];
%c=0.60*ones(4,5);
c= [-2 -1 0 1 2;
-2 -1 0 1 2;
-2 -1 0 1 2;
-2 -1 0 1 2];
b=3.0*ones(5,1);
alfa=3;
kp=[alfa^2 0;
0 alfa^2];
kv=[2*alfa 0;
0 2*alfa];
function sys=mdlDerivatives(t,x,u)
global c b kv kp
A=[zeros(2) eye(2);
-kp -kv];
B=[0 0;0 0;1 0;0 1];
Q=[50 0 0 0;
0 50 0 0;
0 0 50 0;
0 0 0 50];
P=lyap(A',Q);
eig(P);
qd1=u(1);
d_qd1=0.2*0.5*pi*cos(0.5*pi*t);
qd2=u(2);
d_qd2=0.2*0.5*pi*sin(0.5*pi*t);
q1=u(3);dq1=u(4);q2=u(5);dq2=u(6);
e1=q1-qd1;
e2=q2-qd2;
de1=dq1-d_qd1;
de2=dq2-d_qd2;
th=[x(1) x(2) x(3) x(4) x(5);x(6) x(7) x(8) x(9) x(10)]';
xi=[e1;e2;de1;de2];
h=zeros(5,1);
for j=1:1:5
h(j)=exp(-norm(xi-c(:,j))^2/(2*b(j)*b(j)));
end
gama=20;
M1=1;
if M1==1 % Adaptive Law
S=gama*h*xi'*P*B;
elseif M1==2 % Adaptive Law with UUB
k1=0.001;
S=gama*h*xi'*P*B+k1*gama*norm(x)*th;
end
S=S';
for i=1:1:5
sys(i)=S(1,i);
sys(i+5)=S(2,i);
end
function sys=mdlOutputs(t,x,u)
global c b kv kp
qd1=u(1);
d_qd1=0.2*0.5*pi*cos(0.5*pi*t);
dd_qd1=-0.2*(0.5*pi)^2*sin(0.5*pi*t);
qd2=u(2);
d_qd2=0.2*0.5*pi*sin(0.5*pi*t);
dd_qd2=0.2*(0.5*pi)^2*cos(0.5*pi*t);
dd_qd=[dd_qd1;dd_qd2];
q1=u(3);dq1=u(4);
q2=u(5);dq2=u(6);
ddq1=u(7);ddq2=u(8);
ddq=[ddq1;ddq2];
e1=q1-qd1;
e2=q2-qd2;
de1=dq1-d_qd1;
de2=dq2-d_qd2;
e=[e1;e2];
de=[de1;de2];
v=13.33;
q01=8.98;
q02=8.75;
g=9.8;
D0=[v+q01+2*q02*cos(q2) q01+q02*cos(q2);
q01+q02*cos(q2) q01];
C0=[-q02*dq2*sin(q2) -q02*(dq1+dq2)*sin(q2);
q02*dq1*sin(q2) 0];
G0=[15*g*cos(q1)+8.75*g*cos(q1+q2);
8.75*g*cos(q1+q2)];
dq=[dq1;dq2];
tol1=D0*(dd_qd-kv*de-kp*e)+C0*dq+G0;
d_D=0.2*D0;
d_C=0.2*C0;
d_G=0.2*G0;
d1=2;d2=3;d3=6;
d=[d1+d2*norm([e1,e2])+d3*norm([de1,de2])];
%d=[20*sin(2*t);20*sin(2*t)];
f=inv(D0)*(d_D*ddq+d_C*dq+d_G+d);
xi=[e1;e2;de1;de2];
h=zeros(5,1);
for j=1:1:5
h(j)=exp(-norm(xi-c(:,j))^2/(2*b(j)*b(j)));
end
M=3;
if M==1 %Nominal model based controller
tol=tol1;
elseif M==2 %Modified computed torque controller
tol2=-D0*f;
tol=tol1+tol2;
elseif M==3 %RBF compensated controller
th=[x(1) x(2) x(3) x(4) x(5);x(6) x(7) x(8) x(9) x(10)]';
fn=th'*h;
tol2=-D0*fn;
tol=tol1+1*tol2;
end
sys(1)=tol(1);
sys(2)=tol(2);
sys(3)=f(1);
sys(4)=fn(1);
sys(5)=f(2);
sys(6)=fn(2);被控对象子程序
%S-function for continuous state equation
function [sys,x0,str,ts]=s_function(t,x,u,flag)
switch flag,
%Initialization
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
%Outputs
case 3,
sys=mdlOutputs(t,x,u);
%Unhandled flags
case {2, 4, 9 }
sys = [];
%Unexpected flags
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
%mdlInitializeSizes
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 4;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 4;
sizes.NumInputs = 6;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 0;
sys=simsizes(sizes);
x0=[0.6;0.3;0.5;0.5];
str=[];
ts=[];
function sys=mdlDerivatives(t,x,u)
persistent s1 s2
if t==0
s1=0;
s2=0;
end
qd1=1+0.2*sin(0.5*pi*t);
dqd1=0.2*0.5*pi*cos(0.5*pi*t);
qd2=1-0.2*cos(0.5*pi*t);
dqd2=0.2*0.5*pi*sin(0.5*pi*t);
e1=x(1)-qd1;
e2=x(3)-qd2;
de1=x(2)-dqd1;
de2=x(4)-dqd2;
v=13.33;
q1=8.98;
q2=8.75;
g=9.8;
D0=[v+q1+2*q2*cos(x(3)) q1+q2*cos(x(3));
q1+q2*cos(x(3)) q1];
C0=[-q2*x(4)*sin(x(3)) -q2*(x(2)+x(4))*sin(x(3));
q2*x(2)*sin(x(3)) 0];
G0=[15*g*cos(x(1))+8.75*g*cos(x(1)+x(3));
8.75*g*cos(x(1)+x(3))];
d_D=0.2*D0;
d_C=0.2*C0;
d_G=0.2*G0;
d1=2;d2=3;d3=6;
d=[d1+d2*norm([e1,e2])+d3*norm([de1,de2])];
%d=20*sin(2*t);
tol(1)=u(1);
tol(2)=u(2);
dq=[x(2);x(4)];
ddq=[s1;s2];
f=inv(D0)*(d_D*ddq+d_C*dq+d_G+d);
S=inv(D0)*(tol'-C0*dq-G0)+1*f;
sys(1)=x(2);
sys(2)=S(1);
sys(3)=x(4);
sys(4)=S(2);
s1=S(1);
s2=S(2);
function sys=mdlOutputs(t,x,u)
sys(1)=x(1);
sys(2)=x(2);
sys(3)=x(3);
sys(4)=x(4);
绘图子程序
close all;
figure(1);
plot(t,x1(:,1),'r',t,x1(:,2),'b');
xlabel('time(s)');ylabel('position tracking for link 1');
figure(2);
plot(t,x2(:,1),'r',t,x2(:,2),'b');
xlabel('time(s)');ylabel('position tracking for link 2');
figure(3);
plot(t,tol1(:,1),'r');
xlabel('time(s)');ylabel('control input of link 1');
figure(4);
plot(t,tol2(:,1),'r');
xlabel('time(s)');ylabel('control input of link 2');
figure(5);
plot(t,f1(:,1),'r',t,f1(:,2),'b');
xlabel('time(s)');ylabel('f1 and fn1');
figure(6);
plot(t,f2(:,1),'r',t,f2(:,2),'b');
xlabel('time(s)');ylabel('f2 and fn2');
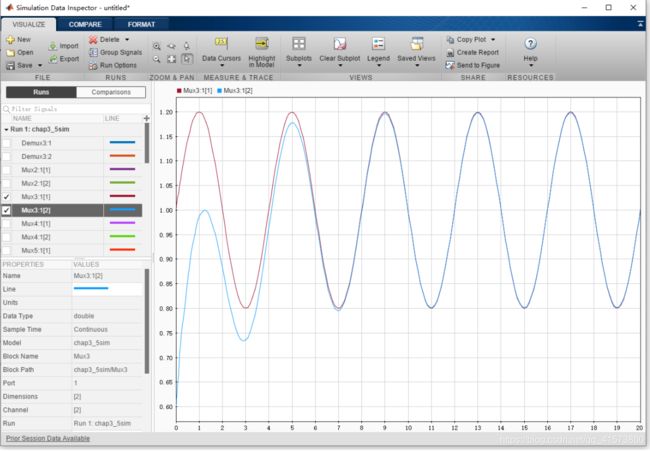
关节1的位置跟踪
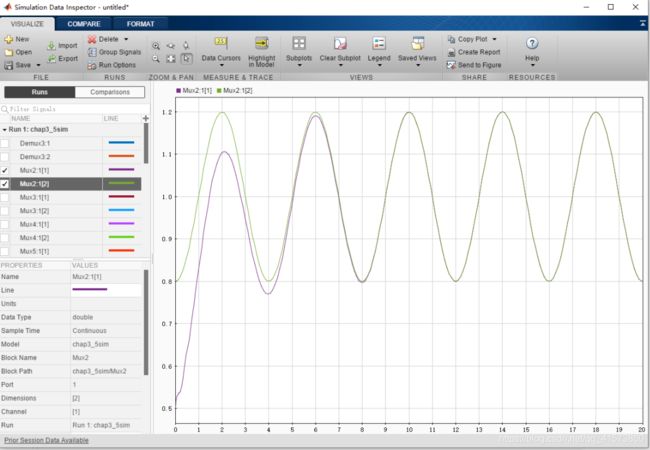
关节2的位置跟踪:
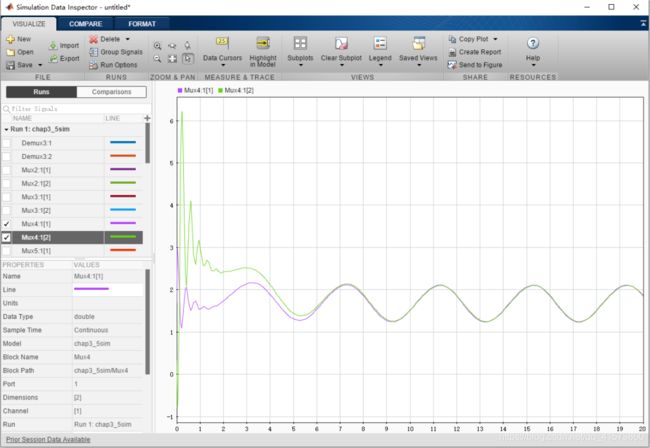
关节1的控制输入
关节2的控制输入
关节1的建模误差及其补偿
关节2的建模误差及其补偿