卷积神经网络CNN---LeNet
LeNet,它是最早发布的卷积神经网络之一,这个模型是识别图像中的手写数字。
论文:Gradient-Based Learning Applied to Document Recognition
年份:1998
一、模型简介:
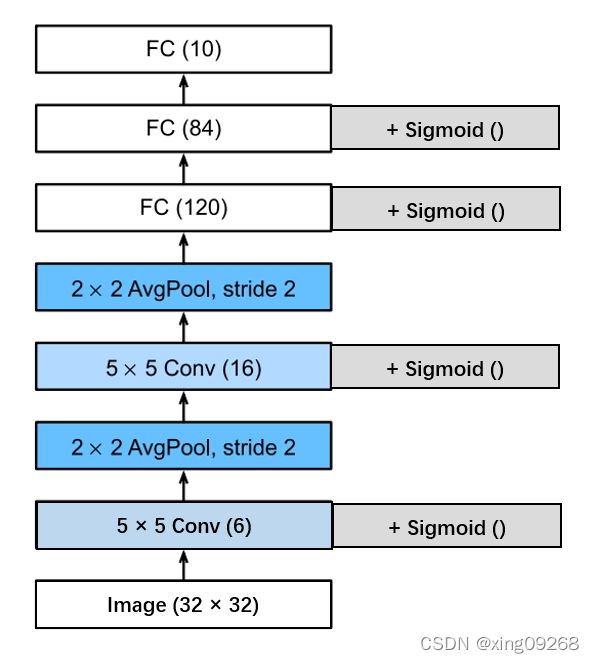
LeNet是一个七层的网络。不包括输入层,输入层的图片是32*32大小。包括有两个卷积层,标记为C;两个池化层,标记为S;三个全连接层,标记为F。
模型的简化图:
网络所采用的激活函数是sigmoid函数。
与卷积核卷积后输出的图片大小计算方式:(输入的尺寸 - 卷积核的尺寸) / 卷积的步长 +1。卷积的步长(stride)表示卷积核每次移动的步数,在不做说明的情况下,移动的步数默认为1。
二、层详细介绍
1、C1卷积层
(1)图片变化
这个是网络的第一层,第一次卷积运算。采用的是6个5*5的卷积核,会得到六个feature map,feature map的大小是(32-5)/ 1 + 1 = 28。所以经过第一层卷积后得到的是6个28*28的特征图。
(2)参数计算
应该有6*(5*5+1)=156个参数,在这里卷积核是参数还包括一个偏差。但是从共包括有32*32*156 = 122304个连接数。因为参数共享(也就是卷积核的移动使得参数共享),所以有只需要学习156个参数就可以。
2、S2池化层
(1)图片变化
这个是网络的第二层,第一次池化计算,采用的是 2*2核 平均池化。feature map大小是28/2=14。对C1中的2*2区域内的像素求和乘以一个权重系数后再加上一个偏置,然后将这个结果再做一次映射(即sigmoid)。
(2)参数计算
一个参数和一个偏置,总共六层。所以是(1+1) * 6= 12个参数。总共有5*14*14*6=5880个连接数。
3、C3卷积层
(1)图片变化
这是网络的第三层,第二次卷积计算。采用的是16个5*5的卷积核,得到16个feature map,feature map的大小是(14-5)/1+1=10。所以经过第二次卷积后得到的是16个10*10的特征图。
(2)参数计算
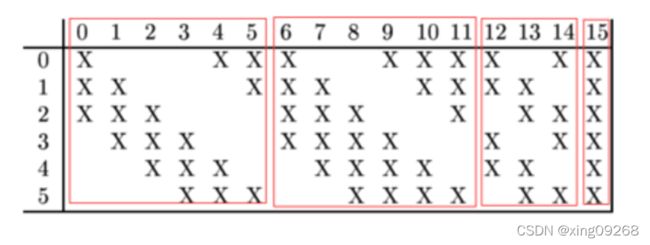
在这里的连接有所不同,因为S2是6个特征图,C3是16个特征图。它们的连接方式是:前六个C3特征映射从S2中三个特征映射的每个连续子集中获取输入。接下来的六个从四个相邻的子集中获取输入。接下来的三个从四个不连续的子集中获取输入。最后一个从所有S2特征映射中获取输入。
采用这样的方式,一个是为了减少参数,二是为了打破对称性以提取多种组合特性。
所以总共有6*(3*5*5+1)+6*(4*5*5+1)+3*(4*5*5+1)+1*(6*5*5+1)=1516个参数。总共有10*10*1516=151600个连接。
4、S4池化层
(1)图片变化
这个是网络的第四层,第二次池化计算,采用的是 2*2核 平均池化。feature map大小是10/2=5。对C1中的2*2区域内的像素求和乘以一个权重系数后再加上一个偏置,然后将这个结果再做一次映射(即sigmoid)。
(2)参数计算
一个参数和一个偏置,总共六层。所以是(1+1) * 6= 12个参数。总共有5*5*5*16=2000个连接数。
5、C5卷积层
因为S4的图片大小是5*5,而这一次又采用了5*5的卷积核,所以得到的特征图的大小是1*1,刚好变成了全连接层。
(1)图片变化
这是网络的第五层,第三次卷积计算。采用的是120个5*5的卷积核,得到120个feature map,feature map的大小是(5-5)/1+1=1。所以经过第二次卷积后得到的是120个1*1的特征图。
(2)参数计算
这里的参数也就是连接数应该是:120*(16*5*5+1)=48120个。
6、F6全连接层
全连接经过Sigmoid函数输出。总共(120+1)*84=10164个参数,也是连接数。
7、F7全连接层
输出10对应的是0~9共十个数字,总共(84+1)*10= 850个参数,也是连接数。
三、总结
LeNet网络是先使用卷积层来学习图片的空间信息,然后使用全连接层来转换到类别空间。
当遇到输入值较大或者网络层数较多的情况,全连接网络所需的参数将会无穷多,卷积神经网络就可以很好的解决这个问题,但是通过LeNet这个模型,我们仍可以发现,参数的重头戏还是在后面的全连接层。
四、参考资料
1、李沐《动手学深度学习》
2、网络解析(一):LeNet-5详解