图像平滑/滤波/模糊

图像平滑（滤波）

一、目标

学会： - 使用各种低通滤镜模糊图像 - 将定制的滤镜应用于图像（2D卷积）

二、2D卷积（图像过滤）

与一维信号一样，还可以使用各种低通滤波器（LPF），高通滤波器（HPF）等对图像进行滤波。LPF有助于消除噪声，使图像模糊等。HPF滤波器有助于在图像中找到边缘。

• OpenCV提供了一个函数cv.filter2D来将内核与图像进行卷积。例如，我们将尝试对图像进行平均滤波。5x5平均滤波器内核如下所示：

$$K=\frac{1}{25}\left[\begin{array}{ccccccccccccccccccccc}1& 1& 1& 1& 11& 1& 1& 1& 11& 1& 1& 1& 11& 1& 1& 1& 11& 1& 1& 1& 1\end{array}\right]$$

• 操作如下:保持这个内核在一个像素上，将所有低于这个内核的25个像素相加，取其平均值，然后用新的平均值替换中心像素。它将对图像中的所有像素继续此操作。试试这个代码，并检查结果:

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('1.jpg')
kernel = np.ones((5, 5), np.float32) / 25
dst = cv.filter2D(img, -1, kernel)
plt.subplot(121), plt.imshow(img), plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(dst), plt.title('Averaging')
plt.xticks([]), plt.yticks([])
plt.show()

三、图像模糊（图像平滑）

通过将图像与低通滤波器内核进行卷积来实现图像模糊。这对于消除噪音很有用。它实际上从图像中消除了高频部分（例如噪声，边缘）。因此，在此操作中边缘有些模糊。（有一些模糊技术也可以不模糊边缘）。OpenCV主要提供四种类型的模糊技术。

1.平均

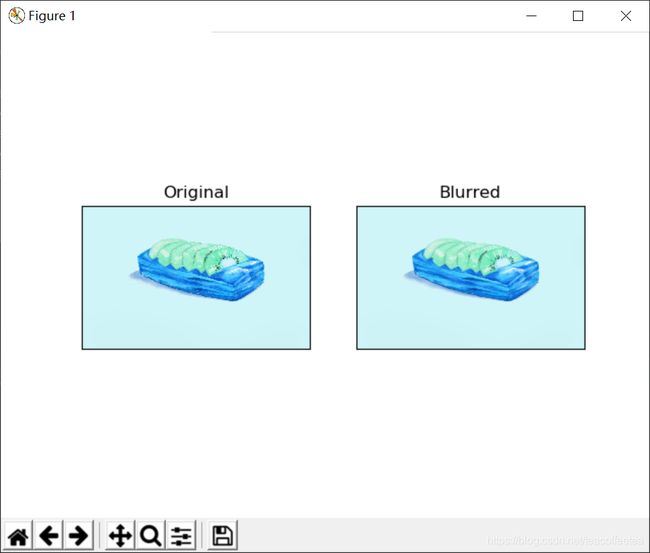
这是通过将图像与归一化框滤镜进行卷积来完成的。它仅获取内核区域下所有像素的平均值，并替换中心元素。这是通过功能cv.blur()或cv.boxFilter()完成的。检查文档以获取有关内核的更多详细信息。我们应该指定内核的宽度和高度。3x3归一化框式过滤器如下所示：

$$K=\frac{1}{9}\left[\begin{array}{ccccccc}1& 1& 11& 1& 11& 1& 1\end{array}\right]$$

注意 如果您不想使用标准化的框式过滤器，请使用cv.boxFilter()。将参数normalize = False传递给函数。

查看下面的示例演示，其内核大小为5x5：

import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('1.jpg')
blur = cv.blur(img, (5, 5))
plt.subplot(121), plt.imshow(img), plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(blur), plt.title('Blurred')
plt.xticks([]), plt.yticks([])
plt.show()

2.高斯模糊

在这种情况下，代替盒式滤波器，使用了高斯核。这是通过功能cv.GaussianBlur() 完成的。我们应指定内核的宽度和高度，该宽度和高度应为正数和奇数。我们还应指定X和Y方向的标准偏差，分别为sigmaX和sigmaY。如果仅指定sigmaX，则将sigmaY与sigmaX相同。如果两个都为零，则根据内核大小进行计算。高斯模糊对于从图像中去除高斯噪声非常有效。

如果需要，可以使用函数cv.getGaussianKernel() 创建高斯内核。

可以修改以上代码以实现高斯模糊：

import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('1.jpg')
blur = cv.GaussianBlur(img, (5, 5), 0)  # 高斯模糊
plt.subplot(121), plt.imshow(img), plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(blur), plt.title('Blurred')
plt.xticks([]), plt.yticks([])
plt.show()

3.中位模糊

在这里，函数cv.medianBlur() 提取内核区域下所有像素的中值，并将中心元素替换为该中值。这对于消除图像中的椒盐噪声非常有效。有趣的是，在上述过滤器中，中心元素是新计算的值，该值可以是图像中的像素值或新值。但是在中值模糊中，中心元素总是被图像中的某些像素值代替。有效降低噪音。其内核大小应为正奇数整数。

在此演示中，我向原始图像添加了50％的噪声并应用了中值模糊。检查结果：

import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('1.jpg')
median = cv.medianBlur(img, 5)  # 中位数模糊
plt.subplot(121), plt.imshow(img), plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(median), plt.title('Median')
plt.xticks([]), plt.yticks([])
plt.show()

4.双边滤波

cv.bilateralFilter() 在去除噪声的同时保持边缘清晰锐利非常有效。但是，与其他过滤器相比，该操作速度较慢。我们已经看到，高斯滤波器采用像素周围的邻域并找到其高斯加权平均值。高斯滤波器仅是空间的函数，也就是说，滤波时会考虑附近的像素。它不考虑像素是否具有几乎相同的强度。它不考虑像素是否是边缘像素。因此它也模糊了边缘，这是我们不想做的。

双边滤波器在空间中也采用高斯滤波器，但是又有一个高斯滤波器，它是像素差的函数。空间的高斯函数确保仅考虑附近像素的模糊，而强度差的高斯函数确保仅考虑强度与中心像素相似的那些像素的模糊。由于边缘的像素强度变化较大，因此可以保留边缘。

以下示例显示了使用双边过滤器（有关参数的详细信息，请访问docs）。

import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('1.jpg')
blur = cv.bilateralFilter(img, 9, 75, 75)
plt.subplot(121), plt.imshow(img), plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(blur), plt.title('Blurred')
plt.xticks([]), plt.yticks([])
plt.show()

参考文档：http://www.woshicver.com/FifthSection/4_4_%E5%9B%BE%E5%83%8F%E5%B9%B3%E6%BB%91/