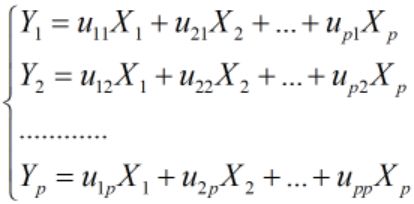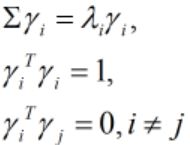pca 累积方差贡献率公式_特征工程 | PCA降维
主成分分析(PCA)是一种多元统计方法，主要利用降维的思想，在损失很少信息的前提下，把多个变量转化为少数几个互不相关的综合变量，各综合变量即称为主成分。简单来说，主成分与原变量之间应有如下关系：
主成分是原变量的线性组合；
各主成分之间互不相关；
主成分的数目远远小于原变量的数目，且保留了原变量绝大多数信息。
假设有p个变量，分别用
表示，随机向量
，设随机向量X的均值为μ，协方差矩阵为Σ。
对X进行线性变换得Y，且
，其中
，
，即：
令 
方差 
，希望
尽可能的大，但需设置
限制条件，才使求的最大值有意义。所以求主成分是在下面约束下的线性变换问题：
- (i=1, 2, ..., p)
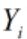和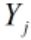
相互无关(i≠j; i, j=1, 2, ..., p)
是所有线性组合中方差最大者；
是与不相关的所有线性组合中方差最大；依次类推，
是与
都不相关的所有线性组合中方差最大者。
假设 
为随机向量X协方差矩阵Σ的特征值，
为各特征值对应的标准正交特征向量。
(1)即有：
做线性变换
(2)主成分方差：
，即主成分方差就是协方差对应的特征值，并有：
.
(3)不同主成分的协方差为：
因而不同主成分是不相关的。
所以，该线性变换满足上述3个约束条件，得到的新变量即为主成分。第一主成分
是将最大特征值
对应的特征向量
作为线性变换系数的X的线性组合，且的方差为；第二主成分
是将第二大特征值
对应的特征向量
作为线性变换系数的X的线性组合，且的方差为；依次类推。也就是说，求主成分问题就变成了求特征值和特征向量的问题。
求主成分既可以从原始数据的协方差矩阵出发求特征值和特征向量进而求得主成分；也可以从原始数据的相关矩阵出发求特征值和特征向量进而求得主成分。后者相当于先对原始数据进行标准化处理，然后求标准化后的数据的协方差矩阵的特征值和特征向量，并且主成分是标准化后的数据的线性组合。
不过，两种方法的使用是有一定差异的。如果各变量的取值范围或量级差异比较大，最好先进行标准化处理，否则直接从原始数据的协方差出发求主成分，取值范围或量级大的变量将在主成分中起主导作用，其他变量将很难在主成分中体现出来。当然标准化处理后，各变量的方差均变为1，会损失一部分信息。如果各变量的取值范围或量级差异较小，可以考虑直接从原始数据的协方差出发求主成分。
主成分的贡献率第k个主成分
的方差贡献率为：
贡献率是主成分的差异占原始数据总差异的比例，贡献率越大，说明主成分对总差异的解释能力越强。
前m个主成分
的累积贡献率为：
累积贡献率用于选择合适的主成分个数，比如当m的取值使累积贡献率达到85%以上时，可以认为是一个比较合适的主成分个数。
例子以python自带iris数据集为例，简单展示scikit-learn的PCA用法。
载入iris数据集：
from sklearn.datasets import load_iris
iris_X = iris.data主成分计算：
from sklearn.decomposition import PCA
pca = PCA(n_components=4)
pca.fit(iris_X)协方差的特征值(主成分的方差)：
# 特征值
pca.explained_variance_
Out[1]: array([4.22484077, 0.24224357, 0.07852391, 0.02368303])主成分方差贡献率：
# 方差贡献率
pca.explained_variance_ratio_
Out[2]: array([0.92461621, 0.05301557, 0.01718514, 0.00518309])累积贡献率：
# 累积贡献率
import numpy as np
np.cumsum(pca.explained_variance_ratio_)
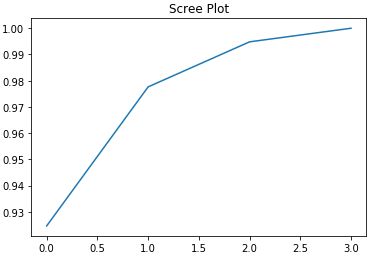
Out[3]: array([0.92461621, 0.97763178, 0.99481691, 1.])由累积贡献率绘制碎石图(scree plot):
# 碎石图
import matplotlib.pyplot as plt
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.title('Scree Plot')
可以看出，前两个主成分解释了原数据97.8%的方差，所以用两个主成分几乎可以完全代替原4个变量。
协方差的特征向量(线性组合的系数)，以下结果每一行对应一个特征向量：
# 特征向量
pca.components_
Out[4]:
array([[ 0.36158968, -0.08226889, 0.85657211, 0.35884393],
[ 0.65653988, 0.72971237, -0.1757674 , -0.07470647],
[-0.58099728, 0.59641809, 0.07252408, 0.54906091],
[ 0.31725455, -0.32409435, -0.47971899, 0.75112056]])主成分(第一列是第一主成分，第二列是第二主成分)：
pca.transform(iris_X)
Out[5]:
array([[-2.68420713e+00, 3.26607315e-01, -2.15118370e-02, 1.00615724e-03],
[-2.71539062e+00, -1.69556848e-01, -2.03521425e-01, 9.96024240e-02],
[-2.88981954e+00, -1.37345610e-01, 2.47092410e-02, 1.93045428e-02],
[-2.74643720e+00, -3.11124316e-01, 3.76719753e-02, -7.59552741e-02],
[-2.72859298e+00, 3.33924564e-01, 9.62296998e-02, -6.31287327e-02]])