算法与程序设计递归算法理解——汉诺塔

目录

1.理解汉诺塔问题可以先从下面两点入手

2.列出一到四层汉诺塔移动顺序寻找规律

3.将移动顺序用树状图来表示

4.将树状图转化为程序实现 

---

1.理解汉诺塔问题可以先从下面两点入手

1. 根据汉诺塔移动规则，移动汉诺塔上层时可视下层为不存在
2. 三个柱子等价

2.列出一到四层汉诺塔移动顺序寻找规律

图2.1汉诺塔模型

一层汉诺塔：A->C

二层汉诺塔：A->B,A->C,B->C

三层汉诺塔；A->C,A->B,C->B,A->C,B->A,B->C,A->C

四层汉诺塔：

A->B,A->C,B->C,A->B,C->A,C->B,A->B,A->C,B->C,B->A,C->A,B->C,A->B,A->C,B->C

处理一下变为:

一层汉诺塔：A->C

二层汉诺塔：A->B,(A->C),B->C

三层汉诺塔；A->C,(A->B),C->B,|(A->C)|,B->A,(B->C),A->C

四层汉诺塔：  

A>B,(A->C),B->C,|(A->B)|,C->A,(C->B),A->B,|(A->C)|,B->C,(B->A),C->A,|(B->C)|,

A->B,(A->C),B->C

我们可以发现n层汉诺塔括号内的移动是n-1层汉诺塔的移动中出现的；且若以|作为分隔，若将移动看为一个向量，不难得到新出现的移动为已出现移动的向量展开.

如：二层时+=

3.将移动顺序用树状图来表示

图3.1两层汉诺塔移动

图3.2三层汉诺塔的移动

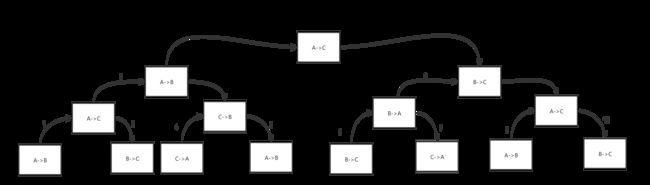
图3.3四层汉诺塔的移动

根据图3.3分析，处于底部的移动为较小圆盘的移动，从底部到顶部圆盘大小逐渐变大，层数为四层（若将最底层整层移走，图将变为三层汉诺塔的移动树状图。如图3.2所示）

从一层到四层移动树状图，树状图以向量展开的形式向下延展，与之相对应的是逐渐给A柱上向上增加小圆盘，所以n层汉诺塔的移动可简化为n-1层汉诺塔的移动，最终简化为2层汉诺塔移动的实现（上层移动可视下层不存在）。

以向量展开中心作为对称轴切树状图为左右两部分，走有两部分的移动具有等价性（三个柱子等价）若以图3.2为例，以A->C为中心切为左右两部分，左部分实现目标为将2层汉诺塔从A移至B，右部分实现目标为将处于B的两层汉诺塔移至C（此时第三层已经移至C）A,B,C三柱等价，左右部分可以看做是交换了柱子的名字，而移动方式是毫无区别的。如此分隔可运用到各层的向量展开中心对上层汉诺塔移动进行理解

4.将树状图转化为程序实现 

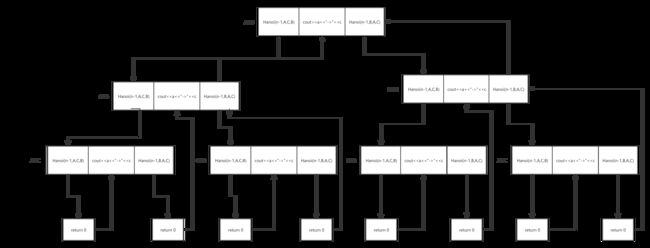
我们可以发现，这种延展方式可以用递归的形式进行实现，如下为三层汉诺塔实现的树状图（可由输入层数来控制递归深度，此时为层数输入为3）

图4.1三层汉诺塔递归实现思路

c++实现

#include 
using namespace std;
int Hanoi(int n,char a,char b,char c)
{
	if(n==0)
		return 0;
	Hanoi(n-1,a,c,b);
	cout<"<>num;
	Hanoi(num,'A','B','C');
	return 0; 
} 

Python实现

def hanoi(n, a, b, c):
    if n == 1:
        print(a, '-->', c)
    else:
        hanoi(n - 1, a, c, b)
        print(a, '-->', c)
        hanoi(n - 1, b, a, c)
# 调用
hanoi(5, 'A', 'B', 'C')

 注：这种分析方式只适用于初学时理解递归如何进行上，对于使用递归时不宜以此方式进行思考