李宏毅老师《机器学习》课程笔记-2.1模型训练技巧

注：本文是我学习李宏毅老师《机器学习》课程 2021/2022 的笔记（课程网站 ），文中图片除了两幅是我自己绘制外，其余图片均来自课程 PPT。欢迎交流和多多指教，谢谢！

Lecture 2 What to do if my network fails to train

1. 模型性能的分析思路

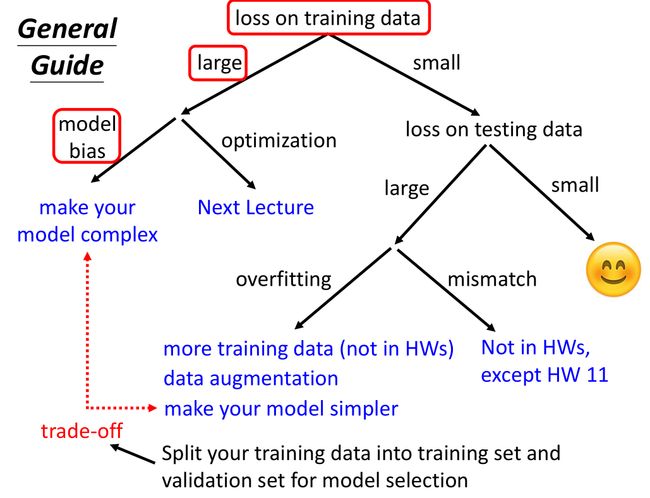
下面的这个树型图写得很详细，按照先看 training loss，再看 testing loss 的步骤，逐个解决 loss 大的问题，直到 training loss 和 testing loss 都小。

按照这个思路，我根据自己的理解，绘制了下面两幅图来分析。

（1）先看 training loss

如果 training loss 大，testing loss 也不会小。为什么？有参考答案的 training data 都没学习好，何况 testing data 是新的数据。

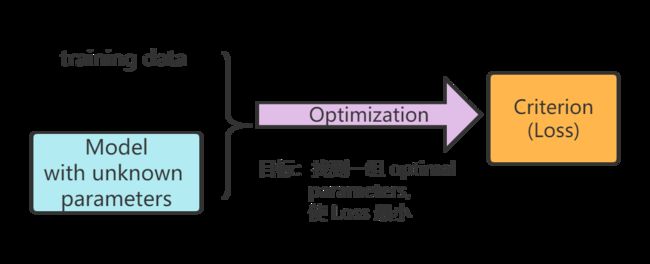
如下图所示，在前一课讲到，在训练中关键的三要素就是：模型 ( Model )、评价标准 ( Loss function )、优化算法 ( Optimization )。对于给定的 training data，如果 training loss 大，就要在 Model 和 Optimization 上找原因，要么是 model bias，要么是 optimization issue。

具体来说：

model bias 指的是模型太简单了，即使是参数集中最小的 loss 都不符合要求（超出了模型的能力范围）。就像在没有针的干草堆里找针，白费功夫。解决办法：增加模型复杂度，比如增加特征，比如增加神经网络的层数。

optimization issue 指的是存在最优参数，但模型没找到。就像在大的干草堆里找针，针是在里面，但是怎么也找不到。解决办法：改进优化策略。本节课剩余内容主要介绍这方面的方法。

启发：之前我以为 training loss 大，就是 model bias，没想到还有一个 optimization 的问题。那么，我们应该如何分辨呢？

对比。可以选一个简单的模型做对比，简单的模型更容易求到优化参数。（这可能也是 baseline 的作用。）如果复杂模型还不如简单模型的性能，那就说明复杂模型没优化好。为什么呢？比如说，用一个 5 层的神经网络，训练出来的 training loss 比用 4 层的神经网络训练的 loss 还要大，就是存在 optimization issue。因为这个 5 层的神经网络，如果最后一层不做任何处理，保持原样输出，就和 4 层的神经网络等效。也就是说，5 层的神经网络起码能达到 4 层神经网络的 loss（有这个能力），现在反而比 4 层的神经网络的 loss 更大，说明没有找到参数最优值（能力没有完全发挥）。

（2）如果 training loss 小，再看 testing loss

如果 testing loss 小，说明模型性能好，万事大吉！

如果 testing loss 大，如下图所示，我们就要从 Model 和 testing data 上找原因。要么是 overfitting，要么是 data mismatch。

overfitting 和 model bias 正相反，model bias 是模型太简单了，overfitting 则是模型太复杂了。overfitting 时，模型对训练集是拟合得好（training loss 小），但是把训练集的细节和噪声也学进去了，得到错误的规律，导致在新数据 ( 如：testing data ) 上表现不佳。解决方法：A. 多收集一些数据。B. 或者做数据扩增 ( data augmentation )，比如把一张图片左右反转得到的图片，如下图所示。C. 或者简化模型，比如做正则化 ( regularization )。

data mismatch 指训练集和测试集数据分布不一致，比如分别是彩色图片和黑白手绘图。需要关注数据的产生（采样）方式。

（3）如何挑选模型？validation set 的作用

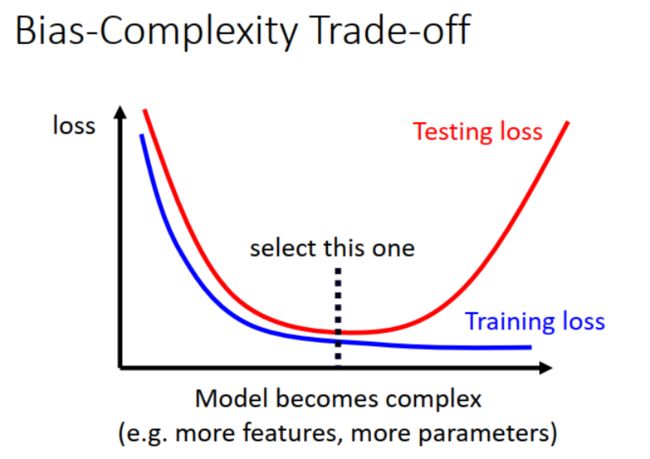
综合上面的分析，我们发现，随着模型复杂度增大， training loss 会逐渐减小至最低，而 testing loss 则会先减小，然后又开始增大。最好能找到中间合适的复杂度，让模型的效果最好，如下图所示：

那么，我们要怎么找到这个合适的复杂度呢？

一个直觉的想法就是训练几个 不同复杂度的模型，看它们在 testing data 的表现，从中选择最好的一个。例如，在 Kaggle 等竞赛平台上，上传结果就可以在 public leaderboard 看到分数。训练几个不同复杂度的模型，把它们在 testing data 的预测结果 $\hat{y}$ 分别上传，从中选择 public leaderboard 分数最好的那一个模型结果作为最终结果。

然而， private leaderboard 一出来，掉榜了！和 public leaderboard 的分数相差挺大，怎么回事？

什么是 public leaderboard 和 private leaderboard？

Kaggle 对 testing data 做了划分（怎么划分的不会告诉你），一部分用作 public leaderboard，提交结果即反馈分数；一部分用作 private leaderboard，比赛结束后才会公布分数。

如果用 public leaderboard 的结果来选模型，无形中就是在学习 public testing set 的信息：哪一种模型在 public testing set 上表现好，我就选哪个。所以，用 private testing set（真正的未知数据）测试，模型的表现不如预期。

这也解释了为什么在公开数据集上，机器在一些任务上（如语音识别）甚至比人类都做得更好。(“This explains why machine usually beats human on benchmark corpora.”) 因为可以根据 public testing set 的结果对模型做调整优化。那么，应用到实际中各种新情况呢，也优于人类吗？

要想让 testing data 反映真实的未知数据，即 public leaderboard 和 private leaderboard 的分数接近，就 不能在模型训练中用 testing data，不只是参数优化时，也包括模型选择时。我觉得，模型选择是指对 同一种类型 的模型，选择不同的复杂度进行比较，确定最佳复杂度。例如，比较神经网络的不同层数。换言之，就是要避免 model bias 或 over fitting。这是我的理解，如果有不对之处，请您多多指教，谢谢！

不能在模型训练中使用 testing data，那要怎么做呢？

把 training data 再划分为 training set 和 validation set，用 validation set 来挑选模型。然后在挑选的模型上运行，把结果上传到 public leaderboard。这样，public leaderboard 的结果就会和 private leaderboard 更为接近。重要的一点是，尽量不要根据 public leaderboard 的结果去调整模型。

万一没划分好，validation set 不好，会影响模型选择啊，怎么办？

采用 N-fold Cross Validation：把数据集划分成 N 份，每次用 N-1 份做 training set，1 份做 validation set。依次做 N 次训练，这样每份数据都有一次作为 validation set。最后取 N 次训练的均值作为模型训练结果，这下不用担心数据集没划分好了。

2. gradient 接近 0，应对办法： batch; momentum

（1）gradient 接近 0 ，不一定是 local minima

gradient 很小，接近 0，是不是 local minima?

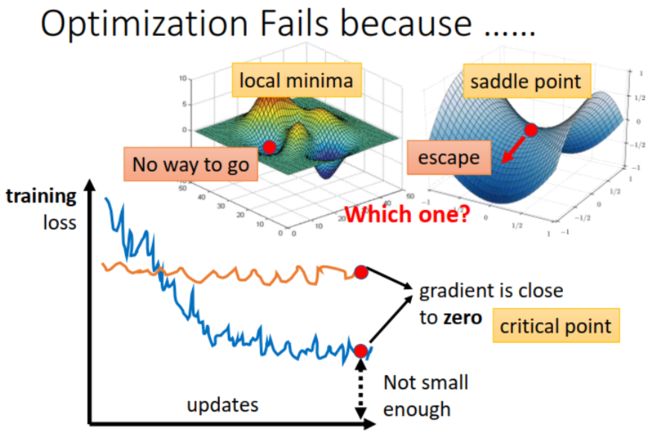
不一定哦，还有可能是 saddle point。这两种 gradient is close to 0 的情况统称为 critical point，如下图所示。

local minima 和 saddle point 有什么不同？

如果到了 local minima，环顾四周，loss 已经是低点，没法下降了，无路可走。而 saddle point 不同，还有路可走。

把 $L(\theta )$ 用泰勒级数展开，如下图所示，Gradient 是一阶导数，Hessian 是二阶导数 。

当 Gradient 接近 0 时，一阶导数项为 0， $L(\theta )$ 可简化为下图所示的表达式，只需看 Hessian 项。可以通过 H 矩阵的 eigen value（特征值），来判断当前的 critical point 属于哪种情况。

怎样走出 saddle point ？

如下图所示，计算 H 矩阵的 eigen values，找到 eigen value < 0 对应的 eigen vector $u$，从而得到参数更新方向 $\theta ={\theta }^{\prime }+u$，这样 loss 可以继续下降。

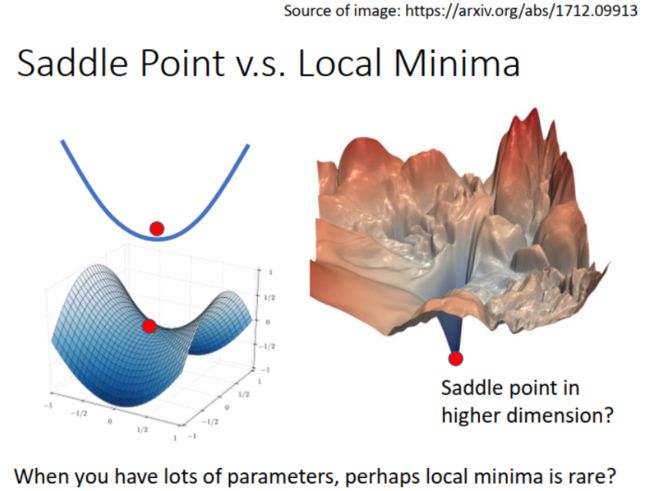
以为到了 local minima，其实不一定：

如下图中左边两幅图所示，在低维看： local minima （高维的一个截面），在高维看：saddle point。低维看觉得无路而走，高维看发现还有路，还可以下降。当模型有很多参数时，维数高，critical point 是 saddle point 的可能性远大于 local minima。因此，很多时候，遇到 critical point，我们以为到了 local minima，其实不然，换条路，loss 还可以继续下降。

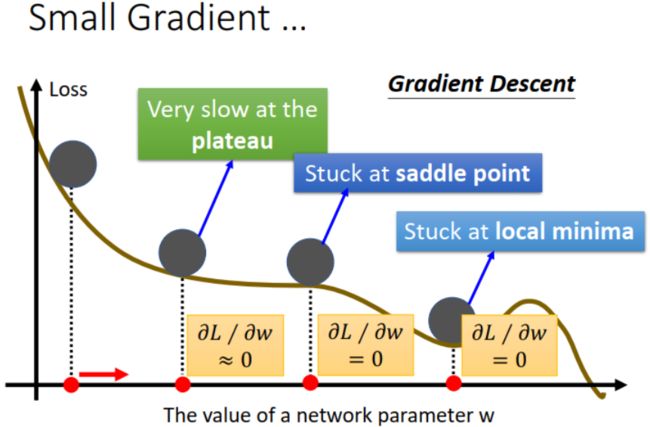
下图中就是我们可能遇到的 gradient 接近 0，loss 不再下降、训练卡住的情况，包括 local minima, saddle point, 或者 loss 曲线十分平缓的情况。实际中一般不会使用前面介绍的计算 Hessian 矩阵和 eigen vector 的方法，运算量太大。那么，遇到 small gradient 怎么办？方法: 提前设置 batch size 和 momentum。接下来依次介绍这两种方法。

（2）small batch v.s. large batch

误解一：small batch 更快。

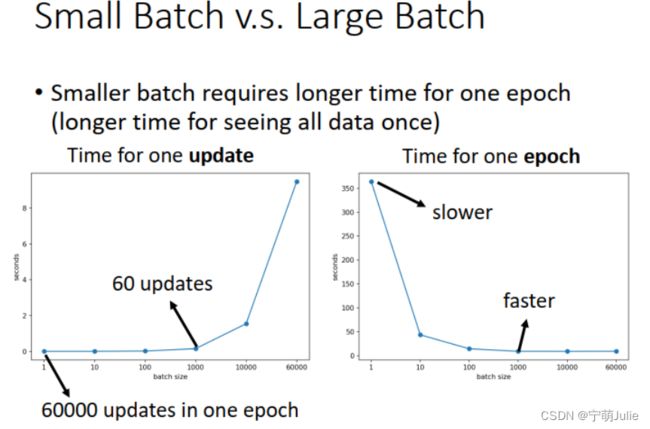
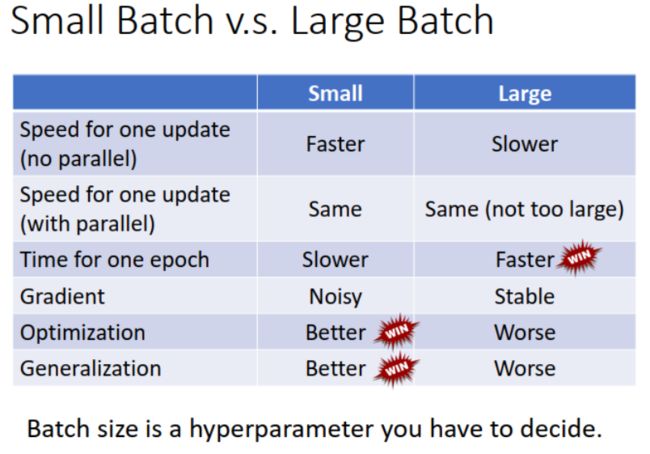
实际上，如果用上 GPU，采用并行计算 ( parallel computing )，large batch 和 small batch 在 1 个 update 的用时差不多。在 1 个 epoch 中，small batch 需要 update 的次数更多，因此耗时更长，如下图所示。

误解二：large batch 用的训练数据更多，看得全面，性能会更好。

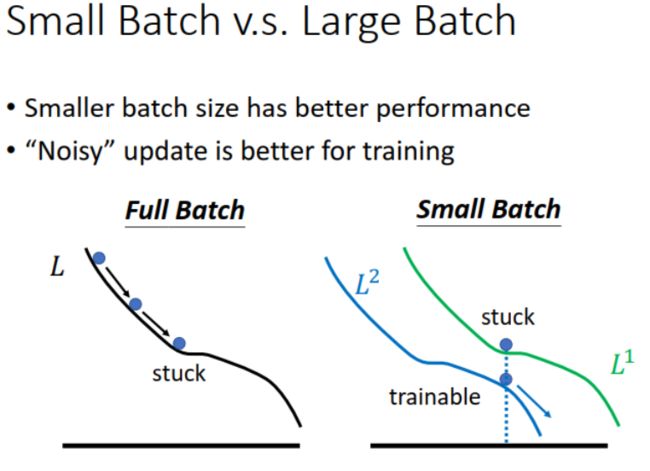
实际上，small batch 训练时不容易卡住：small batch 没有使用所有的训练数据来更新参数，看起来更加 noisy，其实可以避免卡在 critical point。用某个 batch 计算得到的 gradient 接近 0，换一个 batch 计算时，loss 有变化，可能 gradient 就变大了，如下图所示，因此可以继续训练。

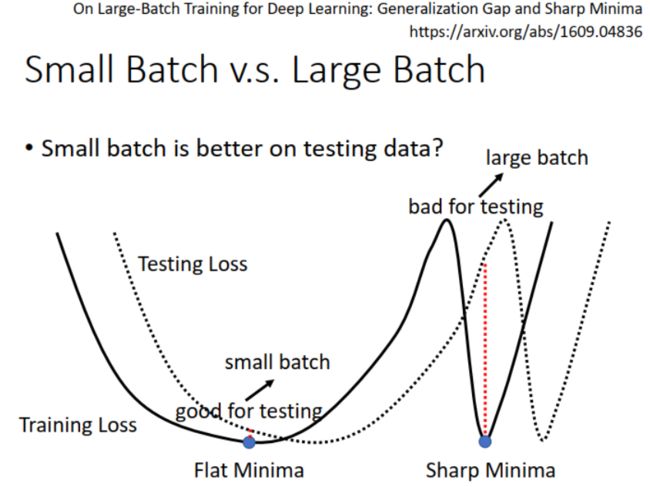
此外，small batch 在 testing set 上的表现更好：一种解释是 small batch 的 local minima 容易是“盆地”形状，而 large batch 的 local minima 容易是“峡谷”形状。如下图所示，当 testing loss 曲线较 training loss 曲线稍有偏移时，采用 small batch 训练得到的模型能够应对，loss 变化不大，而采用 large batch 训练得到的模型，loss 可能就一下子从谷值到峰值，波动很大。

我原以为 small batch 和 large batch 之间的取舍在于是要 small batch 的快，还是要 large batch 的性能。让我完全没想到的是，实际要考虑的是要 small batch 的性能，还是 large batch 的速度，和我设想的正好相反。具体对比如下表所示：

（3）momentum

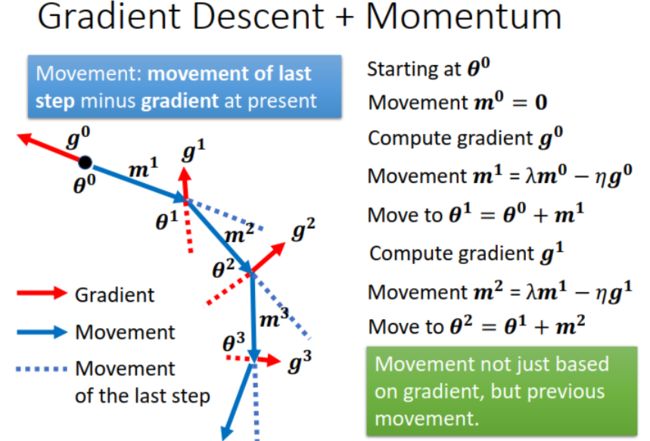
momentum 的思想来源于物理的动量，比如一个小球在斜坡上滚动，遇到小坑（类比：gradient 接近 0 的时候），不会立即停下，而是靠惯性继续前进，从而走出小坑。momentum 综合考虑前一次 update 的 movement 和本次 update 的 gradient。遇到 gradient 接近 0 时，可以凭借之前的动量继续前进，训练不会卡住。

应用 momentum，每一次参数的变化 ( movement ) 不仅与 gradient 有关，还与上一次的变化 ( movement of last step ) 有关，也就是与之前的变化有关。如下图所示：

3. loss 不下降，gradient 却不小，应对办法：adaptive learning rate

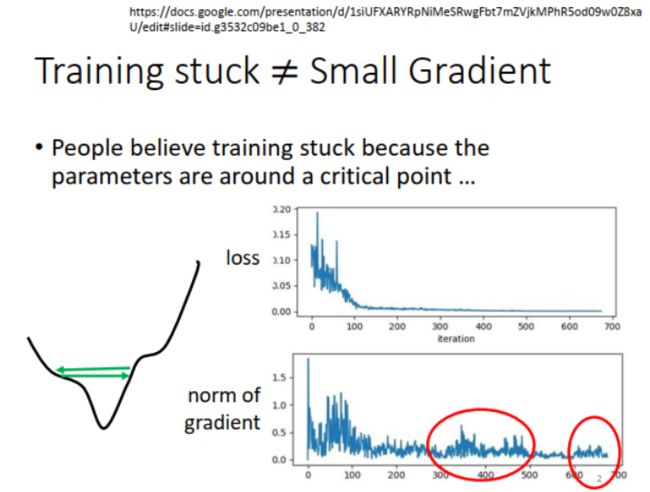
训练卡住，loss 不下降，就是到了 critical point 吗？

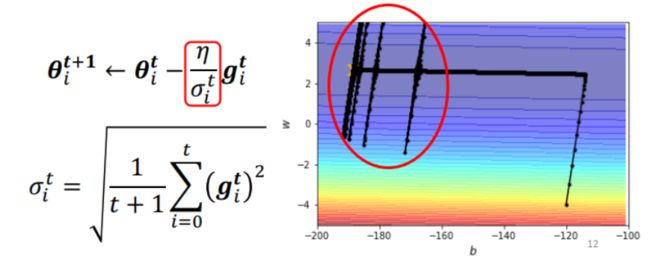
不一定。可能此时 gradient 并不小。如下图中红色圆圈所示，loss 不再下降，然而 gradient 却一直在波动。

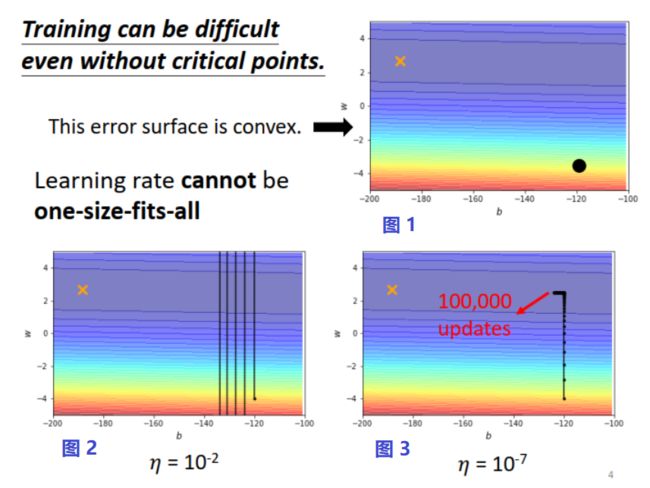
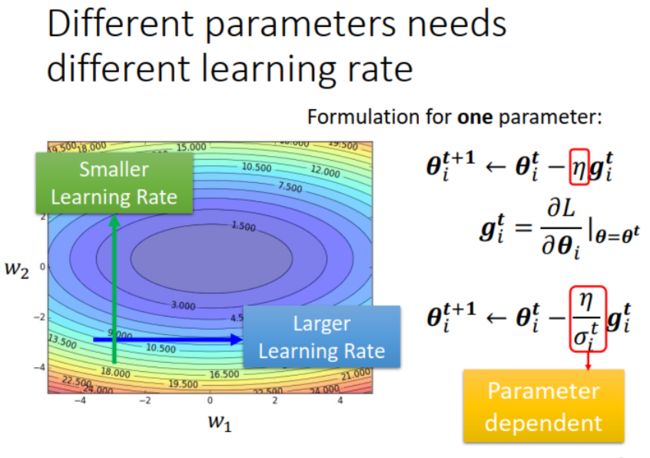
是什么原因？来看一个具体的例子。下图所示为有两个参数模型的 convex error surface，是理想的 error surface，存在 loss 最小值（图中打叉点所示）。参数 $w$（纵轴）的 loss 曲线陡峭，而参数 $b$（横轴）的 loss 曲线平缓。假设参数优化的起始点在下图 1 中黑点所示位置，如果 learning rate 设大一些，纵轴方向调整时，在“山谷两侧陡峭的崖壁”来回震荡，如下图 2 所示；如果 learning rate 设小一些，横轴方向调整时，在“平缓的盆地”进展缓慢，如下图 3 所示。可见一个 learning rate 难以满足不同参数的调整步子 ( step ) 要求。

解决办法：引入 ${\sigma }_i^t$ ，与参数 $i$ 和更新次数 $t$ 都有关，让不同的参数有不同的 learning rate。

（1）Adagrad

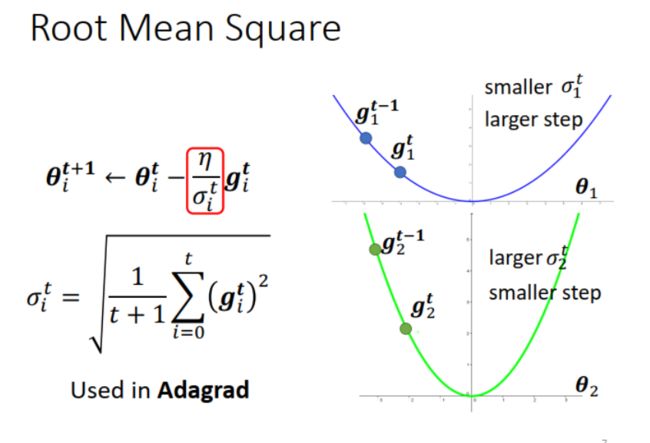
Adagrad：${\sigma }_i^t$ 取本次和以前的 gradients 的 Root Mean square。如下图所示，某个参数 ${\theta }_1$的 gradient 小，loss 曲线平缓，那么 ${\sigma }_1^t$ 小，step 大；反之，某个参数 ${\theta }_2$ 的 gradient 大，loss 曲线陡峭，那么 ${\sigma }_2^t$ 大，step 小。

疑问：${\sigma }_i^t$ 如果与参数有关的话，${\sigma }^t$ 是个标量还是矢量？如果是标量，那么是计算各参数的 ${\sigma }_i^t$ 之和？

我在李沐老师的《动手学深度学习》AdaGrad一节 找到了答案，不同的参数，通过计算其 $g_i^t$ 得到对应的 ${\sigma }_i^t$。例如，对于 loss function 为 $f(x)=0.1x_1^2+2x_2^2$ ，书中的示例代码为：

def adagrad_2d(x1, x2, s1, s2):
    g1, g2, eps = 0.2 * x1, 4 * x2, 1e-6  # 前两项为自变量梯度
    s1 += g1 ** 2
    s2 += g2 ** 2
    x1 -= eta / math.sqrt(s1 + eps) * g1
    x2 -= eta / math.sqrt(s2 + eps) * g2
    return x1, x2, s1, s2

可以看到，代码中的 $s_1$ 和 $s_2$ 分别是 g1 的平方累积和 g2 的平方累积，而 ${\sigma }_1^t$ 和 ${\sigma }_2^t$ 分别对应代码中的$\sqrt{s1}$ 和 $\sqrt{s2}$。也就是说，不同的参数有不同的 ${\sigma }_i^t$，因此有不同的 learning rate。同时也注意到，g 的取值是有正有负，标识了变化方向。而 ${\sigma }_1^t$ 取值均为非负值，标识大小。

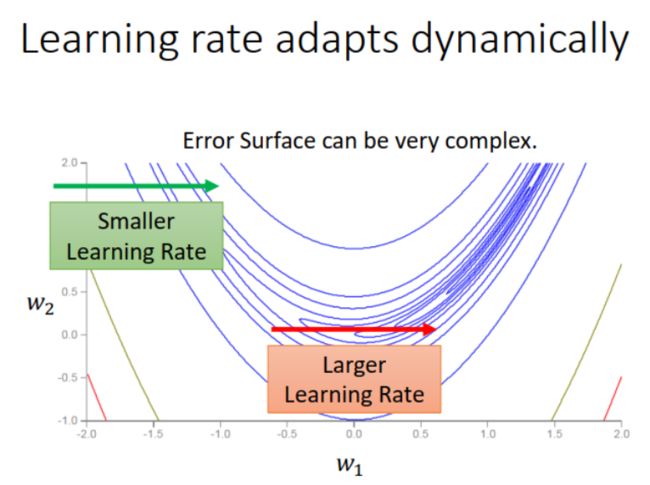
Adagrad 存在的问题：${\sigma }_i^t$ 是 gradient 的累积平均，对 gradient 的变化反应不够快。如下图中的参数 $w_1$，绿色箭头处 loss 曲线陡峭，gradient 大，需要 smaller step；而到了红色箭头处 loss 曲线平缓，gradient 小，要 larger step。怎么才能更快地应对 gradient 变化呢？

解决办法：引入 weight，加大本次 gradient 的权重。这就是 RMSProp。

（2）RMSProp

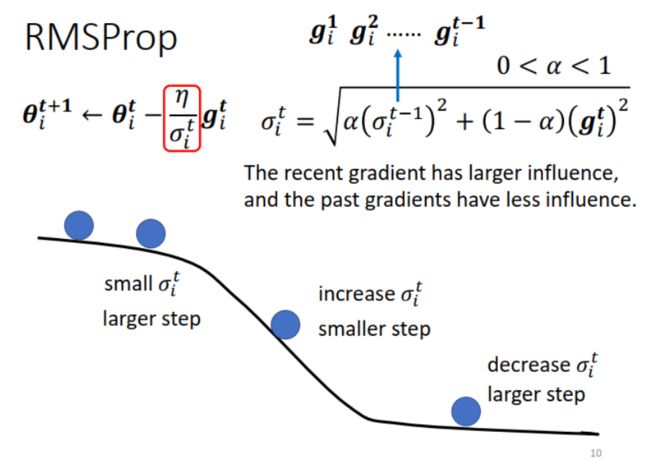
RMSProp: ${\sigma }_i^t$ 取本次和以前 gradients 的 weighted Root Mean Square。通过调整 $\alpha$ ，可以决定当前 gradient 的影响力，从而对 gradient 的变化反应更快。例如遇到下图所示的 loss 曲线先平缓、再陡峭、又平缓的情况，如果用 Adagrad，因为计算的是本次和历史 gradients 的平均，反应慢，很容易在中间陡峭段因为 step 大“飞出去”。而用 RMSProp，可以给 $\alpha$ 设置一个较小的值，从而使当前 gradient 的作用大，在陡峭段 ${\sigma }_i^t$ 会快速变大，从而调小 step。到了下一个平缓段，${\sigma }_i^t$ 又会快速变小，从而调大 step。

（3）Adam

Adam：RMSProp+Momentum

疑问：分子分母都是计算的累积 gradients，会不会抵消呢？

不会。momentum 是向量，既有大小、又有方向。RMSProp 是标量，只是计算大小。

（4）Learning Rate Scheduling

前面例子的两参数模型，应用 Adagrad 之后，优化过程如下图所示，接近终点处为什么会在纵轴来回摆动呢？

原因：此时，纵轴方向 ($w$) 的 gradient 很小，经过一段时间累积平均，${\sigma }_w^t$ 变得很小，于是 step 变大，$w$ 这一步的变化就“飞出来”了，到纵轴方向 gradient 大的地方。同时由于 step 大，和前面介绍的 learning rate 大的情况一样，在“山谷两侧的崖壁”来回震荡。但是，过一段时间，${\sigma }_w^t$ 也会逐渐变大，因此 step 变小， $w$ 又会变化调整回到中心。

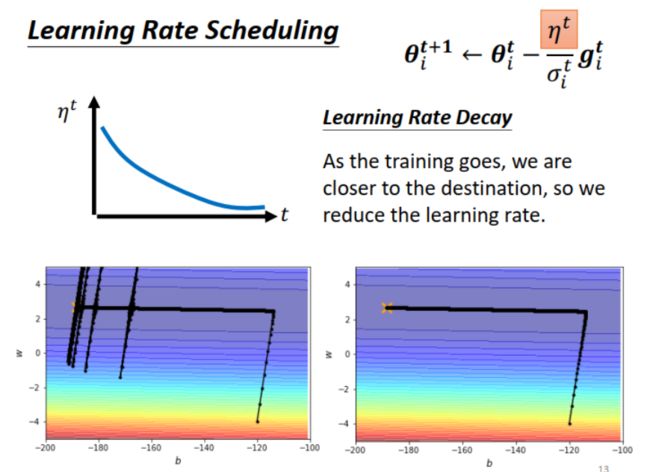
看来，应该让 learning rate 本身也变化，开始大一点，到训练后期（接近 loss 低值），就要小。这就是 Learning Rate Scheduling，如下图所示。应用这一方法后， $w$ 的变化就不会“飞出”，而是顺利到达最优点。

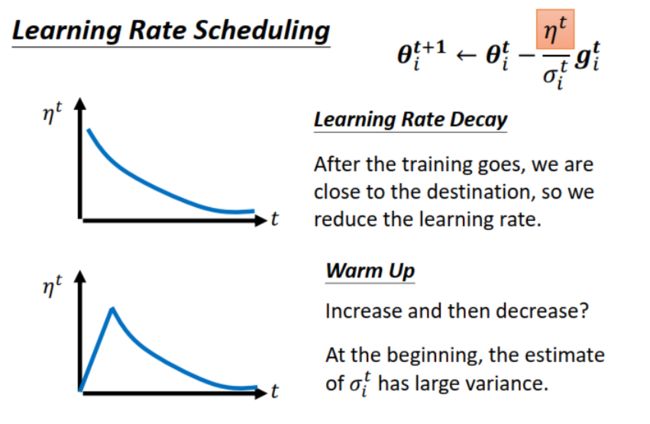
有两种 Learning Rate Scheduling:

learning rate decay：learning rate 的变化： 大–>小

warm up：learning rate 的变化：小–>大–>小。这个名字取得很有意思，好像 learning rate 也要热身，哈哈。warm up 是许多知名模型（例如 ResNet，Transformer）都会使用的一个训练技巧。为什么初始 learning rate 先不设大？一个解释是 ${\sigma }_i^t$ 是历史 gradients 的统计值，一开始时计算的次数少，可能并不准确，所以一开始步子不宜迈大，先小步探索。

结合 2 和 3，综合应用 momentum 和 adaptive learning rate:

4. 改变 error surface

从分类问题说起：

如何做分类 ( classification ) ?

首先想到的方法是把类别用数字表示，例如，输出按类别表示为 1，2，3，……，这样转化为一个回归问题 ( regression ) 。

但是这样做有一个问题：不同类别并不一定有大小、顺序关系，比如颜色红、黄、蓝，如果按数字来定类别，就人为设置了相邻的两个类别更接近，这不符合事实，容易造成误判。

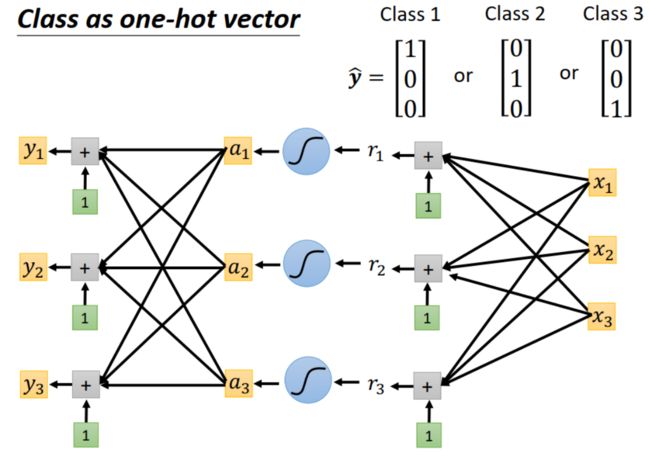
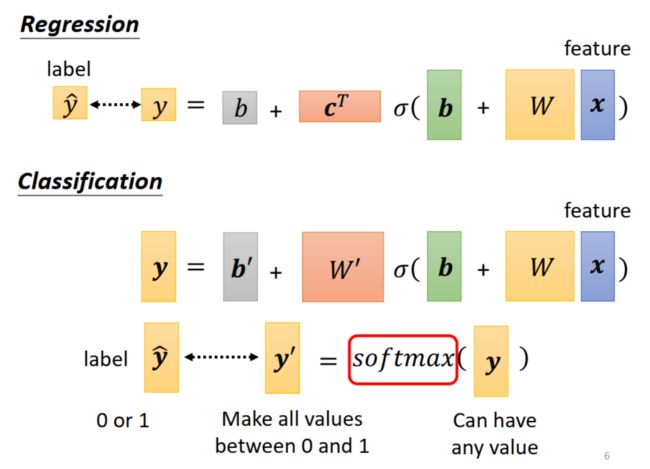
解决办法：使用 one-hot vector，如下图右上角所示，对应类别处值为 1 ，其余地方值为 0。这样，原来 1 个输出变成多个输出。在神经网络中的实现也简单，如下图所示，在输出部分增加几个线性单元即可。

进一步地，因为 one-hot vector 的值都是 0 或者 1，用 softmax 把输出值限制到 [0,1] 之间，好和 one-hot vector 计算相似度。

对于两分类问题，用 sigmoid 与 softmax 等效。

loss function 还是和 regression 一样，用 MSE 吗？

不是，用 cross entropy 比 MSE 更好。why?

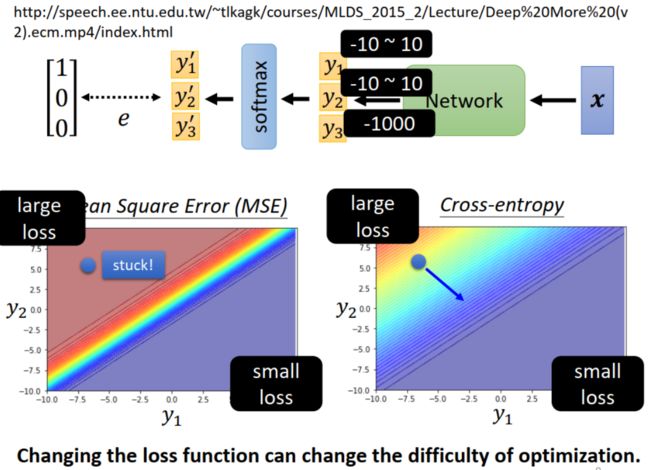
原因：error surface。用一个直观例子解释，假设有一个三分类的模型，其中 $y_1$ 和 $y_2$ 这两类起主要作用，由 $y_1$ 和 $y_2$ 绘制（是参数吗？）的 error surface 如下图所示。可以看到，不论用 MSE 还是 Cross Entropy，都是左上角区域 loss 大，右下角区域 loss 小，假设训练开始时位于图中左上角蓝色点所示位置。如果 loss function 用 MSE，因为这一区域 loss 变化平缓，训练容易卡住。如果 loss function 用 Cross Entropy，因为这一区域 loss 变化陡峭，可以变化到 loss 更低的点。

这也就是说，改变 loss function，可以改变 error surface（平缓或是陡峭），因此改变训练的难易程度。

听课收获

学到了很多 optimization 方面的知识，包括一些具体情况的处理，例如：模型的 loss 大，应该从哪里找原因？ loss 不下降，训练卡住时，应该怎么办？做作业时看到老师的示例代码里设置了 batch size，用了 Adam 作为 optimizer，设置了 momentum 参数等，当时对这些都不太懂，学习了这节课之后明白了其中的原理。

本文对您有帮助的话，请点赞支持一下吧，谢谢！

关注我 宁萌Julie，互相学习，多多交流呀！

阅读更多笔记，请点击 李宏毅老师《机器学习》笔记–合辑目录。

参考

1.李宏毅老师《机器学习 2022》，

课程网站：https://speech.ee.ntu.edu.tw/~hylee/ml/2022-spring.php

视频：https://www.bilibili.com/video/BV1Wv411h7kN

2.《动手学深度学习》，AdaGrad 算法：http://zh.gluon.ai/chapter_optimization/adagrad.html