Multi-hop Reading Comprehension through Question Decomposition and Rescoring 论文笔记

Multi-hop Reading Comprehension through Question Decomposition and Rescoring

2019年的一篇在Hotpot数据集上进行实验的文章，由UW和AllenAI共同发表。

Overview

这篇文章是在HotpotQA数据集提出后发表的，针对HotpotQA所提出的复杂问题多跳推理任务提出解决方案。本文所提出的模型叫做DECOMPRC，核心在于DECOMP，也就是对复杂问题进行分解。这种做法在KBQA中也出现过，对应的模型叫做TextRay。对于分解问题的做法，我认为有三个核心点：

1. 如何从原复杂问题中获得简单问题，也就是子问题提取任务
2. 如何对子问题答案进行合并来得到原问题的答案，也就是子问题答案的合并策略
3. 子问题的答案如何获取

对于第一点，这篇文章所采取的做法是通过span prediction来生成子问题，并且，作者把对子问题的推理分了四类；对于第二点，作者首先使用单跳的问答模型对子问题进行回答，然后设计了一个打分器来判断哪种分解是最优的，并得出最终的答案。对于第三点，本文的做法是人工标注了400条数据并且发现即使只有400条，模型训练出的效果也很不错。

Model

本文的模型主要分为三个部分：

1. Decomposition：这一部分就是用来对原问题进行分解的
2. Single-hop Reading Comprehension：训练一个单跳问答模型来回答所有的子问题
3. Decomposition Scorer：训练一个打分器来判断哪种分解方式是最优的

Decomposition

复杂问题简单化是一个容易想到的思路，因此本文采取了这种策略。KBQA任务下的TextRay模型也尝试对复杂问题进行单跳分解，不过它是基于query graph来做的，它的合并策略是设计两种操作：join和simQA，其实表示了分解出的简单问题之间的两种关系：并列和递进。递进的意思是说问题A答案是回答问题B的关键信息之一。

本文也是通过对问题进行分析，得到了几个简单问题构成一个复杂问题的四种类型：Bridging、Intersection、Composition、Original。下面用下图的这个问题为例来解释四种推理类型分别是什么意思

1. Bridging：这种类型就和前面说的递进关系是一样的，前一个问题的答案需要被用来回答下一个问题

2. Intersection：这个和并列关系比较像，原问题的答案是子问题A答案和子问题B答案的交集

3. Comparison：这个类型是专门应对HotpotQA中比较难回答的比较类问题，提取出比较的操作（比如larger、younger），然后得到所有子问题的答案，最终的答案根据在所有子问题答案上执行操作来得到

4. Original：这一类就是直接用原问题进行回答，可能是考虑到HotpotQA中easy的部分全都是单跳推理问题

Span Prediction for Sub-Question Generation

本文的子问题获取感觉是一个创新点，是通过span prediction来得到的。具体做法如下：

首先作者用BERT对原问题$S=\{s_1,s_2,\dots ,s_n\}$做一层编码得到
$$U=BERT(S)\in R^{n\times h}$$
然后，预测span的方法是训练一个$Pointe{r}_c$，这里的$c$表示的是一个数量，$c$个pointer分别指向$c$个index，记为$in{d}_1,in{d}_2,\dots ,in{d}_c$，会把原问题分成$c+1$段。接下来，再对编码后的问题向量做一个线性映射，映射到$R^c$空间，然后再接一个softmax
$$Y=softmax(UW)\in R^{n\times c}$$
不难看出，$Y_{ij}$表示的就是原问题中第$i$个token属于$in{d}_j$的概率。

上图展示了如何利用这个Pointer来对Bridging、Intersection、Comparison三类问题进行分解。Bridging用到了3个pointer，Intersection用到了2个pointer，Comparison用到了4个pointer。Intersection和Comparison的分解看伪代码还是比较清楚的，但这里Bridging的分解看的不是特别明白。

Single-hop Reading Comprehension

对于单跳的问答模型，作者直接使用的BERT，并且在SQuAD和HotpotQA easy上进行训练。由于HotpotQA涉及到multi-paragraph，因此作者采用了《Simple
and effective multi-paragraph reading comprehension》这篇文章的段落选取方法。HotpotQA + SQuAD的训练上作者设计了一个多任务学习，不仅要预测答案的span，还要判断是否有答案（针对SQuAD），并且判断是否为supporting fact（针对HotpotQA）。做法上很简单，用BERT编码然后直接线性映射，再套softmax。

Decomposition Scorer

对于分解方案的打分，本文的做法如下：

令$t$表示reasoning type，$answe{r}_t$、$evidenc{e}_t$分别表示对应的答案和依据。令$x$表示这三者文本加原问题文本的concatenation，也就是$x_t=[t;answe{r}_t;evidenc{e}_t;question]$。然后作者再用一个BERT对每种类别的$x_t$进行编码，然后做线性映射，由于现在是一个二分类任务，因此再套一个sigmoid
$$scor{e}_t=sigmoid(W_2^T\max (U_t))$$
$W_2\in R^h$，$max(U_t)$是在$n$维度上取最大值。最终，最优的type为
$$t^{\ast }=argma{x}_t(scor{e}_t)$$
这里的做法是decompose后预测reason type，作者还提出了另一种做法，在decompose之前就预测最优的reason type，不过做法上没区别，只是输入会变成只有问题的编码。

Experiment

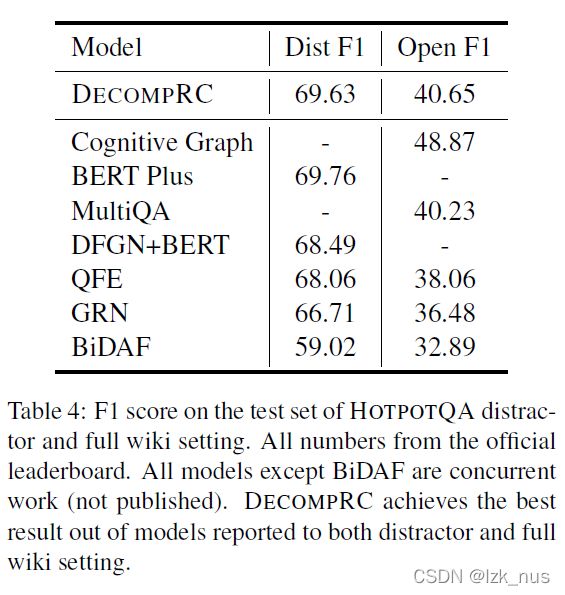
先看在HotpotQA数据集上的表现

对于单跳推理模型，作者使用BiDAF、BERT作为baseline进行对比

作者还用人工生成子问题与本文的span prediction方法效果进行了对比，发现span prediction的方法比人工差不了太多

接下来，作者还做了一些工作来测试鲁棒性，具体有两个：

1. 对distractor部分的noise段落进行修改来测试模型鲁棒性，发现F1仅下降了3.41；
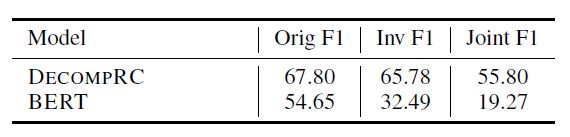
2. 针对比较类问题，作者使用了相反的问题进行测试，比如说原来问which is younger，现在改为which is older。

作者发现相较于BERT，DECOMPRC的鲁棒性要好很多