深度学习笔记之正则化、激活函数、卷积

一. 正则化(Regularization)

正则化是一类通过限制模型复杂度，从而避免过拟合，提高泛化能力的方法。

1. $L_1$、$L_2$正则化

在没有添加正则化项前，我们的损失函数是：$J(\theta ;x,y)$。
而添加正则化后，相当于对损失函数引入了惩罚（约束条件），损失函数变为：$\hat{J}(\theta ;x,y)=J(\theta ;x,y)+\beta \Omega (\theta )$。
其中：

• $\theta$为训练参数;
• $x$是输入;
• $y$是输出;
• $\beta$是超参数,对范数惩罚的贡献进行加权，从而影响正则化的效果;

$L_2$正则化：

$L_2$正则化又称为岭回归或者权重衰减，其表达式为：$\Omega (\theta )=\frac{1}{2}||w|{|}_2^2$，引入$L_2$正则化后，我们的损失函数变为：
$$\hat{J}(\theta ;x,y)=J(\theta ;x,y)+\frac{\beta }{2}||w|{|}_2^2$$
损失函数的梯度计算为：
$${▽}_w\hat{J}={▽}_{w}J+\beta w$$
对于$w$的更新则为：
$$w=(1-\alpha \beta )w-\alpha {▽}_{w}J$$
其中$\alpha$为学习率，是超参数。

$L_1$正则化：

$L_2$正则化表达式为：$\Omega (\theta )=||w|{|}_1$，引入$L_2$正则化后，我们的损失函数变为：
$$\hat{J}(\theta ;x,y)=J(\theta ;x,y)+\beta ||w|{|}_1$$
$L_1$正则化与$L_2$正则化：

• 对比：$L_1$ 正则化会强制更多权重为零，而$L_2$则是降低所有权重的平均大小。换句话说，$L_1$ 建议应该从训练过程中丢弃一些特征。
• 结合使用：$\Omega (\theta )={\lambda }_1||w|{|}_1+{\lambda }_2||w|{|}_2^2$

2. Dropout

dropout相当于是向模型注入噪声，不过这种噪声是注入到网络的隐藏层单元。
dropout是指在训练期间，一定数量的层输出会被随机丢弃。而在测试阶段，所有的单元都存在。

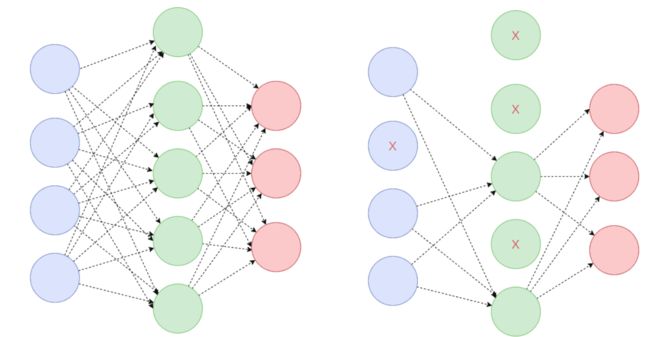
通过引入dropout增加了网络的稀疏性。
dropout有效地原因：

• 节点对其他节点的权重变得更加不敏感，因此模型更加健壮。如果一个隐藏单元必须与其他隐藏单元的不同组合一起工作，那么它更有可能做一些单独有用的事情。
• Dropout 可以看作是对多个模型（“集成”）进行平均的一种形式。

3. 数据增强

数据增强指为我们的数据集生成新的训练示例的过程。更多的训练数据意味着更低的模型方差，也就是更低的泛化误差。
数据增强的方法：图像翻转、裁剪、旋转、平移、图像颜色修改、图像混合等

4. 提前停止

提前停止指当训练误差不再减小但验证误差开始上升时停止训练的过程。

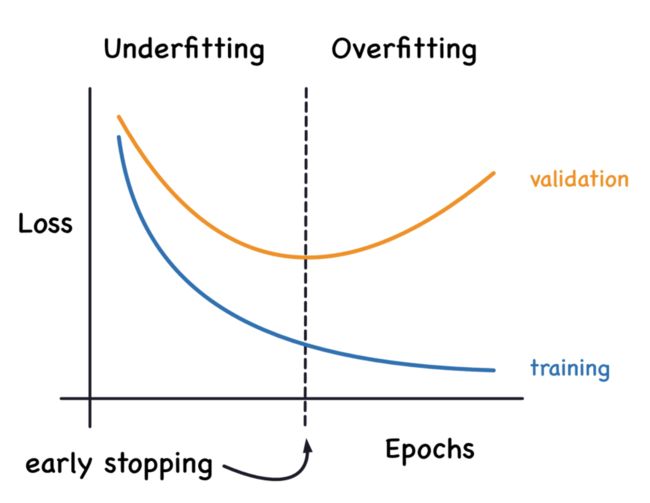
5. 批标准化

本质上是注入噪声。它不是将每个隐藏单元与一个随机值相乘，而是将它们与小批量中所有隐藏单元的偏差相乘。它还在每一步从每个隐藏单元中减去一个随机值（小批量的平均值）。这两种“噪音”都会使模型更加健壮并减少其方差

二. 激活函数

引入激活函数的主要原因是让原本线性的模型变为非线性，使得模型能够处理线性不可分的问题，如异或问题。
由于之前已经写过常见的激活函数（relu，tanh，sigmoid），这篇文章就说点新的补充内容。

1. 激活函数需要具备的性质

• 连续并可导（允许少数点上不可导）的非线性函数。
• 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。
• 激活函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。

2. 死亡Relu问题

什么是死亡Relu：
在训练过程中，如果参数在一次不恰当的更新后，第一个隐藏层中的某个Relu神经元在所有的训练数据上都不能被激活，那么这个神经元自身参数的梯度永远都会是0，以后的训练过程中永远不能被激活。

避免死亡Relu的方法：

• 使用带泄露的Relu(Leaky Relu)，带参数的Relu（Parametric Relu）等。

$$\begin{array}{rlr}Rel{u}_{leaky}=\{\begin{array}{ll}x& x>0\\ \lambda x& x\le 0\end{array}& & Rel{u}_{parametic}=\{\begin{array}{ll}x& x>0\\ \alpha x& x\le 0\end{array}\end{array}$$

• 使用较小的学习率：较大的学习率导致负权重的可能性更高（从而增加了 ReLU 死亡的机会），因此在训练过程中降低学习率。

三. 卷积

1. 池化（pooling）

作用：进行特征选择，降低特征的数量，从而减少参数数量。

卷积与池化：卷积减少连接的数量，池化减少参数的数量。

1×1卷积：1x1卷积实际上是对每个像素点，在不同的channels上进行线性组合且保留了图片的原有平面结构，调控depth，从而完成升维或降维的功能。

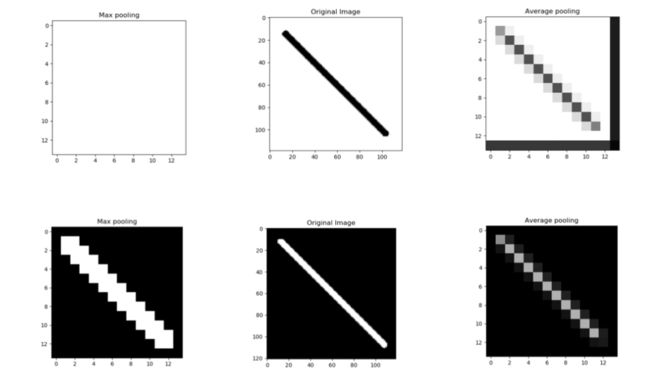
最大池化（max pooling）与平均池化(average pooling)

• 最大池化仅提取数据最显着的特征；平均池化平滑提取特征。
• 平均池化有时无法提取重要特征，因为它考虑了所有因素，并给出了可能重要或不重要的平均值；最大池化只关注非常重要的特征。
• 平均池化鼓励网络识别对象的完整范围；最大池化将其限制为仅非常重要的特征，并且可能会遗漏一些细节。
  -

2.转置卷积

卷积操作实现了高维特征向低维特征的转换，而转置卷积则实现了将低维特征映射到高维特征。
具体来说，假设$x$是一个高维张量，$z$是一个低维张量，那么可以用仿射变换来实现高维到低维的映射。
$$z=Wx$$
而我们很容易地通过转置$W$来实现低维到高维的映射。
$$x=W^{T}z$$
卷积操作可以写成仿射变化的形式，例如：
$$\begin{array}{rl}z& =w\otimes x\\ & =\left[\begin{array}{ccccc}{w}_1& w_2& w_3& 0& 0\\ 0& w_1& w_2& w_3& 0\\ 0& 0& w_1& w_2& w_3\end{array}\right]x\\ & =Cx\end{array}$$
其中:

• $w=[w_1,w_2,w_3{]}^T$
• $\otimes$表示卷积操作

那么转置卷积就有：

$$\begin{array}{rl}z& =C^{T}x\\ & =\left[\begin{array}{ccc}{w}_1& 0& 0\\ w_2& w_1& 0\\ w_3& w_2& w_1\\ 0& w_3& w_2\\ 0& 0& w_3\end{array}\right]x\\ & =rot180(w)\hat{\otimes }x\end{array}$$
转置卷积的示意图：

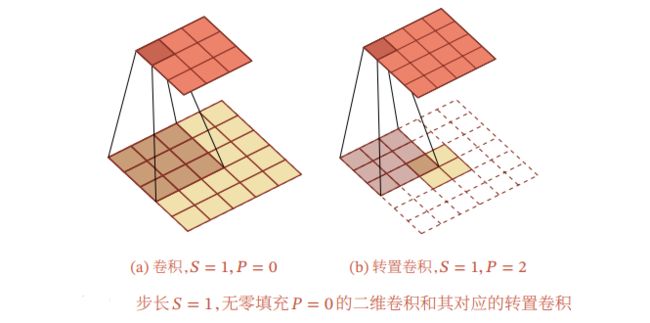
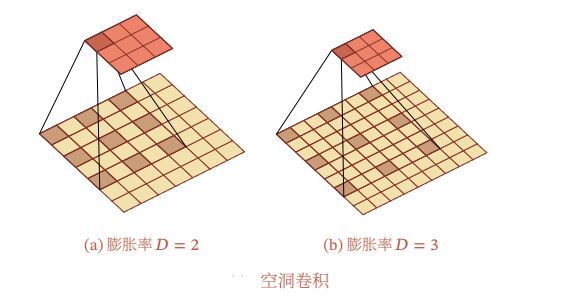
3.空洞卷积

定义：
空洞卷积是一种不增加参数数量，同时增加输出单元感受野的一种方法，也称为膨胀卷积。

实现：
空洞卷积通过给卷积核插入“空洞”来变相地增加其大小。如果在卷积核的每两个元素之间插入$D-1$个空洞，则卷积核的有效大小为：
$$\hat{K}=K+(K-1)\times (D-1)$$
其中$D$称为膨胀率，当$D=1$时卷积核为普通卷积核。

参考

• Regularization techniques for training deep neural networks
• 神经网络与深度学习