C++元编程——四维矩阵简单运算实现
基于原来的矩阵,进行了魔改,形成了四维矩阵的点积运算,效果拔群,对于矩阵的运算有效。老规矩,先上测试代码:
#include "mat.hpp"
int main(int argc, char** argv)
{
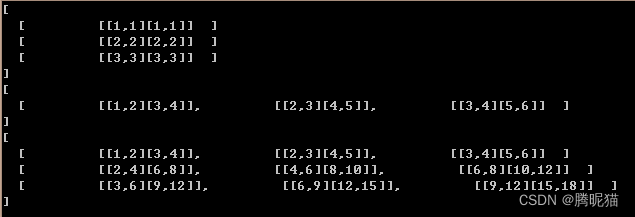
mat<3, 1, mat<2, 2, double > > m3d{1,2,3};
m3d.print();
mat<1, 3, mat<2, 2, double> > m3d2{ {1,2,3,4},{2,3,4,5},{3,4,5,6} };
m3d2.print();
auto k = m3d.dot(m3d2);
k.print();
return 0;
}四维矩阵是一个二维矩阵,其每个元素都是一个二维矩阵。点积运算规则和二维一致,只是每个元素的运算换做了矩阵对应元素的对乘,对加,仅此而已。但是这却完全体现出了C++元编程的牛X之处。如果是运行时,你就要重新定义一个类型,然后定义这个类型的加减乘除。但是元编程不用,如果推导合理,但是你必须把普通标量运算实现出矩阵版本。运行结果如下:
结果也是NICE的,正确算出了这两个四维矩阵的点积。下面是修改的代码。
base_function.hpp对原来的点积运算参数推导进行了细化:
#ifndef _BASE_FUNCTION_HPP_
#define _BASE_FUNCTION_HPP_
#include "base_logic.hpp"
template
auto derivative(func_t&& f, const decltype(f(0))& v)
{
constexpr double SMALL_VAL = 1e-11;
return (f(v + SMALL_VAL) - f(v - SMALL_VAL)) / (2. * SMALL_VAL);
}
/* 点乘运算 */
template
inline vt n_dot(const mat& mt1, const mat& mt2)
{
static_assert(c1 == r2, "[matrix dot error]\tleft matrix column number do not match right matrix's row number.");
if constexpr (c1 != 0 || r2 != 0)
{
return mt1.get_val() * mt2.get_val() + n_dot(mt1, mt2);
}
if constexpr (c1 == 0 && r2 == 0)
{
return mt1.get_val() * mt2.get_val();
}
}
template
class v_dot
{
public:
template
static vt cal(const mat& mt1, const mat& mt2)
{
return n_dot(mt1, mt2);
}
};
template
mat dot(const mat& mt1, const mat& mt2)
{
using omatt = mat;
using imatt1 = mat;
using imatt2 = mat;
omatt mt_ret;
col_loop(mt_ret, mt1, mt2);
return mt_ret;
}
/* 加法运算 */
template
class v_add
{
public:
template
static vt cal(const imatt1& mt1, const imatt2& mt2)
{
return mt1.get_val() + mt2.get_val();
}
};
template
class n_add
{
public:
template
static vt cal(const vt& mt1, const imatt2& mt2)
{
return mt1 + mt2.get_val();
}
};
template
struct c_add
{
template
static vt cal(const mat& mt, const mat& v)
{
return mt.get_val() + v.get_val();
}
};
template
struct r_add
{
template
static vt cal(const mat& mt, const mat<1, col_num, vt>& v)
{
return mt.get_val() + v.get_val<0, c>();
}
};
template
mat operator+(const mat& mt1, const mat& mt2)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, mt1, mt2);
return mt_ret;
}
template
mat operator+(const val_t& v, const mat& mt)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, v, mt);
return mt_ret;
}
template
mat operator+(const mat& mt, const val_t& v)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, v, mt);
return mt_ret;
}
template
mat operator+(const mat& mt, const val_t_other& v)
{
return mt + static_cast(v);
}
template
mat operator+(const val_t_other& v, const mat& mt)
{
return mt + static_cast(v);
}
template
void spread_add(mat& mt_ret, const mat& mt, const mat& v)
{
col_loop(mt_ret, mt, v);
}
template
void spread_add(mat& mt_ret, const mat& mt, const mat<1, col_num, val_t>& v)
{
col_loop(mt_ret, mt, v);
}
template
void spread_add(mat& mt_ret, const mat& mt, const mat<1, 1, val_t>& v)
{
col_loop(mt_ret, v.get_val<0, 0>(), mt);
}
template
void spread_add(mat& mt_ret, const mat& v, const mat& mt)
{
col_loop(mt_ret, mt, v);
}
template
void spread_add(mat& mt_ret, const mat<1, col_num, val_t>& v, const mat& mt)
{
col_loop(mt_ret, mt, v);
}
template
void spread_add(mat& mt_ret, const mat<1, 1, val_t>& v, const mat& mt)
{
col_loop(mt_ret, v.get_val<0, 0>(), mt);
}
template
void spread_add(mat<1, 1, val_t>& mt_ret, const mat<1, 1, val_t>& v, const mat<1, 1, val_t>& mt)
{
col_loop<0, n_add>(mt_ret, v.get_val<0, 0>(), mt.get_val<0, 0>);
}
/* 减法运算 */
template
class v_minus
{
public:
template
static vt cal(const imatt1& mt1, const imatt2& mt2)
{
return mt1.get_val() - mt2.get_val();
}
};
template
class n_minus
{
public:
template
static vt cal(const vt& v, const mat& mt2)
{
return v - mt2.get_val();
}
template
static vt cal(const mat& mt2, const vt& v)
{
return mt2.get_val() - v;
}
};
template
mat operator-(const mat& mt1, const mat& mt2)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, mt1, mt2);
return mt_ret;
}
template
mat operator-(const val_t& v, const mat& mt)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, v, mt);
return mt_ret;
}
template
mat operator-(const mat& mt, const val_t& v)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, mt, v);
return mt_ret;
}
template
mat operator-(const mat& mt, const val_t_other& v)
{
return mt - static_cast(v);
}
template
mat operator-(const val_t_other& v, const mat& mt)
{
return (static_cast(v) - mt);
}
/* 乘法运算 */
template
class n_mul
{
public:
template
static vt cal(const vt& mt1, const imatt2& mt2)
{
return mt1 * mt2.get_val();
}
};
template
class v_mul
{
public:
template
static vt cal(const imatt1& mt1, const imatt2& mt2)
{
return mt1.get_val() * mt2.get_val();
}
};
template
mat operator*(const val_t& v, const mat& mt)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, v, mt);
return mt_ret;
}
template
mat operator*(const mat& mt, const val_t& v)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, v, mt);
return mt_ret;
}
template
mat operator*(const mat& mt1, const mat& mt2)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, mt1, mt2);
return mt_ret;
}
/* 除法 */
template
class n_div
{
public:
template
static vt cal(const mat& mt, const vt& v)
{
return mt.get_val() / v;
}
template
static vt cal(const vt& v, const mat& mt)
{
return v / mt.get_val();
}
};
template
class v_div
{
public:
template
static vt cal(const mat& mt1, const mat& mt2)
{
return mt1.get_val() / mt2.get_val();
}
};
template
mat operator/(const mat& mt, const val_t& v)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, mt, v);
return mt_ret;
}
template
mat operator/(const val_t& v, const mat& mt)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, v, mt);
return mt_ret;
}
template
mat operator/(const mat& mt1, const mat& mt2)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, mt1, mt2);
return mt_ret;
}
template
class n_sqrt
{
public:
template
static vt cal(const imatt& mt)
{
return sqrtl(mt.get_val());
}
};
template
mat sqrtm(const mat& mt)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, mt);
return mt_ret;
}
/* exp运算 */
template
struct n_exp
{
template
static typename imatt::type cal(const imatt& mt)
{
return exp(mt.get_val());
}
};
template
mat expm(const mat& mt)
{
using omatt = mat;
omatt mt_ret;
col_loop(mt_ret, mt);
return mt_ret;
}
/* 卷积运算 */
template
inline auto col_loop_mul(const imat_origin& mt_origin, const imat_tpl& mt_tpl)
{
if constexpr (col_delta != 0)
{
return mt_origin.get_val() * mt_tpl.get_val()
+ col_loop_mul(mt_origin, mt_tpl);
}
if constexpr (col_delta == 0)
{
return mt_origin.get_val() * mt_tpl.get_val();
}
}
template
inline auto row_loop_add(const imat_origin& mt_origin, const imat_tpl& mt_tpl)
{
if constexpr (row_delta != 0)
{
return col_loop_mul(mt_origin, mt_tpl)
+ col_loop_mul(mt_origin, mt_tpl);
}
if constexpr (row_delta == 0)
{
return col_loop_mul(mt_origin, mt_tpl);
}
}
template
struct v_inner_conv
{
template
inline static auto cal(const imat_origin_t& mt_origin, const imat_tpl_t& mt_tpl)
{
return row_loop_add(mt_origin, mt_tpl);
}
};
constexpr int get_step_inner_size(int i_origin, int i_tpl, int i_step)
{
return (i_origin - i_tpl) / i_step + 1;
}
constexpr int get_pad_size(int i_origin, int i_tpl, int i_step)
{
return (((i_origin - i_tpl) / i_step) + (((i_origin - i_tpl) % i_step) == 0 ? 0 : 1)) * i_step - (i_origin - i_tpl);
}
constexpr int get_ceil_div(int i_origin, int i_tpl)
{
return (i_origin / i_tpl + ((i_origin % i_tpl) == 0 ? 0 : 1));
}
template
struct pad_size_t
{
static constexpr int top = get_pad_size(input_row, tpl_row, row_step) / 2;
static constexpr int left = get_pad_size(intput_col, tpl_col, col_step) / 2;
static constexpr int right = get_pad_size(intput_col, tpl_col, col_step) - left;
static constexpr int bottom = get_pad_size(input_row, tpl_row, row_step) - top;
};
template
inline mat
inner_conv(const mat& mt_origin, const mat& mt_tpl)
{
using ret_type = mat;
ret_type mt_ret;
col_loop(mt_ret, mt_origin, mt_tpl);
return mt_ret;
}
template
struct st_one_col
{
static constexpr int all_size = (mat_t::r * mat_t::c) + st_one_col::all_size;
};
template
struct st_one_col
{
static constexpr int all_size = (mat_t::r * mat_t::c);
};
template
void concat_mat(typename mat_t::type* p, const mat_t& mt, const mat_ts... mts)
{
constexpr int cpy_size = mat_t::r * mat_t::c;
memcpy(p, mt.pval->p, cpy_size * sizeof(mat_t::type));
if constexpr (0 != sizeof...(mat_ts))
concat_mat(p + cpy_size, mts...);
}
template
mat::all_size, 1> stretch_one_col(const mat_t& mt, const mat_ts&...mts)
{
using ret_type = mat::all_size, 1>;
ret_type ret;
concat_mat(ret.pval->p, mt, mts...);
return ret;
}
template
void split_mat(typename mat_t::type* p, const mat_t& mt, const mat_ts... mts)
{
constexpr int cpy_size = mat_t::r * mat_t::c;
memcpy(mt.pval->p, p, cpy_size * sizeof(mat_t::type));
if constexpr (0 != sizeof...(mat_ts))
split_mat(p + cpy_size, mts...);
}
template
void split_one_mat(const mat_t& mt, const mat_ts&...mts)
{
split_mat(mt.pval->p, mts...);
}
#endif 矩阵类型定义mat.hpp,增加了输出函数的运算符,用来打印结果:
#ifndef _MAT_HPP_
#define _MAT_HPP_
#include
#include