深度学习知识点总结:优化器总结
深度学习知识点总结
专栏链接:
深度学习知识点总结_Mr.小梅的博客-CSDN博客本专栏主要总结深度学习中的知识点,从各大数据集比赛开始,介绍历年冠军算法;同时总结深度学习中重要的知识点,包括损失函数、优化器、各种经典算法、各种算法的优化策略Bag of Freebies (BoF)等。
本章介绍深度学习训练过程中用到的优化器。编辑中。。。
目录
2.4. 优化器
2.4.1. SGD
2.4.2. Adagrad
2.4.3. RMSprop
2.4.4. Adadelta
2.4.5. Adam
2.4.6. 学习率调度器
2.4. 优化器
2.4.1. SGD
SGD优化器计算过程
目标函数:y=2*x1+3*x2+4*x3
初始化:y=1*x1+2*x2+3*x3
损失函数:
l = (pred-gt)**2 = (wx1+wx2+wx3) ** 2
求导:
l`(w1) = 2(pred-gt)*x1
l`(w2) = 2(pred-gt)*x2
l`(w3) = 2(pred-gt)*x3
输入数据:
x = tensor([ 1.0943, 1.3479, -1.6927])
预测结果:
p = 1*1.0943+1*1.3479+1*-1.6927=0.7495
当weight_decay = 0
输出梯度:grad: tensor([[ 2.8188, 3.4719, -4.3600]])
手动计算验证:
l`(w1) = 2*(0.7495- -0.5384)*1.0943=2.81869794
l`(w2) = 2*(0.7495- -0.5384)*1.3479=3.47192082
l`(w3) = 2*(0.7495- -0.5384)*-1.6927=-4.36005666
权重更新:
w = tensor([[0.9718, 0.9653, 1.0436]], requires_grad=True)
w1:= 1-0.01*2.81869794=0.9718130206
w2:= 1-0.01*3.47192082=0.9652807918
w3:= 1-0.01*-4.36005666=1.0436005666
当weight_decay = 0.1
输出梯度:grad: tensor([[ 2.8188, 3.4719, -4.3600]])
手动计算验证:
===========
l`(w1) = 2*(0.7495- -0.5384)*1.0943=2.81869794
l`(w2) = 2*(0.7495- -0.5384)*1.3479=3.47192082
l`(w3) = 2*(0.7495- -0.5384)*-1.6927=-4.36005666
l`(w1) = l`(w1) + 0.1*1.0943=2.92812794
...
w=tensor([[0.9708, 0.9643, 1.0426]], requires_grad=True)
w1:= 1-0.01*2.92812794= 0.9707187206momentum即动量,它模拟的是物体运动时的惯性,即更新的时候在一定程度上保留之前更新的方向,同时利用当前batch的梯度微调最终的更新方向。这样一来,可以在一定程度上增加稳定性,从而学习地更快,并且还有一定摆脱局部最优的能力。
2.4.2. Adagrad
常见特征的参数相当迅速地收敛到最佳值,而对于不常见的特征,我们仍缺乏足够的观测以确定其最佳值。 换句话说,学习率要么对于常见特征而言降低太慢,要么对于不常见特征而言降低太快。
解决此问题的一个方法是记录我们看到特定特征的次数,然后将其用作调整学习率。在这里state_sum计下了我们截至时观察到功能的次数。 这其实很容易实施且不产生额外损耗。
特征的次数越多,state_sum值越大,学习率越小;特征的次数越少,state_sum值越小,学习率越大。
- AdaGrad算法会在单个坐标层面动态降低学习率。
- AdaGrad算法利用梯度的大小作为调整进度速率的手段:用较小的学习率来补偿带有较大梯度的坐标。
- 在深度学习问题中,由于内存和计算限制,计算准确的二阶导数通常是不可行的。梯度可以作为一个有效的代理。
- 如果优化问题的结构相当不均匀,AdaGrad算法可以帮助缓解扭曲。
- AdaGrad算法对于稀疏特征特别有效,在此情况下由于不常出现的问题,学习率需要更慢地降低。
- 在深度学习问题上,AdaGrad算法有时在降低学习率方面可能过于剧烈。
Adagrad计算过程如下
目标函数:y=2*x1+3*x2+4*x3
初始化:y=1*x1+2*x2+3*x3
损失函数:
l = (pred-gt)**2 = (wx1+wx2+wx3) ** 2
求导:
l`(w1) = 2(pred-gt)*x1
l`(w2) = 2(pred-gt)*x2
l`(w3) = 2(pred-gt)*x3
输入数据:
x = tensor([ 1.0943, 1.3479, -1.6927])
预测结果:
p = 1*1.0943+1*1.3479+1*-1.6927=0.7495
gt = tensor(-0.5384)
当weight_decay = 0
输出梯度:grad: tensor([[ 2.8188, 3.4719, -4.3600]])
手动验证过程:
l`(w1) = 2*(0.7495- -0.5384)*1.0943=2.81869794
l`(w2) = 2*(0.7495- -0.5384)*1.3479=3.47192082
l`(w3) = 2*(0.7495- -0.5384)*-1.6927=-4.36005666
statr_sum(w1) = 0 + l`(w1)**2
statr_sum(w2) = 0 + l`(w2)**2
statr_sum(w3) = 0 + l`(w3)**2
权重更新:
tensor([[0.9900, 0.9900, 1.0100]], requires_grad=True)
学习率:γ=0..1/(1+(1-1)*0)
w1:= 1-0.01*(l`(w1)/sqrt(statr_sum(w1)))=1-0.01=*0.99
w2:= 1-0.01*(l`(w1)/sqrt(statr_sum(w1)))=1-0.01=0.99
w3:= 1-0.01*(l`(w1)/sqrt(statr_sum(w1)))=1+0.01=1.01
第二轮输入x
x: tensor([ 0.3559, 0.2210, -1.1444])
pred: tensor([-0.5847], grad_fn=)
gt: tensor(-3.2028)
grad: tensor([[ 1.8634, 1.1574, -5.9923]])
weiht:tensor([[0.9845, 0.9868, 1.0181]], requires_grad=True)
手动验证过程:
l`(w1) = 2*(-0.5847--3.2028)*0.3559=1.86356358
l`(w2) = 2*(-0.5847--3.2028)*0.2210=1.1572002
l`(w3) = 2*(-0.5847--3.2028)*-1.1444=-5.99230728
statr_sum(w1) = 2.8188**2 + l`(w1)**2=11.418502656702417
statr_sum(w2) = 3.4719**2 + l`(w2)**2=13.393201912880041
statr_sum(w3) = (-4.3600)**2 + l`(w3)**2=54.917346537941
w1:= 1-0.01*(l`(w1)/sqrt(statr_sum(w1)))=0.99-0.01*(1.8634/sqrt(11.418502656702417))=0.9844855587710982
w2:= 1-0.01*(l`(w2)/sqrt(statr_sum(w2)))=0.99-0.01*(1.1572002/sqrt(13.393201912880041))=0.9868379677726956
w3:= 1-0.01*(l`(w3)/sqrt(statr_sum(w3)))=1.01-0.01*((-5.99230728)/sqrt(54.917346537941))= 1.0180861036311535 AdaGrad目标函数自变量中各个元素的学习率只能保持下降或者不变,因此当学习率在迭代早期降得较快且当前解依然不佳时,由于后期学习率过小,可能较难找到一个有用的解;
RMSProp和AdaDelta算法都是解决AdaGrad上述缺点的改进版本,本质思想都是利用最近的时间步的小批量随机梯度平方项的加权平均来降低学习率,从而使得学习率不是单调递减的(当最近梯度都较小的时候能够变大)。不同的是,RMSProp算法还是保留了传统的学习率超参数,可以显式指定。而AdaDelta算法没有显式的学习率超参数,而是通过Δx做运算来间接代替学习率;
Adam算法可以看成是RMSProp算法和动量法的结合。
2.4.3. RMSprop
Adagrad算法将梯度g的平方累加成状态矢量s(t)=s(t-1)+gt**2。 因此,由于缺乏规范化,没有约束力,s(t)持续增长,几乎上是在算法收敛时呈线性递增。
解决此问题的一种方法是使用s(t)/t,对于g的合理分布来说,它将收敛。 遗憾的是,限制行为生效可能需要很长时间,因为该流程记住了值的完整轨迹。 另一种方法是按动量法中的方式使用泄漏平均值,即s(t)=αs(t-1)+(1-α)*gt**2,其中参数α>0。 保持所有其它部分不变就产生了RMSProp算法。
- RMSProp算法与Adagrad算法非常相似,因为两者都使用梯度的平方来缩放系数。
- RMSProp算法与动量法都使用泄漏平均值。但是,RMSProp算法使用该技术来调整按系数顺序的预处理器。
- 在实验中,学习率需要由实验者调度。
- 系数α决定了在调整每坐标比例时历史记录的时长。
公式中的μb(t-1)的含义?
2.4.4. Adadelta
Adadelta是AdaGrad的另一种变体,主要区别在于前者减少了学习率适应坐标的数量。此外,广义上Adadelta被称为没有学习率,因为它使用变化量本身作为未来变化的校准。
v(t)用于存储梯度二阶导数的泄露平均值,Δx(t)用于存储模型本身中参数变化二阶导数的泄露平均值。
- Adadelta没有学习率参数。相反,它使用参数本身的变化率来调整学习率。
- Adadelta需要两个状态变量来存储梯度的二阶导数和参数的变化。
- Adadelta使用泄漏的平均值来保持对适当统计数据的运行估计。
2.4.5. Adam
SGD:随机梯度下降在解决优化问题时比梯度下降更有效
Mini batch SGD:在一个小批量中使用更大的观测值集,可以通过向量化提供额外效率。这是高效的多机、多GPU和整体并行处理的关键。
动量法:添加了一种机制,用于汇总过去梯度的历史以加速收敛。
Adagrad:通过对每个坐标缩放来实现高效计算的预处理器。
RMSProp:通过学习率的调整来分离每个坐标的缩放。
Adam算法 [Kingma & Ba, 2014]将所有这些技术汇总到一个高效的学习算法中。但是它并非没有问题,有时Adam算法可能由于方差控制不良而发散。 在完善工作中, [Zaheer et al., 2018]给Adam算法提供了一个称为Yogi的热补丁来解决这些问题。
2.4.6. 学习率调度器
-
多因子调度器
class FactorScheduler:
def __init__(self, factor=1, stop_factor_lr=1e-7, base_lr=0.1):
self.factor = factor
self.stop_factor_lr = stop_factor_lr
self.base_lr = base_lr
def __call__(self, num_update):
self.base_lr = max(self.stop_factor_lr, self.base_lr * self.factor)
return self.base_lr
scheduler = FactorScheduler(factor=0.9, stop_factor_lr=1e-2, base_lr=2.0)d2l.plot(torch.arange(50),
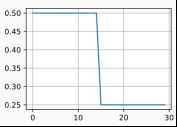
net = net_fn()trainer = torch.optim.SGD(net.parameters(), lr=0.5)scheduler = lr_scheduler.MultiStepLR(trainer, milestones=[15, 30], gamma=0.5)
-
余弦调度器
scheduler = CosineScheduler(max_update=20, base_lr=0.3, final_lr=0.01)- 其他
在某些情况下,初始化参数不足以得到良好的解。 这对于某些高级网络设计来说尤其棘手,可能导致不稳定的优化结果。 对此,一方面,我们可以选择一个足够小的学习率, 从而防止一开始发散,然而这样进展太缓慢。 另一方面,较高的学习率最初就会导致发散。
解决这种困境的一个相当简单的解决方法是使用预热期,在此期间学习率将增加至初始最大值,然后冷却直到优化过程结束。 为了简单起见,通常使用线性递增。 这引出了如下表所示的时间表。
scheduler = CosineScheduler(20, warmup_steps=5, base_lr=0.3, final_lr=0.01)- 在训练期间逐步降低学习率可以提高准确性,并且减少模型的过拟合。
- 在实验中,每当进展趋于稳定时就降低学习率,这是很有效的。从本质上说,这可以确保我们有效地收敛到一个适当的解,也只有这样才能通过降低学习率来减小参数的固有方差。
- 余弦调度器在某些计算机视觉问题中很受欢迎。
- 优化之前的预热期可以防止发散。
- 优化在深度学习中有多种用途。对于同样的训练误差而言,选择不同的优化算法和学习率调度,除了最大限度地减少训练时间,可以导致测试集上不同的泛化和过拟合量。