Q-learning\Sarsa解决12*12 grid world问题源码与总结
1 原理综述
Q-learning和Sarsa的原理已经有很多相关教程,详细内容推荐查看CS234强化学习课程第4-5讲。
总的来说,无论是Q-learning还是Sarsa,都是基于时序差分法控制的无模型策略迭代方法,属于Value-based强化学习算法大类中baseline的两种算法,因此两种算法很像。
相似点:
1、两种算法的本质都是为了通过策略迭代得到最优策略,而策略迭代又可以分为两个部分:策略评估和策略改进。
2、两种算法的控制策略都是基于时序差分法进行更新,与时序差分控制并列的还有蒙特卡洛仿真和动态规划,其中时序差分法可以看作蒙特卡洛仿真和动态规划的结合。
3、在探索与利用发面,两者都使用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy策略进行策略的改进,并且策略改进的策略都是选择使得动作-值函数最大的动作。
不同点:
二者的最大区别在于,对于智能体的控制方法不同(大方法都是时序差分法)。这个控制方法的不同,决定了二者在实现强化学习任务上会存在区别。
算法实现关键点:
1、使用与状态维度一致的数组存储策略policy可以更方便;
2、q_table不一定要二维;
3、epsilon-greedy在动作选择时使用,在策略更新时不使用,可以更好地进行实现。
2 grid world
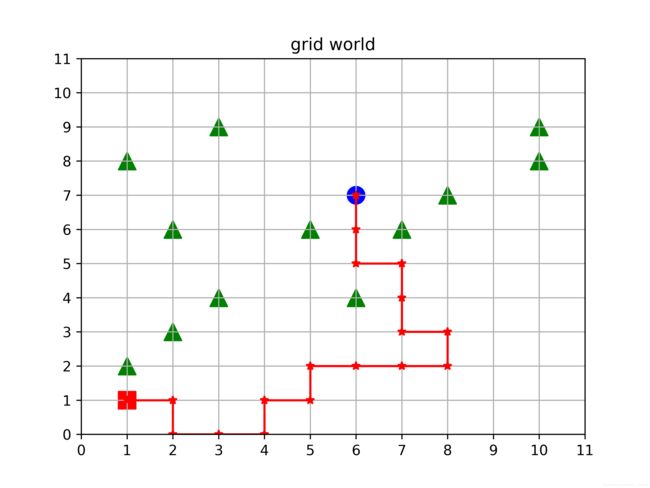
上图所示就是一个grid world问题,红色为出发点,蓝色为终止点,绿色为障碍物。整个问题的目的在于从出发点出发,绕开障碍物,以最短路径达到终止点。图中所示的结果就是不是最优结果。
3 Q-learning实现
以下整个代码块可以直接复制在单独一个文件中执行
import matplotlib.pyplot as plt
import random
import numpy as np
# 用于展示任务开始时的grid world长什么样子,方便确认解是不是最优
def plot_world(world, stone_list, start_position, final_position, result=None):
plt.figure(1)
plt.ylim([0, len(world)-1])
plt.xlim([0, len(world)-1])
plt.xticks([i for i in range(len(world))], [str(i) for i in range(len(world))])
plt.yticks([i for i in range(len(world))], [str(i) for i in range(len(world))])
plt.grid()
plt.title("grid world")
plt.scatter(start_position[0], start_position[1], s=150, color="red", marker="s")
plt.scatter(final_position[0], final_position[1], s=150, color="blue", marker="o")
for eve in stone_list:
plt.scatter(eve[0], eve[1], s=150, color="green", marker="^")
if result != None:
for i in range(len(result)-1):
plt.plot([result[i][0], result[i+1][0]], [result[i][1], result[i+1][1]], color="red", marker="*")
plt.savefig("qlearning-grid-result.png", dpi=600)
plt.show()
else:
plt.savefig("grid.png", dpi=600)
plt.show()
# 根据动作和当前状态,决定下一时刻的状态, max_trick为最大坐标值
def action_result(action, current_state, max_trick):
if action == "up":
if current_state[1] == max_trick:
return current_state
else:
return (current_state[0], current_state[1]+1)
elif action == "down":
if current_state[1] == 0:
return current_state
else:
return (current_state[0], current_state[1]-1)
elif action == "left":
if current_state[0] == 0:
return current_state
else:
return (current_state[0]-1, current_state[1])
elif action == "right":
if current_state[0] == max_trick:
return current_state
else:
return (current_state[0]+1, current_state[1])
else:
raise IOError
# 奖励函数的指定,十分重要!!!
def get_reward(state, final_position, stone_list, current_state):
if state == current_state:
return -3
if state == final_position:
return 10
elif state in stone_list:
return -10
else:
return -1
# 获得最大的q值
def get_maxq(qtable, state):
temp = []
for i in range(len(qtable)):
temp.append(qtable[i][state[0]][state[1]])
maxone = max(temp)
argmax = np.argmax(temp)
return maxone, argmax
def print_policy(policy_, stone_list, final_position):
with open('qlearning-policy.txt', "w", encoding="utf-8") as f:
for x in range(len(policy_)):
for y in range(len(policy_[x])):
if (x, y) in stone_list:
print("({},{}):{}".format(x, y, "障碍物"), end="; ", file=f)
print("({},{}):{}".format(x, y, "障碍物"), end="; ")
elif (x, y) == final_position:
print("({},{}):{}".format(x, y, "终点"), end="; ", file=f)
print("({},{}):{}".format(x, y, "终点"), end="; ")
else:
print("({},{}):{}".format(x, y, action[policy_[x][y]]), end="; ", file=f)
print("({},{}):{}".format(x, y, action[policy_[x][y]]), end="; ")
print("", file=f)
print("")
if __name__ == "__main__":
# 生成12*12大小的二维网格世界,且world[i][j] = (i, j)
world = [[(i,j) for j in range(12)] for i in range(12)]
# 设置11个障碍物
stone_list = [(6,4), (10,8), (1,2), (2,3), (5,6), (10,9), (1,8), (3,9), (9,5), (10,7), (9,2), (9,7), (6, 9),(8,7),(8,8),(8,9)]
# 设置入口与出口
start_position = (1, 1)
final_position = (9, 8)
# plot_world(world, stone_list, start_position, final_position)
# 动作
action = ["up", "down", "left", "right"]
# q-learning 算法解决grid world问题
# q table用于存储动作状态值 三位列表,初始值均为0
q_table = [[[0 for j in range(len(world))] for i in range(len(world))] for k in range(4)]
policy = [[0 for j in range(len(world))] for i in range(len(world))]
episodes = 600
alpha = 0.7
gamma = 0.5
epsilon = 0.5
for episode in range(episodes):
current_state = start_position
save = [current_state]
while True:
# 策略选择动作
if random.randint(1,100)/100 > epsilon:
action_index = policy[current_state[0]][current_state[1]]
else:
action_index = random.randint(0,3)
next_state = action_result(action[action_index], current_state, 11)
reward = get_reward(next_state, final_position, stone_list, current_state)
# 更新q值表
maxone, _ = get_maxq(q_table, next_state)
q_table[action_index][current_state[0]][current_state[1]] += \
alpha*(reward + gamma*maxone - q_table[action_index][current_state[0]][current_state[1]])
# 更新策略
_, argmax = get_maxq(q_table, current_state)
policy[current_state[0]][current_state[1]] = argmax
# 时间步长改变
current_state = next_state
save.append(current_state)
if reward == 10 or reward == -10:
# print(save)
break
# 进行推理
state = start_position
res = [state]
print("begin:", state, end=";")
for i in range(20):
a_index = policy[state[0]][state[1]]
next_state = action_result(action[a_index], state, 11)
print(next_state, end=";")
res.append(next_state)
if next_state == final_position:
print("bingo!")
print("共走了",i+1,"步")
plot_world(world, stone_list, start_position, final_position,res)
print("使用q-learning训练并推理产生的结果图见根目录'qlearning-grid-result.png'")
print("使用q-learning训练并推理产生的策略已保存在'qlearning-policy.txt'")
print("q-learning策略:")
print_policy(policy, stone_list, final_position)
break
state = next_state
4 Sarsa实现
算法基于CS234课程中的原文:

以下整个代码块可以直接复制在一个单独文件中直接执行
import matplotlib.pyplot as plt
import random
import numpy as np
# 用于展示任务开始时的grid world长什么样子,方便确认解是不是最优
def plot_world(world, stone_list, start_position, final_position, result=None):
plt.figure(1)
plt.ylim([0, len(world)-1])
plt.xlim([0, len(world)-1])
plt.xticks([i for i in range(len(world))], [str(i) for i in range(len(world))])
plt.yticks([i for i in range(len(world))], [str(i) for i in range(len(world))])
plt.grid()
plt.title("grid world")
plt.scatter(start_position[0], start_position[1], s=150, color="red", marker="s")
plt.scatter(final_position[0], final_position[1], s=150, color="blue", marker="o")
for eve in stone_list:
plt.scatter(eve[0], eve[1], s=150, color="green", marker="^")
if result != None:
for i in range(len(result)-1):
plt.plot([result[i][0], result[i+1][0]], [result[i][1], result[i+1][1]], color="red", marker="*")
plt.savefig("sarsa-grid-result.png", dpi=600)
plt.show()
else:
plt.savefig("grid.png", dpi=600)
plt.show()
# 根据动作和当前状态,决定下一时刻的状态, max_trick为最大坐标值
def action_result(action, current_state, max_trick):
if action == "up":
if current_state[1] == max_trick:
return current_state
else:
return (current_state[0], current_state[1]+1)
elif action == "down":
if current_state[1] == 0:
return current_state
else:
return (current_state[0], current_state[1]-1)
elif action == "left":
if current_state[0] == 0:
return current_state
else:
return (current_state[0]-1, current_state[1])
elif action == "right":
if current_state[0] == max_trick:
return current_state
else:
return (current_state[0]+1, current_state[1])
else:
raise IOError
# 奖励函数的指定,十分重要!!!
def get_reward(state, final_position, stone_list, current_state):
if state == current_state:
return -5
if state == final_position:
return 30
elif state in stone_list:
return -30
else:
return -5
# 获得最大的q值
def get_maxq(qtable, state):
temp = []
for i in range(len(qtable)):
temp.append(qtable[i][state[0]][state[1]])
maxone = max(temp)
argmax = np.argmax(temp)
return maxone, argmax
# 打印策略
def print_policy(policy_, stone_list, final_position):
with open('sarsa-policy.txt', "w", encoding="utf-8") as f:
for x in range(len(policy_)):
for y in range(len(policy_[x])):
if (x, y) in stone_list:
print("({},{}):{}".format(x, y, "障碍物"), end="; ", file=f)
print("({},{}):{}".format(x, y, "障碍物"), end="; ")
elif (x, y) == final_position:
print("({},{}):{}".format(x, y, "终点"), end="; ", file=f)
print("({},{}):{}".format(x, y, "终点"), end="; ")
else:
print("({},{}):{}".format(x, y, action[policy_[x][y]]), end="; ", file=f)
print("({},{}):{}".format(x, y, action[policy_[x][y]]), end="; ")
print("", file=f)
print("")
if __name__ == "__main__":
# 生成12*12大小的二维网格世界,且world[i][j] = (i, j)
world = [[(i,j) for j in range(12)] for i in range(12)]
# 设置11个障碍物
stone_list = [(6,4),(8,4),(6,3),(1,2),(6,1),(6,2),(6,0),
(2,3), (5,6), (10,2),(1,8), (3,9),(8,7), (8,5),(8,3),(8,8),(9,9),(9,7)]
# 设置入口与出口
start_position = (1, 1)
final_position = (9, 8)
# plot_world(world, stone_list, start_position, final_position)
# 动作
action = ["up", "down", "left", "right"]
# q table用于存储动作状态值 三位列表,初始值均为0
q_table = [[[0 for j in range(len(world))] for i in range(len(world))] for k in range(4)]
policy = [[0 for j in range(len(world))] for i in range(len(world))]
# sarsa 算法解决grid world问题
episodes = 1000
alpha = 0.7
gamma = 0.5
for episode in range(episodes):
epsilon = 1 / (episode + 1)
current_state = start_position
save = [current_state]
# 策略选择动作 a t
if random.randint(1, 100) / 100 > epsilon:
action_index = policy[current_state[0]][current_state[1]]
else:
action_index = random.randint(0, 3)
next_state = action_result(action[action_index], current_state, 11) # S_t+1
reward = get_reward(next_state, final_position, stone_list, current_state) # R_t
# sarsa用整个episode来更新一个策略
while True:
# 获取a t+1
if random.randint(1, 100) / 100 > epsilon:
action_index2 = policy[next_state[0]][next_state[1]]
else:
action_index2 = random.randint(0, 3)
# 获取s t+2 和 r t+1
next_state2 = action_result(action[action_index2], next_state, 11) # S_t+2
reward2 = get_reward(next_state2, final_position, stone_list, next_state) # R_t+1
# sarsa更新q值表
q_table[action_index][current_state[0]][current_state[1]] += \
alpha*(reward + gamma*q_table[action_index2][next_state[0]][next_state[1]] - q_table[action_index][current_state[0]][current_state[1]])
# 更新策略
_, argmax = get_maxq(q_table, current_state)
policy[current_state[0]][current_state[1]] = argmax
save.append(current_state)
# print(current_state)
if reward == 30 or reward == -30:
# print(save)
break
# 时间步长改变
reward = reward2
current_state = next_state
next_state = next_state2
action_index = action_index2
# 进行推理
begin = start_position
state = begin
res = [state]
print("begin:", state, end=";")
for i in range(25):
a_index = policy[state[0]][state[1]]
next_state = action_result(action[a_index], state, 11)
print(next_state, end=";")
res.append(next_state)
if next_state == final_position:
print("bingo!")
print("共走了",i+1,"步")
plot_world(world, stone_list, begin, final_position, res)
print("使用sarsa训练并推理产生的结果图见根目录'sarsa-grid-result.png'")
print("使用q-learning训练并推理产生的策略已保存在'sarsa-policy.txt'")
print("sarsa策略:")
print_policy(policy, stone_list, final_position)
break
state = next_state
5 总结
1、Q-learning与sarsa这两种算法的收敛速度很快,无论障碍物设置多么复杂,都能很快地找到最优解,在源码中可以任意设置障碍物与起始点和终止点的。
2、奖励函数对于结果会产生比较大的影响。本次的奖励函数主要是离散分段的奖励函数,到达目标正奖励最大,到达障碍负奖励最大,每走一步都会有-1的奖励,以确保其能够尽快地走到终点。可以说智能的体现很大程度取决于奖励函数的设计。
3、相比Sarsa,Q-learning算法的选择要更加大胆,试错能力更强,并且当Sarsa的epsilon没有随时间衰减的话,得到的解也不是最优解。总的来说,Q-learning算法在解决grid world问题中较好。
