机器学习笔记(十一)——学支持向量机怎能不懂“核“
非线性支持向量机
对于线性分类问题,线性分类支持向量机是一种非常有效的方法。但是有的分类问题是非线性的,这时就可以使用非线性支持向量机对分类问题求解,其主要的特点是利用核技巧(kernel trick),下面通过一个通俗的小栗子介绍核技巧。
核方法与核技巧
假设有一个二维平面上有4个点,两个红色点、两个绿色点,这4个点位于一条直线上,如下:

对于这个问题,我们是无法利用一条直线准确将红色点和绿色点分隔开,但是可以利用一条曲线实现分类,如下:

这时可以改变一下我们固有的思想,如果将二维平面映射至三维立体空间中,并且将一类别的点在纵轴上提高或者下降,这样不就可以利用一个超平面将其分隔开了嘛!如下:

现在只需要考虑一个问题,就是将同一类别在纵轴上同时提高或下降的操作应该如何实现。先回到开始的二维平面,如果将这些点添至坐标轴中,会不会存在某个函数的图像可以将其分隔开呢?
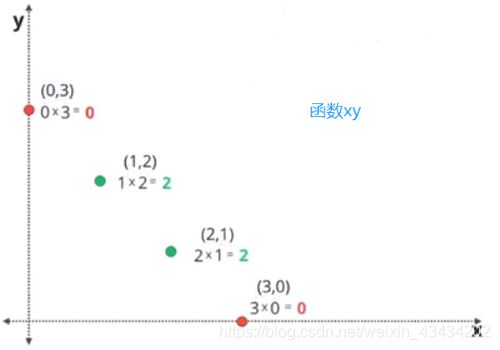
| (x,y) | (0,3) | (1,2) | (2,1) | (3,0) |
|---|---|---|---|---|
| xy | 0 | 2 | 2 | 0 |
这里利用一个函数 x y xy xy区分两类点,可以看出红色点的横纵坐标乘积为0,即 x y = 0 xy=0 xy=0,绿色点的横纵坐标乘积为2,即 x y = 2 xy=2 xy=2,那么利用曲线 x y = 1 xy=1 xy=1不就可以将两类点准确分类嘛!如下:

其中 x y = 1 xy=1 xy=1也就是我们非常熟悉的反比例函数 y = 1 x y=\frac{1}{x} y=x1。
解决了二维平面的问题,那么再将其映射至三维空间就可以解决前文提出的问题了。可以将 x y = 1 xy=1 xy=1算出的新值作为点在三维空间的z轴的坐标,绿色的点就可以沿z轴正方向提高,两类点就可以利用一个超平面实现分类,如下:

上面这个栗子也称作异或问题,求解这个问题利用的思想就是核方法。
这个栗子说明用线性分类方法求解分线性分类问题大致可分为两步:首先使用一个变换将原空间的数据映射至新空间;然后在新空间里用线性分类学习方法对数据进行分类,核技巧就属于这样的方法。
核技巧的基本思想就是通过一个非线性变换将输入空间映射至特征空间,使得输入空间的超曲面模型对应于特征空间的超平面模型,这样,就可以通过在特征空间利用线性支持向量机求解分类问题。
核函数
在知道核技巧的基本思想后,我们可以对之前求出的对偶问题做出相应的处理,即通过输入空间向特征空间的映射,将 x i → ϕ ( x i ) 、 x j → ϕ ( x j ) x_i\to\phi(x_i)、x_j\to\phi(x_j) xi→ϕ(xi)、xj→ϕ(xj),如下:

若按照这种方法对问题求解,必须在特征空间中求出 ϕ ( x i ) \phi(x_i) ϕ(xi)和 ϕ ( x j ) \phi(x_j) ϕ(xj)的内积,但是特征空间的维度往往是比较大的,这就使内积的运算极其复杂,有没有另一种方法可以简化这个求解方式呢?
假设有一个二维平面,我们需要将其映射至一个三维特征空间中,那么二维平面上的两类样本点分为用 ( x 1 , x 2 ) (x_1,x_2) (x1,x2)和 ( x 1 ∗ , x 2 ∗ ) (x_1^*,x_2^*) (x1∗,x2∗);则在三维特征空间中两类点可以用 ( z 1 , z 2 , z 3 ) (z_1,z_2,z_3) (z1,z2,z3)和 ( z 1 ∗ , z 2 ∗ , z 3 ∗ ) (z_1^*,z_2^*,z_3^*) (z1∗,z2∗,z3∗)表示。
若要对三维特征空间做内积操作,可以将其做以下推导,可以看到三维特征空间中的内积是可以由二维平面的内积表示的,最后得到的这个函数就被称为核函数。
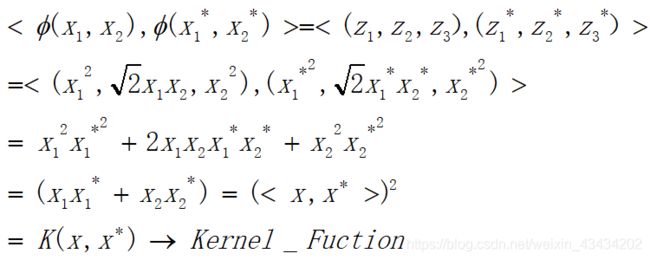
所以对于每一个映射至特征空间中的函数,都可以找到一个相应的核函数对其运算进行优化,表达式也可以做出相应的更改,如下:

在此基础上可以了解一下核函数的定义,设 χ \chi χ是输入空间,又设 H H H为特征空间(希尔伯特空间),如果存在一个 χ \chi χ到 H H H的映射 ϕ ( x ) : χ → H \phi(x):\chi\to{H} ϕ(x):χ→H使得对所有 x , z ∈ χ x,z\in\chi x,z∈χ,函数 K ( x , z ) K(x,z) K(x,z)满足条件 K ( x , z ) = ϕ ( x ) ⋅ ϕ ( z ) K(x,z)=\phi(x)\cdot\phi(z) K(x,z)=ϕ(x)⋅ϕ(z)则称 K ( x , z ) K(x,z) K(x,z)为核函数, ϕ ( x ) \phi(x) ϕ(x)为映射函数,其中 ϕ ( x ) ⋅ ϕ ( z ) \phi(x)\cdot\phi(z) ϕ(x)⋅ϕ(z)为 ϕ ( x ) \phi(x) ϕ(x)和 ϕ ( z ) \phi(z) ϕ(z)的内积。
综上,如果有一个待求解的非线性分类问题,我们没有必要去计算其对应特征空间中的内积,只需要找到这个非线性分类问题对应的核函数,将输入空间的数据代入核函数中,便可求得该问题的解。
于是,“核函数的选择”就成了支持向量机的最大变数,若核函数的选择不合适,则意味着将样本映射到了一个不合适的特征空间,很可能导致分类效果不佳。而 ϕ ( x ) \phi(x) ϕ(x)只是起到一个中间的过渡作用,并没有什么实际意义。
下图给出了几个常用的核函数,其中高斯核函数是最为重要的,也称作径向基核函数。

正定核
在已知映射函数 ϕ \phi ϕ,可以通过 ϕ ( x ) \phi(x) ϕ(x)和 ϕ ( z ) \phi(z) ϕ(z)的内积求得核函数 K ( x , z ) K(x,z) K(x,z),但这个过程是比较复杂的,能否直接判断一个给定的函数是不是核函数呢?或者一个函数需要满足什么条件才能成为核函数?
我们通常所说的核函数是叫作正定核函数,先了解一下正定核的两个概念。
其一,若输入空间 χ \chi χ映射至特征空间 H H H的关系为 ϕ \phi ϕ K : χ × χ → R K:\chi\times\chi\to R K:χ×χ→R ∀ ( x , z ) , 有 K ( x , z ) \forall(x,z),有K(x,z) ∀(x,z),有K(x,z) ∃ ϕ 使 得 K ( x , z ) = < ϕ ( x ) ⋅ ϕ ( z ) > \exists\phi使得K(x,z)=<\phi(x)\cdot\phi(z)> ∃ϕ使得K(x,z)=<ϕ(x)⋅ϕ(z)> 则称 K ( x , z ) K(x,z) K(x,z)为正定核函数。
R代表数学中的实数域
其二,对于输入空间 χ \chi χ内的样本点 K : χ × χ → R K:\chi\times\chi\to R K:χ×χ→R ∀ ( x , z ) , 有 K ( x , z ) \forall(x,z),有K(x,z) ∀(x,z),有K(x,z) 如果 K ( x , z ) K(x,z) K(x,z)满足对称性和正定性,则称 K ( x , z ) K(x,z) K(x,z)为正定核函数。
概念一很好理解,并且前文也应用到了,所以这里着重讲述一下概念二。概念二的对称性: K ( x , z ) = K ( z , x ) K(x,z)=K(z,x) K(x,z)=K(z,x) 由于内积运算具有对称性,而核函数包含内积运算,所以核函数具有对称性。
正定性表示对于任意 x i ∈ χ , i = 1 , 2... n x_i\in\chi,i=1,2...n xi∈χ,i=1,2...n, K ( x , z ) K(x,z) K(x,z)对应的Gram矩阵 K = [ K ( x i , x j ) ] n × n K=[K(x_i,x_j)]_{n\times n} K=[K(xi,xj)]n×n 是半正定矩阵。如果在对称性成立的情况下,那么正定性是一个核函数为正定核的充要条件,即 K ( x , z ) = ϕ ( x ) ⋅ ϕ ( z ) ⟺ G r a m 矩 阵 半 正 定 K(x,z)=\phi(x)\cdot\phi(z)\iff Gram矩阵半正定 K(x,z)=ϕ(x)⋅ϕ(z)⟺Gram矩阵半正定
详细过程可见《统计学习方法》P121-122
这里只给出必要性的证明。若要证明一个矩阵是半正定的,只需证明矩阵中每个特征值都大于等于0即可。在已知条件下,对任意的 c 1 , c 2 . . . c n ∈ R c_1,c_2...c_n\in R c1,c2...cn∈R,若存在以下等式:
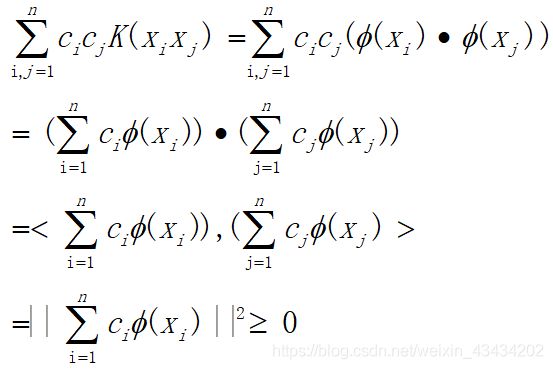
则表明 K ( x , z ) K(x,z) K(x,z)关于 x i x_i xi的Gram矩阵是半正定的。
总结
对于分类问题而言,可以利用核技巧,将线性分类的学习方法应用至非线性分类问题中。将线性支持向量机扩展至非线性支持向量机,只需将线性支持向量机对偶问题中的内积利用转化成核函数即可。至此,SVM中的三宝间隔对偶核函数都已经介绍完毕。
关注公众号【喵说Python】获取每篇文章的源码和数据,欢迎各位伙伴和博主交流呀。