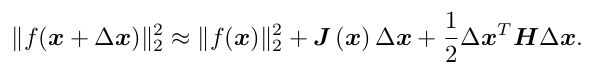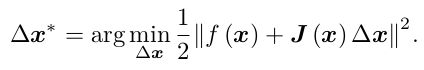透彻理解SLAM中的非线性最小二乘问题

下面是我从yuque复制过来的，格式有些问题，需要的可以直接看我笔记原文：

https://www.yuque.com/docs/share/61fb4428-e631-4b96-b531-b3b09cdb1a44?# 《【系统】透彻理解SLAM中的非线性优化问题-理论》

Q：最小二乘法在SLAM系统中具体解决什么问题？

A：SLAM问题实质上是一个由各种观测估计传感器运动（位姿）的状态估计（后验估计）问题。换个说法就是，在传感器观测数据构建的约束中，寻找一个传感器的最优位姿估计。在这个大问题下，不同的传感器有不同的观测模型，有不同的约束构建方法，但最后都是通过观测数据去求位姿这样一个过程。求解的方法有基于优化的，基于滤波的方法。对于基于优化的方法来说，一般的SLAM系统都是非线性的，而非线性最小二乘法就是非线性优化问题的一个求解方法，也是现在SLAM系统中采用比较多的方法。基于滤波的方法，滤波是用于估计当前的状态，如果我们之前的数据出现错误，是没有办法进行修正的，所以这个方法的整体效果并不是特别好。

1 非线性最小二乘

定义如下形式为最小二乘法的表示：

 

 

上式中，x为状态量，f(x)为关于x的残差函数，我们的目的是找到合适的x*使得F(x*)最小；

现在有两种情况：

1. 如果f(x)为线性函数，这就是线性最小二乘问题，一些简单的线性最小二乘问题,可以通过对F(x)求导并令其等于0的方式可以找到极小值点
2. 如果f(x)为非线性函数,一些复杂的非线性最小二乘问题利用\frac{dF}{dx}=0这种方式求解需要我们知道目标函数的全局性质,这一般不太可能，这时我们采用迭代法的方式来求x'使得F(x')无限接近F(x*)。

第二种情况，显然是SLAM系统更关心的问题，也是本文的重点。

也就是说，我们要利用迭代法来求解我们构建的非线性最小二乘问题。

1.1 迭代法与\Delta{}x

迭代法,就是从一个初始值出发,通过不断的更新当前的优化变量,使目标函数不断下降,达到一定阈值的时候,可以用当前的优化变量大小近似代替最优的变量值,这样就问题从对F(x)求导,转换到了不断寻找dx使得F(x+dx) < F(x)这样一个过程了

迭代法的步骤：

 

根据上面的步骤,我们能看出,迭代法的几个关键核心问题:

1. 如何确定较好的初始值
2. 每一步如何寻找\Delta{x}
   使得||f(x_k+\Delta{x})||_2^2达到极小值
3. 什么时候迭代停止

对于第一个问题,不同的问题有不同的解决方法,会有一些估计值作为初始值,一些算法对初始值比敏感,SLAM算法的配准时,就涉及到初始值的问题,目前还未过于关注,后面补充.

第三个问题解决的方法主要有判断dx大小,和dF两种

第二个问题便是众多不同方法的最主要的区别,就是\Delta{}x该如何获得,下面就来说一下不同的方法.

Q:那这样的处理是否就不用对F(x)求导了呢?

A:并不是,还是需要求导,只不过不再关系F(x)的全局性质

1.2 \Delta{}x与\alpha*\Delta{}x

1.1中说来优化变量的更新方程是x_{k+1}=x_k + \Delta{x_k},实际上,一些算法还会给求得的\Delta{}x乘上一个步长\alpha
,用来更加灵活的控制每次的增量大小.同时也有一些选择\alpha
的方法,这里说一个line-search的方法,

*line-search:

前提:\Delta{}x已经确定

F(x+\alpha*d) \approx F(x) +\alpha{}Jd-----(一阶泰勒展开)

使

F(x+\alpha{d}) < F(x)
=>
\alpha{}Jd<0=>Jd<0

1.3 最速下降法(一阶梯度法)与牛顿法(二阶梯度法)

后面的各种方法也都是最速下降法的一种改良,其核心思想没变,这里重点讲一下最速下降法,后面的主要说改良的地方.

1.3.1 为什么要泰勒展开?

前面提到过,求解\frac{dF}{dx}=0问题时,需要知道F(x)的全局性质,这一般不可行,所以我们换种思路,在x附近利用泰勒展开,将F(x)表示为如下的形式:

上式J为F(x)关于其变量x的一阶导数,即雅可比矩阵,也叫梯度,H为二阶导数海塞矩阵.

换种方式表达,可能更好理解:

l(\Delta{x})=||f(x_k)||_2^2+J(x_k)\Delta{x}+\frac{1}{2}\Delta{x}^TH(x_k)\Delta{x}

即上面的雅可比与海塞矩阵在某一次迭代过程中为常数,优化函数变成了关于\Delta{}x线性函数(只保留一阶项时),或者二次函数(保留二阶项时),这也是我们为什么要使用泰勒展开的原因:

我们通过泰勒展开将目标函数在当前x附近拟合成线性或者二次函数,方便我们求得\Delta{}x.

1.3.2 如何求增量?

• 对于一阶梯法:

取增量为反向的梯度即可保证函数下降:

• 对于二阶梯度法(牛顿法):

类似于二次函数求极小值,对l(dx)关于dx求导并令其等于0,可以得到:

求解上面的方程就得到了增量

1.4高斯牛顿法GN

再说GN之前,再明确一下符号含义:

\min \limits_{x}F(x) = \frac{1}{2}||f(x)||^2

F(x)表示待优化的目标函数,f(x)表示残差函数,一二阶梯度法是对F(x)进行泰勒展开,而高斯牛顿的核心思想是对f(x)进行泰勒展开:

此时,我们的优化问题变为了寻找下降矢量 ∆x,使得||f (x + ∆x)∥^2 达到最小:

而:

上式右侧为关于dx的二次函数,又转换成了求二次函数极小值的问题,只需要对上述函数关于dx求导并令其等于0,可得:

即:

解方程可得增量,对比于牛顿法,GN使用f(x)的J^TJ近似替代了牛顿法中F(x)的H

1.5阻尼牛顿法与列文伯格-马夸尔特法

1.5.1 阻尼牛顿法

牛顿法的增量方程为:

\Delta{x}=\argmin \limits_{\Delta{x}}(F(x)+J\Delta{x}+\frac{1}{2}\Delta{x}^TH\Delta{x})

阻尼牛顿法的改进是在,待优化函数后面加一个惩罚项:

\Delta{x}=\argmin \limits_{\Delta{x}}(F(x)+J\Delta{x}+\frac{1}{2}\Delta{x}^TH\Delta{x})+\frac{1}{2}\mu\Delta{x}^T\Delta{x}) ---(\mu>=0)

对上式右侧关于dx求导,并令其为0,有:

J+H\Delta{x}+\mu\Delta{x}=0\\

\\

(H+\mu I)\Delta{x}=-J

阻尼因子\mu可以根据dx的值进行调整,他有比较多的好处,在下节讲.

1.5.2LM

类似于阻尼牛顿法,LM可以看作是阻尼高斯牛顿法下面直接给出LM方法的增量方程:

(J^TJ+\mu I)\Delta{x} = -J^Tf(x_k)

那这个阻尼因子有什么好处呢?

也就是说,除了保证正定外,通过调节阻尼因子可以在不同的阶段分别利用不同方法的优点,保证算法的效率和收敛

那么如何调节阻尼因子呢?

• 阻尼因子初始值的选取

• 阻尼因子的更新

1. 阻尼更新的马夸尔特策略

1. 阻尼更新的Nieslen策略

2 各种方法优缺点对比

方法	增量方程H\Delta{x}=g	优点	缺点
最速下降法	\Delta{x}^*=-J(x_k)	计算简单	容易震荡导致收敛慢
牛顿法	H(x_k)\Delta{x}^*=-J(x_k)	拟合更加准确	H的计算比较困难
高斯牛顿法	J(x_k)J^T(x_k)\Delta{x}^*=-J(x_k)f(x_k)	不用计算H	JTJ可能半正定,导致病态
L-M	(JJ^T+\mu I)\Delta{x}^*=-J(x_k)f(x_k)	动态调整阻尼,拥有上面的优点	表达形式复杂