李宏毅机器学习 之 神经网络训练不起来怎么办（五）

目录

一、局部最小值 Local Minima 与鞍点 Saddle point

1、为什么Saddle point 和 Local Minima 不好优化？

2、如何区分 Saddle point 和 Local Minima ？

二、批次 Batch 与动量法 Momentum

1、Batch 和Epoch

1）随机梯度下降 Stochastic Gradient Descent

2）小批量梯度下降 Mini-batch Gradient Descent

3）全批量梯度下降 Batch Gradient Descent

2、Small Batch 和 Large Batch

3、动量梯度下降法 Momentum

三、自动调整学习率 Learning rate

1、AdaGrad 优化算法

2、RMSProp 优化算法

3、Adam 优化算法

四、损失函数Loss 也有可能影响

1、回归 Regression 和 分类 Classification

2、MSE和 Cross-entropy 的区别

五、批次标准化 Batch-Normalization

---

一、局部最小值 Local Minima 与鞍点 Saddle point

1、为什么Saddle point 和 Local Minima 不好优化？

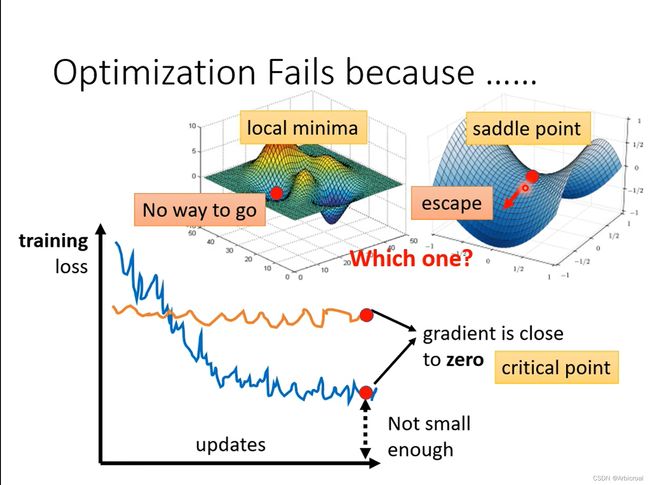
鞍点：在微分方程中，沿着某一方向是稳定的，另一条方向是不稳定的奇点，叫做鞍点。在泛函中，既不是极大值点也不是极小值点的临界点，叫做鞍点。在矩阵中，一个数在所在行中是最大值，在所在列中是最小值，则被称为鞍点。可以理解为“马背”上的点，下图蓝色图中的红点就是鞍点。

鞍点和局部最小点都是临界点critical point，此处的梯度都为0，所以在优化的时候很容易陷在其中，无法收敛到全局最小点。

 

2、如何区分 Saddle point 和 Local Minima ？

要区分局部极小点和鞍点，需要用到Hessian 矩阵。

当 H > 0，说明特征值全部为正，此点为局部极小点；

当 H < 0，说明特征值全部为负，此点为局部极大点；

当 H 有时大于0，有时小于0，说明此点为鞍点；

但是Hessian 矩阵不仅需要计算梯度，还需要计算Loss对weight的二阶偏导数，计算量非常大，所以不建议使用这种方法。

 

二、批次 Batch 与动量法 Momentum

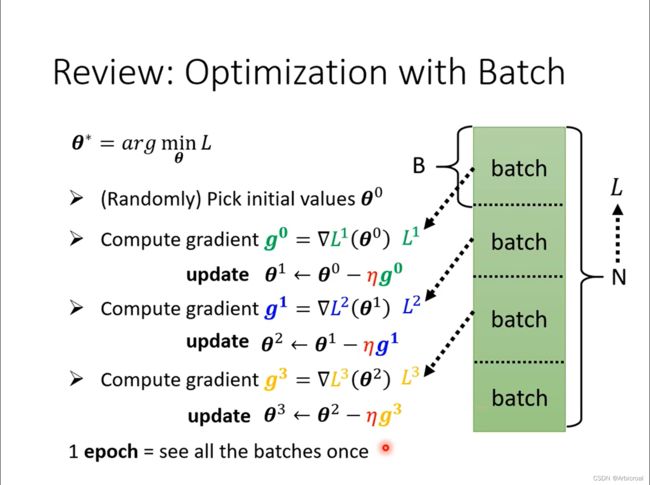
1、Batch 和Epoch

1个epoch相当于所有的batch过一遍，并且epoch之后要shuffle一下。

batch是将整体样本分成若干份，按大小可以分为三种：随机梯度下降、小批量梯度下降和全批量梯度下降。

设样本数为m，

1）随机梯度下降 Stochastic Gradient Descent

每次从样本中随机选择一个进行学习，batch size = 1

优点：学习速度快；

缺点：优化波动，收敛变慢。

2）小批量梯度下降 Mini-batch Gradient Descent

每次从样本中随机选择部分进行学习，1 < batch size < m

if mini-batch size = 1：即为随机梯度下降；

if mini-batch size = m：即为全批量梯度下降；

优点：学习速度快，朝着极小点方向。

3）全批量梯度下降 Batch Gradient Descent

每次使用全部的样本进行学习，batch size = m

优点：必然能收敛到极小点；

缺点：学习速度非常慢。

 

2、Small Batch 和 Large Batch

Small Batch 和 Large Batch 我感觉是根据样本个数来判断的，样本不是很大的时候batch的大小对时间没有很大影响，时间差不多。

当样本数很大的时候，batch还是设置的稍大一些较好。有GPU可以平行计算的话，也可以把batch设置的大一点。

 

3、动量梯度下降法 Momentum

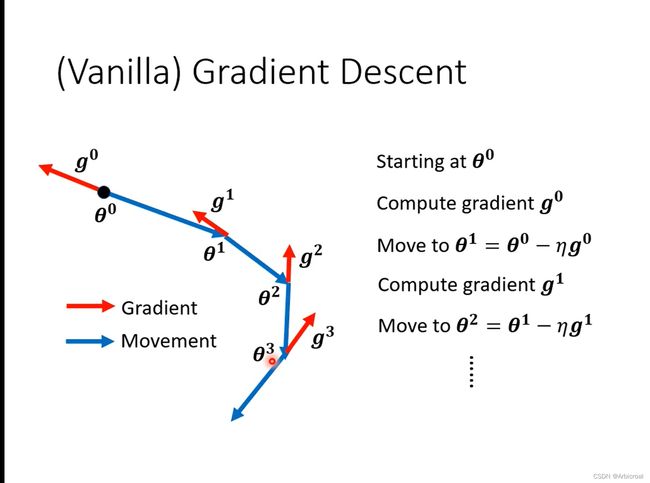
动量梯度下降法是在梯度下降法的基础上，引入物理上的动量，之前的梯度下降是下图的样子，只考虑梯度和步长。

 

改进后的动量梯度下降法在考虑梯度和步长的同时，还参考前一步的更新方向。

如下图所示，新的移动方向是梯度的反方向和最新一步的更新方向相加之后的方向。

 

三、自动调整学习率 Learning rate

1、AdaGrad 优化算法

特点：每次使用不同的学习率；

缺点：由于累积梯度的平方，可能导致梯度消失。

更新公式如下图所示：

 

2、RMSProp 优化算法

先将权重和偏置的微分平方，再开方。为确保分母不为0，在分母上加上一个 ，很小的值，

更新公式：

3、Adam 优化算法

Adam 优化算法 全称是自适应动量估计 Adaptive Momentum estimation

实际是将Momentum 和 RMSProp法结合在一起。

四、损失函数Loss 也有可能影响

1、回归 Regression 和 分类 Classification

分类和回归做的事情都差不多，不同的是最后输出结果，分类输出的 y 是向量，不是数值，最后的  要把 y 经过一个softmax函数再输出，使  的值在0~1之间。

 

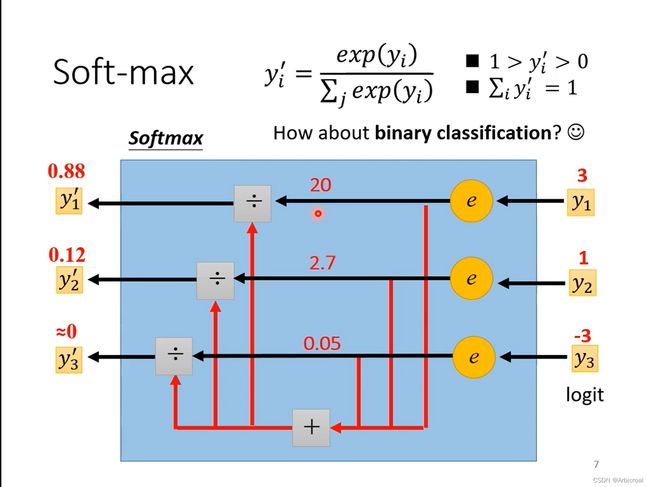
softmax函数的处理流程如下图所示：

公式：

        

        

 

2、MSE和 Cross-entropy 的区别

MSE全称Mean Square Error 。二者主要在公式更新上不同。

Mean Square Error 更新公式：

Cross-entropy 更新公式：

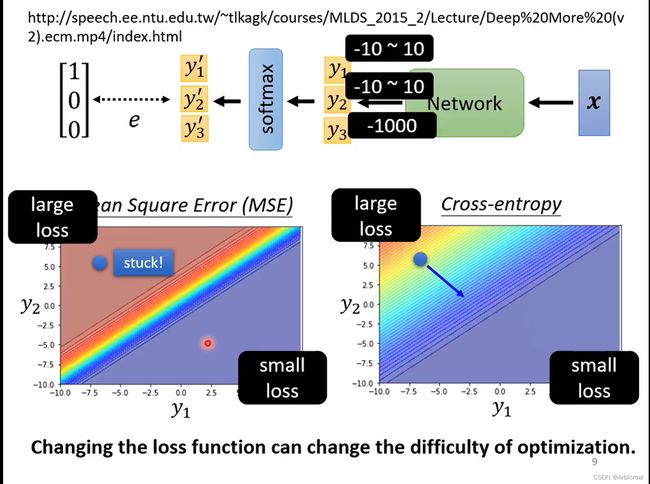
下面是一个例子说明两个Loss的不同，当y1 、y2、 y3 输入不同的值，令y3 很小，这样经过exp之后对没什么影响，几乎为0，主要为了观察 y1 和 y2 ，途中蓝色代表loss很小的区域，红色代表Loss很大的区域，假设开始的地方都是loss很大的地方（图中蓝色的点），当使用Cross-entropy 有斜率，会让梯度朝着loss很小的方向下降；但是MSE会卡住，在Loss很大的地方，梯度很小，很难朝着loss小的方向下降，可以设置自动调整学习率来改变步长，也是有可能走到Loss小的地方。

 

五、批次标准化 Batch-Normalization

Batch-Normalization 不适合batch size很小的情况，Batch-Normalization可以保证无论怎样变化，Z的均值和方差保持不变。

当在测试集上Batch-Normalization，需要加入参数再次调整Z。