Python时间序列分析3-非平稳序列的随机分析-SRARIMA

import pandas as pd 
import matplotlib.pyplot as plt 
import numpy as np
from datetime import datetime,timedelta
from time import time

数据读取与预处理

cat_fish = pd.read_csv('./data/catfish.csv',parse_dates=[0],index_col=0,squeeze=True)

cat_fish.head()

Date
1986-01-01     9034
1986-02-01     9596
1986-03-01    10558
1986-04-01     9002
1986-05-01     9239
Name: Total, dtype: int64

时序图

plt.plot(cat_fish)

[]

序列有明显的趋势性

start = datetime(2000,1,1)
end = datetime(2004,1,1)
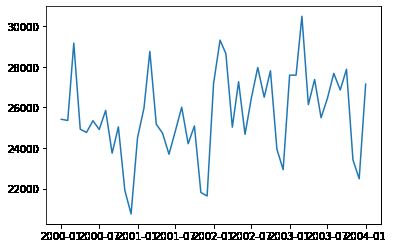
plt.plot(cat_fish[start:end])

[]

有很明显周期性

自相关系数图

from statsmodels.graphics.tsaplots import plot_acf,plot_pacf

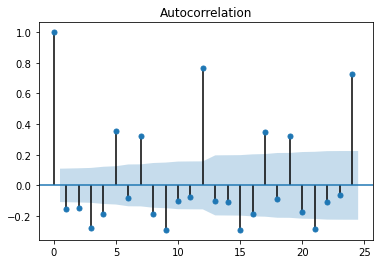
plot_acf(cat_fish.diff(1)[1:],lags=24)

偏自相关系数图

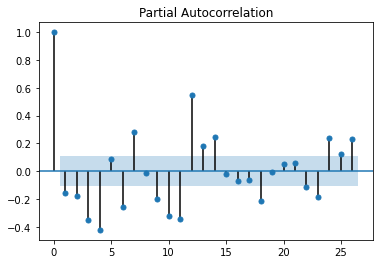
plot_pacf(cat_fish.diff(1)[1:])

偏自相关系数图12步差分时，相关系数比较大，剔除趋势性后，原始数据还是呈现出明显的周期性

白噪声检验

from statsmodels.stats.diagnostic import acorr_ljungbox

acorr_ljungbox(cat_fish.diff(1)[1:],lags=[6,12,18,24],return_df=True)

	lb_stat	lb_pvalue
6	95.719733	1.957855e-18
12	373.541488	1.498233e-72
18	466.300398	1.243989e-87
24	731.756632	5.126647e-139

不是白噪声

使用SARIMA(0,1,0)x(1,0,1,12)进行预测

(0,1,0)是一阶差分，提取趋势性信息
(1,0,1,12)是ARMA(1,1),季节周期为12，提取季节性信息

模型训练

from statsmodels.tsa.statespace.sarimax import SARIMAX

print(cat_fish.index[0],cat_fish.index[-1])

1986-01-01 00:00:00 2012-12-01 00:00:00

train_end = datetime(2009,1,1)
test_end = datetime(2010,1,1)
train_data = cat_fish[:train_end]
test_data = cat_fish[train_end + timedelta(days=1):test_end]

model = SARIMAX(train_data,order=(0,1,0),seasonal_order=(1,0,1,12))

model_fit = model.fit()

model_fit.summary()

C:\Users\lipan\anaconda3\lib\site-packages\statsmodels\tsa\base\tsa_model.py:159: ValueWarning: No frequency information was provided, so inferred frequency MS will be used.
  warnings.warn('No frequency information was'
C:\Users\lipan\anaconda3\lib\site-packages\statsmodels\tsa\base\tsa_model.py:159: ValueWarning: No frequency information was provided, so inferred frequency MS will be used.
  warnings.warn('No frequency information was'

SARIMAX Results

Dep. Variable:	Total	No. Observations:	277
Model:	SARIMAX(0, 1, 0)x(1, 0, [1], 12)	Log Likelihood	-2296.563
Date:	Sat, 03 Apr 2021	AIC	4599.126
Time:	17:13:59	BIC	4609.988
Sample:	01-01-1986	HQIC	4603.485
	- 01-01-2009
Covariance Type:	opg

	coef	std err	z	P>|z|	[0.025	0.975]
ar.S.L12	0.9889	0.007	135.425	0.000	0.975	1.003
ma.S.L12	-0.7923	0.054	-14.692	0.000	-0.898	-0.687
sigma2	9.069e+05	7.77e+04	11.666	0.000	7.55e+05	1.06e+06

Ljung-Box (Q):	71.38	Jarque-Bera (JB):	0.57
Prob(Q):	0.00	Prob(JB):	0.75
Heteroskedasticity (H):	2.47	Skew:	0.08
Prob(H) (two-sided):	0.00	Kurtosis:	3.16

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

预测

predictions = model_fit.forecast(len(test_data))
predictions = pd.Series(predictions,index=test_data.index)
residuals = test_data - predictions

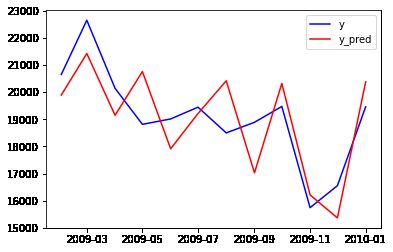
plt.plot(test_data,color ='b',label = 'y')
plt.plot(predictions,color='r',label='y_pred')
plt.legend()
plt.show()

残差图

plt.plot(residuals)

[]

残差白噪声检验

acorr_ljungbox(residuals,lags=10,return_df=True)

	lb_stat	lb_pvalue
1	2.974643	0.084579
2	3.702085	0.157073
3	9.938764	0.019094
4	16.441791	0.002480
5	16.607813	0.005307
6	17.906828	0.006469
7	21.149384	0.003555
8	21.996374	0.004923
9	22.067707	0.008667
10	22.789588	0.011550

循环预测

predictions_new = test_data.copy()
for train_end in test_data.index:
    train_data = cat_fish[:train_end-timedelta(days = 1)]
    model = model = SARIMAX(train_data,order=(0,1,0),seasonal_order=(1,0,1,12),freq='MS')
    model_fit = model.fit() 
    pred = model_fit.forecast(1)
    predictions_new[train_end] = pred

plt.plot(test_data,color ='b',label = 'y')
plt.plot(predictions_new,color='r',label='y_pred')
plt.legend()
plt.show()

plt.plot(test_data-predictions_new)

[]

print('RMSE:', np.sqrt(np.mean(residuals**2)))

RMSE: 1832.9537663585463

residuals_new = test_data-predictions_new
print('RMSE:', np.sqrt(np.mean(residuals_new**2)))

RMSE: 1242.0409950292837