SVD算法

SVD算法

以下内容来源于参考文献，仅供学习交流

一、什么是SVD算法

奇异值分解(Singular Value Decomposition，以下简称SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石

二、SVD算法的应用

隐形语义索引：最早的SVD应用之一就是信息检索，我们称利用SVD的方法为隐性语义检索（LSI）或隐形语义分析（LSA）。
基于SVD的图像压缩、基于协同过滤的推荐引擎、利用SVD简化数据
可应用于优化类问题，路径、空间最优化问题

三、SVD代码的实现

import math
import random
import matplotlib.pyplot as plt

#求平均值
def Average(fileName):
fi = open(fileName, ‘r’)
result = 0.0
cnt = 0
for line in fi:
cnt += 1
arr = line.split()
result += int(arr[2].strip())
return result / cnt

#计算矩阵点积
def InerProduct(v1, v2):
result = 0
for i in range(len(v1)):
result += v1[i] * v2[i]

return result

‘’’
定义预测评分计算式
参数声明：
av：平均值
bu: 用户评分与用户平均的偏差
bi: 项目评分与项目平均的偏差
pu: 用户特征矩阵
qi: 项目特征矩阵
‘’’
def PredictScore(av, bu, bi, pu, qi):
pScore = av + bu + bi + InerProduct(pu, qi)
if pScore < 1:
pScore = 1
elif pScore > 5:
pScore = 5

return pScore

def SVD(configureFile, testDataFile, trainDataFile, modelSaveFile):
# 从congigure文件中得到用户数、项目数、特征维度、学习率以及正则参数
fi = open(configureFile, ‘r’)
line = fi.readline()
arr = line.split()
averageScore = float(arr[0].strip())
userNum = int(arr[1].strip())
itemNum = int(arr[2].strip())
factorNum = int(arr[3].strip())
learnRate = float(arr[4].strip())
regularization = float(arr[5].strip())
fi.close()

# 初始化模型
bi = [0.0 for i in range(itemNum)]
bu = [0.0 for i in range(userNum)]
temp = math.sqrt(factorNum)
qi = [[(0.1 * random.random() / temp) for j in range(factorNum)] for i in range(itemNum)]	
pu = [[(0.1 * random.random() / temp)  for j in range(factorNum)] for i in range(userNum)]
print("initialization end\nstart training\n")

# 训练模型
s = []
rmse = []
preRmse = 1000000.0
iteration = 1000
for step in range(iteration):
	fi = open(trainDataFile, 'r')	
	for line in fi:
		arr = line.split()
		uid = int(arr[0].strip()) - 1
		iid = int(arr[1].strip()) - 1
		score = int(arr[2].strip())			
		prediction = PredictScore(averageScore, bu[uid], bi[iid], pu[uid], qi[iid])
			
		eui = score - prediction

		# 更新参数
		bu[uid] += learnRate * (eui - regularization * bu[uid])
		bi[iid] += learnRate * (eui - regularization * bi[iid])	
		for k in range(factorNum):
			temp = pu[uid][k]	#attention here, must save the value of pu before updating
			pu[uid][k] += learnRate * (eui * qi[iid][k] - regularization * pu[uid][k])
			qi[iid][k] += learnRate * (eui * temp - regularization * qi[iid][k])
	fi.close()
	learnRate *= 0.9
	curRmse = Validate(testDataFile, averageScore, bu, bi, pu, qi)
	print("test_RMSE in step %d: %f" %(step, curRmse))
	if curRmse >= preRmse:
		break
	else:
		preRmse = curRmse
	s.append(step)
	rmse.append(curRmse)
print(s)
print(rmse)
plt.plot(s, rmse)
plt.show()
return s, rmse

#验证模型
def Validate(testDataFile, av, bu, bi, pu, qi):
cnt = 0
rmse = 0.0
fi = open(testDataFile, ‘r’)
for line in fi:
cnt += 1
arr = line.split()
uid = int(arr[0].strip()) - 1
iid = int(arr[1].strip()) - 1
pScore = PredictScore(av, bu[uid], bi[iid], pu[uid], qi[iid])

	tScore = int(arr[2].strip())
	rmse += (tScore - pScore) * (tScore - pScore)
fi.close()
return math.sqrt(rmse / cnt)

if name == ‘main’:
configureFile = ‘svd.conf’
trainDataFile = ‘ml_data\training.txt’
testDataFile = ‘ml_data\test.txt’
modelSaveFile = ‘svd_model.pkl’
resultSaveFile = ‘prediction’

SVD(configureFile, testDataFile, trainDataFile, modelSaveFile)

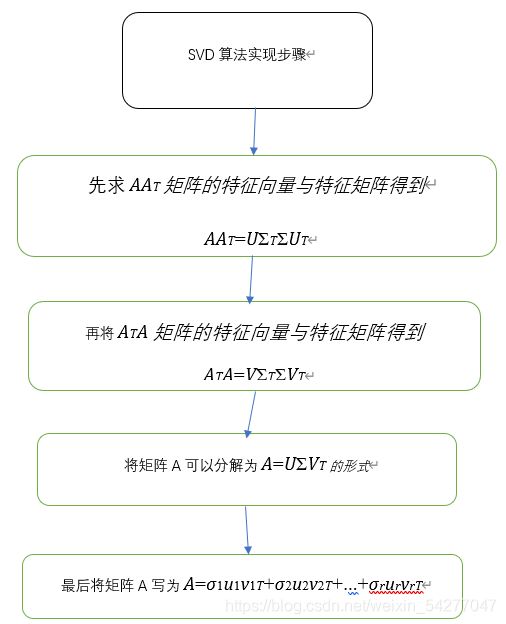
四、SVD算法的步骤和实现

A=UΣVT
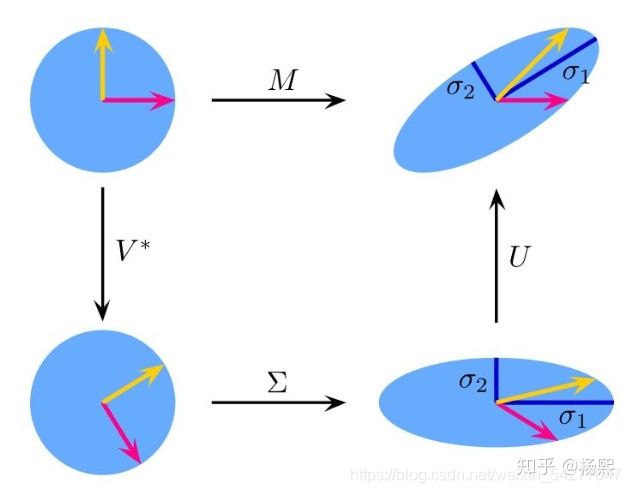
其中U是一个m×mm×m的矩阵，ΣΣ是一个m×nm×n的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，V是一个n×nn×n的矩阵。U和V都是酉矩阵，即满足UTU=I,VTV=IUTU=I,VTV=I。下图可以很形象的看出上面SVD的定义：

那么我们如何求出SVD分解后的U,Σ,VU,Σ,V这三个矩阵呢？
　　　　如果我们将A的转置和A做矩阵乘法，那么会得到n×nn×n的一个方阵ATAATA。既然ATAATA是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：
(ATA)vi=λivi(ATA)vi=λivi
　　　　这样我们就可以得到矩阵ATAATA的n个特征值和对应的n个特征向量vv了。将ATAATA的所有特征向量张成一个n×nn×n的矩阵V，就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。
　　　　如果我们将A和A的转置做矩阵乘法，那么会得到m×mm×m的一个方阵AATAAT。既然AATAAT是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：
(AAT)ui=λiui(AAT)ui=λiui
　　　　这样我们就可以得到矩阵AATAAT的m个特征值和对应的m个特征向量uu了。将AATAAT的所有特征向量张成一个m×mm×m的矩阵U，就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。
　　　　U和V我们都求出来了，现在就剩下奇异值矩阵ΣΣ没有求出了。由于ΣΣ除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值σσ就可以了。
　　　　我们注意到:
A=UΣVT⇒AV=UΣVTV⇒AV=UΣ⇒Avi=σiui⇒σi=Avi/uiA=UΣVT⇒AV=UΣVTV⇒AV=UΣ⇒Avi=σiui⇒σi=Avi/ui
　　　 这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵ΣΣ。
　　　 上面还有一个问题没有讲，就是我们说ATAATA的特征向量组成的就是我们SVD中的V矩阵，而AATAAT的特征向量组成的就是我们SVD中的U矩阵，这有什么根据吗？这个其实很容易证明，我们以V矩阵的证明为例。
A=UΣVT⇒AT=VΣTUT⇒ATA=VΣTUTUΣVT=VΣ2VTA=UΣVT⇒AT=VΣTUT⇒ATA=VΣTUTUΣVT=VΣ2VT
　　　　上式证明使用了:UTU=I,ΣTΣ=Σ2。UTU=I,ΣTΣ=Σ2。可以看出ATAATA的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到AATAAT的特征向量组成的就是我们SVD中的U矩阵。
　　　　进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：
σi=λi−−√σi=λi
　　　　这样也就是说，我们可以不用σi=Avi/uiσi=Avi/ui来计算奇异值，也可以通过求出ATAATA的特征值取平方根来求奇异值。
　　　　

五、SVD算法优点：

1）算法稳定；
2）适用面广；
3）简化数据，减小处理量；
4）去除噪声与冗余信息；
5）算法效果好。

六、建模实例

第五届MathorCup数学建模挑战赛D题：图像去噪中几类稀疏变换的矩阵表示
*

七、相关参数解释

1、特征值和特征向量
Ax=λxAx=λx
　　　　其中A是一个n×nn×n的实对称矩阵，xx是一个nn维向量，则我们说λλ是矩阵A的一个特征值，而xx是矩阵A的特征值λλ所对应的特征向量。

2、幺正矩阵、矩阵的相似对角化
参考线性代数第四章

八、小结

SVD作为一个很基本的算法，在很多机器学习算法中都有它的身影，特别是在现在的大数据时代，由于SVD可以实现并行化，因此更是大展身手。SVD的原理不难，只要有基本的线性代数知识就可以理解，实现也很简单因此值得仔细的研究。当然，SVD的缺点是分解出的矩阵解释性往往不强，有点黑盒子的味道，不过这不影响它的使用。

九、相关文献参考

https://zhuanlan.zhihu.com/p/79669616