论文笔记：NIPS 2019 Graph Transformer Networks
1. 前言
论文链接：https://arxiv.org/pdf/1911.06455.pdf
github：https://github.com/seongjunyun/Graph_Transformer_Networks
GNN 被广泛应用于图表示学习中，并且具有显著的优势。然而，大多数现有的 GNNs 被设计用于学习固定的同构图上的节点表示。在学习一个由各种类型的节点和边组成的异构图的表示时，这些限制尤其会成为问题。在本文中提出了能够生成新的图结构的图变网络(GTNs)，它包括识别原始图上未连接节点之间的有用连接，同时端到端的学习节点的有效表示。Graph Transformer Layer 是 GTNs 的核心层，它学习边缘类型和复合关系的软选择，从而生成有用的多跳连接，即所谓的元路径（meta-path）。
2. 背景
异质图在现实生活中被广泛的应用，例如，一个引文网络有多种类型的节点(如作者、论文、会议)和由它们之间的关系定义的边(如作者-论文、论文-会议)，它被称为异构图。一种简单的方法是忽略节点/边类型，并将它们视为同构图(具有一种节点和边类型的标准图)。这显然不是最优的，因为模型不能利用类型信息。利用传统的 GNN 方法可以处理异质图，处理的方式在于多种类型边的转换。这是一个两阶段的方法，需要为每个问题手工设计元路径。这些元路径的选择会显著影响下游分析的准确性。
本文提出的网络架构主要用于异质图网络的节点分类任务，传统的 GNN 方法包括 DeepWalk、LINE、node2vec等，这些方法过度依赖于图结构，同时没有很好的针对于下游任务进行优化。对于不久之前提出的 HAN 方法，作者认为是通过将异质图转换成多个同质图进行处理，其中对于元路径的选择需要手工操作这就可能导致信息的缺失。
因此作者提出了(GTN),与这些方法不同的是，GTN 可以在一个异构图上操作，并在以端到端方式学习转换图上的节点表示的同时转换任务。它可以学习将一个异构的输入图转换为对每个任务有用的元路径图，并以端到端方式学习图上的节点表示。将异构图转换为由元路径定义的新图结构的主要挑战是元路径可能具有任意长度和边的多种类型。
本文的贡献如下:
- (i)提出了一个新的图转换网络框架，以学习一种新的图结构，其中包括识别有用的元路径和多跳连接，以学习图上有效的节点表示。
- (ii)图的生成具有可解释性，模型能够洞察有效的元路径进行预测。
3. GTN
GTNs使用多个候选邻接矩阵寻找新的图结构，以执行更有效的图卷积，并学习更强大的节点表示。学习新的图结构包括识别有用的元路径，即连接异构边的路径和多跳连接。
作者提出异质图的邻接矩阵可以表达成多个邻接矩阵的形式，其中以每一条边的类型进行区分。符号表示为： { A k } k = 1 K ， K = ∣ T e ∣ ， A k ∈ R N × N \{A_k\}_{k=1}^K，K=|\mathcal{T}^e| ，A_k \in \mathbb{R}^{N \times N} {Ak}k=1K，K=∣Te∣，Ak∈RN×N。其中 T e \mathcal{T}^e Te 表示边的类型的集合，进而异质图的邻接矩阵可以写成 A ∈ R N × N × K \mathbb{A}\in\mathbb{R}^{N\times N\times K} A∈RN×N×K
其中还有结点的特征矩阵 X ∈ R N × D X \in \mathbb{R}^{N \times D} X∈RN×D
路径的概念包含了多跳连接，在 GTN 框架中新的图结构是由邻接矩阵表示的，举个例子，存在一条元路径 Author-Paper-Conference（APC）可以表示为 A → P → C A \rightarrow P \rightarrow C A→P→C，其中表达此关系的邻接矩阵 A A P C A_{APC} AAPC 可以有两个分别的邻接矩阵 A A P ， A P C A_{AP}，A_{PC} AAP，APC相乘得到。
由于 GTN 生成了全新的图结构，因此 GTN 框架从不同的卷积中受益，也就是说 D − 1 2 A D − 1 2 D^{-\frac{1}{2}}AD^{-\frac{1}{2}} D−21AD−21 中包含了学习到的多个邻接矩阵。
而对于有向图，正则化的形式可以变为 D − 1 D^{-1} D−1。因此对于有向图，最终的图卷积形式变为 H ( l + 1 ) = σ ( D ~ − 1 A H ( l ) W ( l ) ) H^{(l+1)}=\sigma(\widetilde{D}^{-1}AH^{(l)}W^{(l)}) H(l+1)=σ(D −1AH(l)W(l)).
3.1 Meta-Path Generation
之前的工作需要手工定义元路径，并在元路径图上塔尖图神经网络进行图卷积或者图注意力操作得到节点的表示。相反， GTN 为给定的数据和任务学习元路径，并在学习的元路径图上操作图卷积。这样就有机会找到更有用的元路径，并使用多个元路径图来实现各种各样的图形卷积。
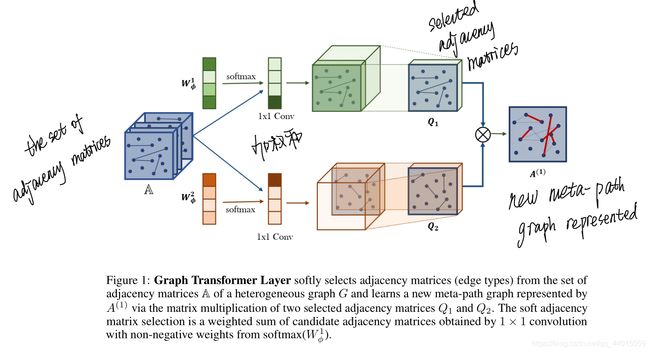
图1中的图Transformer (GT)层新生成的元路径图有两个组成部分。
首先，GT层从候选邻接矩阵 A \mathbb{A} A 中 softly selects 两个图结构 Q 1 Q_1 Q1 和 Q 2 Q_2 Q2。其次，它通过两个关系的组合(即两个邻接矩阵 Q 1 Q_1 Q1 和 Q 2 Q_2 Q2 的矩阵乘法)来学习新的图结构。邻接矩阵 Q Q Q 的选择方式如下：
其中 ϕ \phi ϕ 代表卷积层， W ϕ ∈ R 1 × 1 × K W_{\phi} \in \mathbb{R}^{1 \times 1 \times K} Wϕ∈R1×1×K 代表卷积层 ϕ \phi ϕ 的参数。 即得出的 Q Q Q 是将 A \mathbb{A} A 和权重参数 W ϕ W_{\phi} Wϕ 送去convolution layer卷积得到的
每一个 Q i Q_i Qi 可以表示成 ∑ t l ∈ T e α t l ( l ) A t l \sum_{t_l \in \mathcal{T}^e}\alpha_{t_l}^{(l)}A_{t_l} ∑tl∈Teαtl(l)Atl。其中 T e \mathcal{T}^e Te 是edge的类型集合， α t l ( l ) \alpha_{t_{l}}^{(l)} αtl(l) 是edge第 l l l 种类型 t l t_l tl 在第 l l l 层的权重。
以图中为例： T e \mathcal{T}^e Te 有4个 { t 1 , t 2 , t 3 , t 4 } \{t_1,t_2,t_3,t_4\} {t1,t2,t3,t4} 即对应4层matrices: { A 1 , A 2 , A 3 , A 4 } \{ A_1,A_2,A_3,A_4\} {A1,A2,A3,A4} ， W ϕ = { α 1 , α 2 , α 3 , α 4 } W_{\phi}=\{α_1,α_2,α_3,α_4\} Wϕ={α1,α2,α3,α4}
如果不是分两个Q，而是多个，则最后得到的结果新A可表示为：
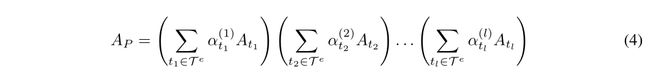
其中 A p A_p Ap 代表了元路径的邻接矩阵，可以看作是所有长度为 l l l 元路径邻接矩阵的加权和。因此，一个l个 GT 层的堆栈可以学习任意长度的 l l l 元路径图结构。
这种结构的一个问题是，添加GT层总是会增加元路径的长度，而不允许使用原始的边。在一些应用中，长元路径和短元路径都很重要。为了学习包含原始边的短元路径和长元路径（如果全部按照图中的生成，则每一条元路径都是基于原始边所生成的，也就忽略了原始边的本身的特征），本文中包括了单位矩阵以学习原始边的数据特征。即 A 0 = I A_0=I A0=I。这个技巧可以让 GTN 网络学习任意长度的元路径
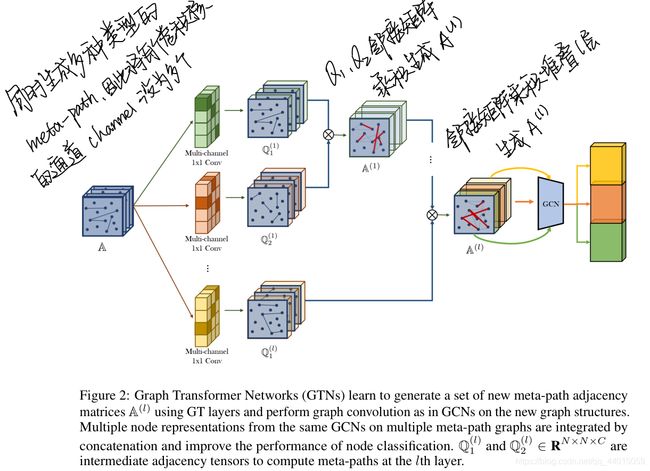
3.2 Graph Transformer Networks
这属于上面介绍结构的变体，为了同时生成多种类型的元路径，图1中1×1卷积的输出通道设置为C。
4. 实验
