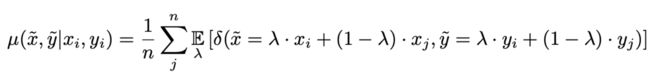mixup
正则化:数据增强—mixup
论文链接:mixup: BEYOND EMPIRICAL RISK MINIMIZATION(ICLR-2018)
mixup的基本原理
通过构建数据对之间的线性组合,构建了经验分布的近邻分布,从而减小经验风险损失。
mixup提出的理论推导过程
经验分布 P δ P_\delta Pδ只是众多近似真实分布 P P P的一种分布,根据VRM(Vicinal Risk Minimization (VRM) principle ),可以通过高斯分布等方法去找到当前 P δ P_\delta Pδ的近邻分布 P v P_v Pv,从而尽可能减小经验风险损失。
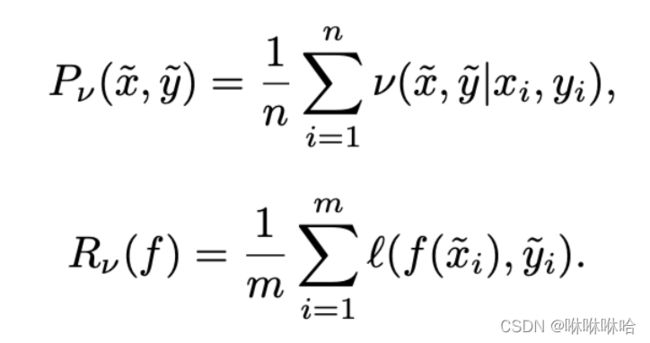
论文提出的mixup也是一种构建 P v P_v Pv的方法。
其中 λ ∼ B e t a ( α , α ) , α ∈ ( 0 , + ∞ ) \lambda \sim Beta(\alpha,\alpha), \alpha \in (0, +\infty) λ∼Beta(α,α),α∈(0,+∞),那么可以知道 λ ∈ [ 0 , 1 ] \lambda \in [0,1] λ∈[0,1] 。
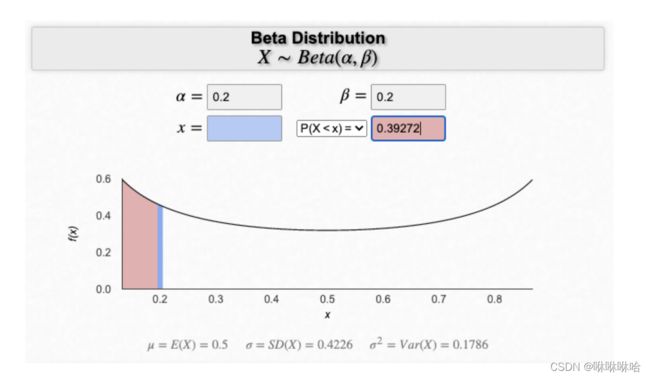
为什么选择Beta分布呢?答案是比较明显的,
一个直观的理解是,mixup是对一个pair进行的操作,在没有特殊条件限制或不同采样规则的前提下,一个pair的两个sample应该是等价的,所以采样需要在0-1之间并关于0.5对称,而 B e t a ( α , α ) Beta(\alpha,\alpha) Beta(α,α)正好符合这个特点。
这是我发现的一个展示Beta分布的网页,有助于直观感受一下参数 α \alpha α对Beta分布曲线的影响
这里的 α \alpha α是一个超参数,如何设置比较合适呢?我们来看一下实验部分的结果。
CV相关的实验结果总结
1、在cifar-10,cifar-100数据集上,可以观测到当 α ∈ [ 0.1 , 0.4 ] \alpha \in [0.1, 0.4] α∈[0.1,0.4],效果比较好,过大的 α \alpha α会带来过拟合问题。
2、通过设置 α = 1 \alpha=1 α=1,也就是 λ \lambda λ在[0,1]上均匀采样,对比了mixup和ERM多组实验结果,发现两者具有相同的收敛速度,基本上在相同的时间内达到了各自的最好的测试集错误率。
代码实现
论文给出了pytorch版本的单个数据上的实现方式:
我的代码实现
对于batch data,我的实现方式如下:
def mixup(x: torch.Tensor, y: torch.Tensor, alpha: float = 1.0):
assert alpha > 0, "alpha should be larger than 0"
assert x.size(0) > 1, "Mixup cannot be applied to a single instance."
lam = np.random.beta(alpha, alpha)
rand_index = torch.randperm(x.size()[0])
mixed_x = lam * x + (1 - lam) * x[rand_index, :]
target_a, target_b = y, y[rand_index]
return mixed_x, target_a, target_b, lam
计算损失的时候,也要做对应的修改:
# 对应的损失函数for batch data
mix_inputs, target_a, target_b, lam = mixup(inputs, train_labels, alpha=0.2)
outputs = model(mix_inputs)
loss = loss_function(outputs, target_a) * lam + \
(1 - lam) * loss_function(outputs, target_b)
我在自己比较小的一个医学影像数据集上使用mixup,确实能有效防止模型过拟合,减少模型对数据的记忆。
参考链接
https://www.zhihu.com/question/435426841
https://www.jianshu.com/p/ac23eec2d054