可解释人工智能——输入单元重要性归因

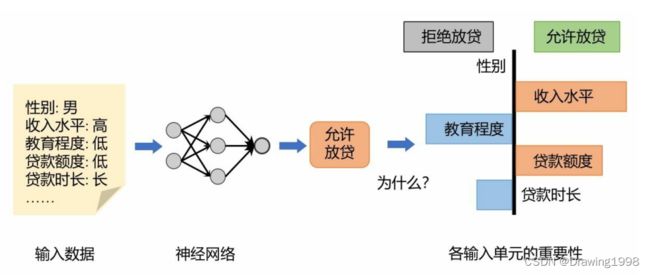
输入单元重要性归因，即计算输入中各个单元的重要性（Importance）。重要性能够反映该输入单元对于神经网络的影响大小，重要性越高，表明影响越大。为输入单元的重要性进行量化和分析，能够帮助人们理解是哪些输入变量促使神经网络得到了当前的结果，从而对神经网络的特征建模有一个初步的认识。

在某些研究中，人们会使用归因值（Attribution）或显著性（Saliency）描述某个输入单元对神经网络的影响，而重要性、归因值和显著性的含义非常相似。因此在下面的讨论中将统一采用重要性这一说法。

最具代表性的可解释性方法：

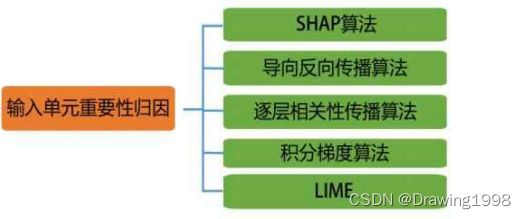
1. SHAP算法

1.1 Shapley Value

Shapley Value是联盟博弈论（cooperative game theory）的一种方法，是一种根据 玩家(特征) 对 总支出(预测) 的贡献 来给玩家分配总支出的方法。玩家在联盟中进行合作，并从合作中获得一定的收益。

Shapley Value 是对所有可能联盟(coalition) 的 所有边际贡献的 平均值。可以这样来直观理解Shapley Value：特征值以随机顺序进入房间，房间中的所有特征值都参与游戏（相当于有助于预测）。特征值的 Shapley值是当该特征值加入它们时，已经存在于房间中的联盟所收到的预测值的平均变化。

例如：三个玩家合作完成一个项目（制作500个零件）。
每个玩家可以独立制作的零件数量：v({1})=100，v({2})=125，v({3})=50；
如果合作：v({1,2})=270，v({1,3})=375，v({2,1})=270，v({2,3})=350，v({3,1})=375，v({3,2})=350，v({1,2,3})=500
则在{1,2}的合作中，玩家2的边际贡献=v({1,2})-v({1})=270-100=175
在{1,2,3}的合作中，玩家3的边际贡献=v({1,2,3})-v({1,2})=500-270=230

概率	玩家加入顺序	玩家1的边际贡献	玩家2的边际贡献	玩家3的边际贡献
$\frac{1}{6}$	1,2,3	100	170	230
$\frac{1}{6}$	1,3,2	100	125	275
$\frac{1}{6}$	2,1,3	145	125	230
$\frac{1}{6}$	2,3,1	150	125	225
$\frac{1}{6}$	3,1,2	325	125	50
$\frac{1}{6}$	3,2,1	150	300	50

那么，每个玩家的Shapley Value为：

玩家	Shapley Value
1	$\frac{1}{6}(100+100+145+150+325+150)=\frac{970}{6}$
2	$\frac{1}{6}(170+125+125+125+125+300)=\frac{970}{6}$
3	$\frac{1}{6}(230+275+230+225+50+50)=\frac{1060}{6}$

因此，按照比例来分奖金的话，玩家1分配的奖金为总奖金的32.3%，玩家2分配的奖金为总奖金的32.3%，玩家3分配的奖金为总奖金的35.3% 。

那么在机器学习中，我们怎么控制某一个玩家(特征) 有没有 参与游戏呢？
如果某个玩家不参与游戏的话，我们就给这个特征一个随机值，这个随机值来自 训练数据集中特征的分布。被赋予随机值的特征是没有预测能力的，这样的话我们就认为该特征没有参与游戏(预测)。


Shapley Value 存在的缺陷：

• 时间复杂度太高
• Shapley Value 为每个特征返回一个简单值，但没有像 LIME 这样的模型。这意味着它不能用于对 输入变化的预测 做出 变化的陈述。
• 如果要计算新数据实例的Shapley值，需要访问很多数据来进行计算。
• 与很多其他基于置换的解释方法一样，Shapley值方法在特征相关的情况下，会遇到不符合实际的数据实例。

1.2 SHAP算法

考虑到Shapley Value的计算需要非常高的计算复杂度，2017年，Lundberg与Lee提出了Shapley可加性解释（SHapley Additive exPlanations, SHAP）算法${}^{[2]}$，对输入单元的Shapley Value进行高效近似，目标是通过计算每个特征对预测的贡献来解释实例$x$的预测。将模型的预测值解释为二元变量的线性函数：
$$g(z^{\prime })={\varphi }_0+\sum _{i=1}^M{\varphi }_i{z}_i^{\prime }$$其中，$g$是解释模型；$z^{\prime }\in \{0,1{\}}^M$ 是联盟向量（也称“简化特征”，1-present, 0-obsent）；$M$是最大联盟的大小；${\varphi }_i\in R$是特征$i$的特征归因Shapley值。

SHAP描述了以下三个理想的性质：

• 局部准确度（Local Accuracy）：特征归因的总和等于要解释的模型的输出。即 $f(x)=g(x^{\prime })={\varphi }_0+\sum _{i=1}^M{\varphi }_i{x}_i^{\prime }$
• 缺失性（Missingness）：要解释的实例的所有特征值$x_i^{\prime }$均应为“1”，如果为“0”则表示要解释的实例缺少这个特征值。
• 一致性（Consistency）：如果模型发生变化使得特征值的边际贡献增加或保持不变（不考虑其他特征），则Shapley值也会相应地增加或保持不变。

计算重要性：

• KernelSHAP${}^{[2]}$：KernelSHAP是一种基于核的代理方法，根据局部代理模型对Shapley values进行估算。
• DeepSHAP${}^{[3]}$：通过对此前的一些基于反向传播的算法（DeepLIFT${}^{[4]}$）进行改良，得到了DeepSHAP。
  
  

1. KernelSHAP（Linear LIME + Shapley values）

（1）KernelSHAP 简介

KernelSHAP为一个实例$x$估算每个特征值对预测的贡献。

回想一下SHAP：SHAP 将解释定义为：$g(z^{\prime })={\varphi }_0+\sum _{j=1}^M{\varphi }_j{z}_j^{\prime }=f(z)$ ，即SHAP想要训练一个回归模型来在局部拟合要解释的模型输出。（等等，这不是LIME模型要做的事吗？！）在这里我们想要看到每个特征对应的Shapley值（每个特征对预测的贡献），即 ${\varphi }_j$ 。

KernelSHAP 与 LIME 最大的不同就在于 回归模型中实例的权重。

• LIME 根据实例与原始实例的接近程度对其进行加权；

• SHAP 根据联盟在 Shapley值估计中 获得的权重 对采样实例进行加权。

  为了达到 Shapley标准 的加权，Lundberg 等提出了 SHAP核：（${\pi }_x(z^{\prime })$ 即表示 实例$z^{\prime }$ 对应的权重）

  $${\pi }_x(z^{\prime })=\frac{(M-1)}{(\begin{array}{c}M\\ |z^{\prime }|\end{array})|z^{\prime }|(M-|z^{\prime }|)}$$其中，$M$是最大联盟大小；$|z^{\prime }|$ 是实例 $z^{\prime }$ 中当前特征的数量。

（2）KernelSHAP 是怎样进行计算的？

KernelSHAP 的计算主要包含以下5个步骤：${}^{[10]}$

1. 在目标实例附近初始化一些 simplified features $z_k^{\prime }\in \{0,1{\}}^M$ （1表示联盟中存在特征，0表示联盟中不存在特征）。
2. 将 simplified features $z_k^{\prime }$ 转换到原始数据空间 $h_x(z^{\prime })=z$，然后应用模型 $f:f(h_x(z_k^{\prime }))$ 对 $z_k^{\prime }$ 进行预测。
   这里如果vector为1，则使用该feature的原始数据；如果vector为0，即意味着“缺少特征值”，此时 $h_x$ 会根据当前特征值对不存在的特征值从边际分布进行采样（从边际分布进行采样意味着忽略当前特征和不存在特征之间的依赖关系）。
3. 使用SHAP核计算每个 $z_k^{\prime }$ 的权重。
   $${\pi }_x(z^{\prime })=\frac{(M-1)}{(\begin{array}{c}M\\ |z^{\prime }|\end{array})|z^{\prime }|(M-|z^{\prime }|)}$$
4. 拟合加权线性模型。
5. 返回 Shapley Value ${\varphi }_k$ ，即线性模型的系数。

2. DeepSHAP（DeepLIFT + Shapley values）

DeepSHAP 使用 DeepLIFT方法来估算每个特征对应的 Shapley Value。

2. LIME 局部与模型无关解释方法

2.1 LIME简介

LIME${}^{[9]}$全称是：Local Interpretable Model-agnostic Explanations，局部代理模型（即 专注于训练局部代理模型以解释单个预测）。local - 局部（样本空间的局部），model-agnostic - 与模型无关。

这种方法把原始模型看作一个黑盒子，可以在其中输入数据点并获得模型的预测。可以随时探测黑盒，LIME模型的目标是 了解该黑盒模型为何做出特定的预测。

LIME生成一个新的数据集，然后在这个新的数据集上，LIME训练了一个 可解释的模型（例如，线性模型、决策树 等），该模型根据新样本 与 目标实例 的接近度（可以理解为是距离）(Proximity) 进行加权。所学习的模型应该是 机器学习模型 局部预测 的良好近似，但不一定是良好的全局近似。

在数学上，具有可解释性约束的 局部代理模型可以表示为：

$explanation(x)=argmi{n}_{g\in G}L(f,g,{\pi }_x)+\Omega (g)$

式中，$g$ 是对 $x$ 的解释模型，$f$ 表示原始模型，最小化损失 $L$ 测量了 解释模型 $g$ 与 原始模型 $f$ 的预测的接近程度，接近度 ${\pi }_x$ 定义了 考虑解释时 实例 $x$ 附近的邻域大小，模型复杂度 $\Omega (g)$ 保持较低水平（例如：对于决策树，$\Omega (g)$ 可能是树的深度）。在实际运算过程中，LIME 仅优化损失部分，用户必须确定复杂度。

2.2 LIME是怎样进行计算的？

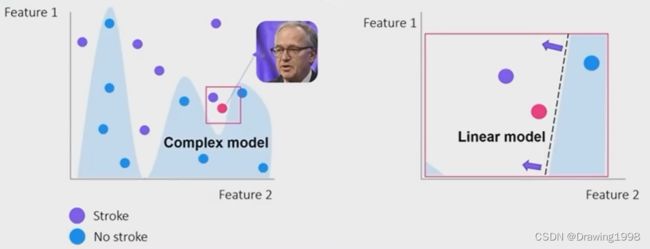
左边是一个用来解决分类问题的复杂模型，针对某一个样本，我们想知道是哪些因子影响了该样本的分类。
我们把这个局部区域取出来，用一个线性模型来拟合决策边界。我们是怎么做的呢？

1. 在预测样本附近生成很多样本点。针对这个样本点，我们在它的周围随机生成很多样本点。
   
2. 对新生成的样本打标签。我们将新生成的样本放入已经训练好的复杂模型 $f$ 中进行预测，得到对应的预测结果。
3. 用打好标签的样本来训练解释模型 g。找到使加权损失 $L(f,g,{\pi }_x)$ 最小的 解释模型 g。为什么是加权损失呢？因为我们新生成的样本点距离 预测样本 有近有远，这些样本点不能一视同仁，距离 预测样本 大一些的样本点权重大些，距离远的样本点权重小些。
   
   
   

2.3 LIME算法是怎么做解释的？

通过上面的介绍我们知道LIME训练了一个可解释模型（线性模型、决策树等），该模型是 针对目标实例 与原机器学习模型的局部良好近似。训练得到的可解释模型为每个输入单元分配的权重，即为这些输入单元的重要性。

3. 基于反向传播来计算梯度的可解释性方法

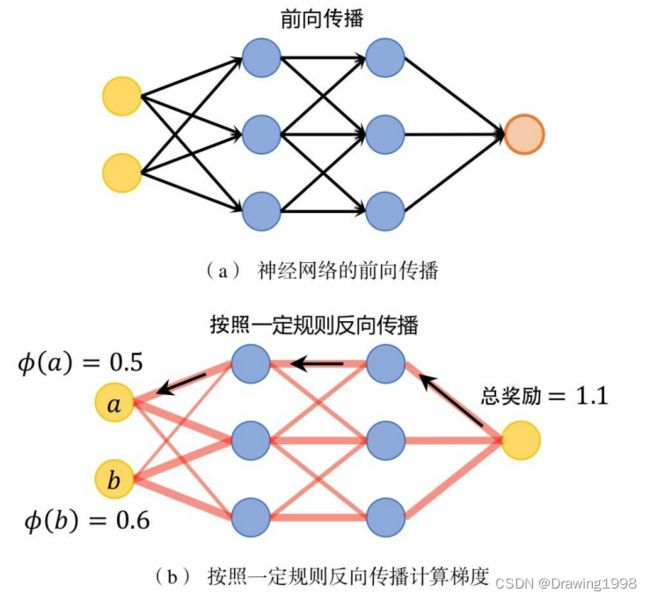
在可解释性方法中，有一大类方法基于反向传播，计算各个输入单元的梯度，并且将梯度作为该输入单元的重要性。如下图所示，基于反向传播的可解释性方法会为神经网络中的卷积层、池化层、非线性激活层等每层设计反向传播的规则，使得其在反向传播的过程中，能够更为公平合理地分配重要性的数值，最终为各个输入单元求得的梯度值能够很好地反映这一输入单元的重要程度。

3.1 GBP 导向反向传播算法

这里我们需要理解 反卷积(deconvnet) 、反向传播(backpropagation) 和 导向反向传播(guided backpropagation) 三个概念。

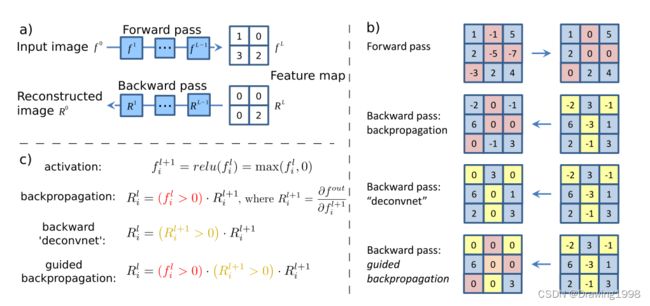
1. 反卷积(Deconvnet)

在Visualizing and Understanding Convolutional Networks这篇论文中，反卷积（deconvnet）被用来对CNN的中间层进行可视化。一般的卷积神经网络的基本构成块是卷积层 + ReLU激活函数 + 最大池化，deconvnet就是执行这三个过程的逆向操作，即反最大池化 + 反ReLU + 反卷积操作。详见这篇文章。

2. 反向传播(backpropagation)

参考文章1
参考文章2

3. 导向反向传播(Guided BackPropagation)

在导向反向传播（Guided-Backpropagation, GBP）算法${}^{[5]}$ 中，除ReLU层之外的其他层，包括卷积层、池化层等，在反向传播时都会采用传统的反向传播计算规则。而对于ReLU层，GBP算法会将小于0的梯度值置为0，然后再继续进行梯度的传播，并将最终每个输入样本得到的梯度作为其重要性的解释结果。

GBP算法相当于对普通的反向传播加了指导，限制了小于0的梯度的回传，而梯度小于0的部分对应了原图中削弱了我们想要可视化的特征的部分，这些部分正是我们不想要的。

在这张图中，

• 图a表示给定一个输入图像，我们对感兴趣的层执行前向传播，然后将除一个激活外的所有激活设置为零，并进行反向传播以重建原始图像；
• 图b表示通过ReLU非线性反向传播的不同方法；
• 图c正式定义输出激活通过l层的ReLU单元向外传播的不同方法，注意：deconvnet 和 guided backpropagation 计算的不是真正的梯度，而是梯度的估算版本。

3.2 Integral Gradient 积分梯度算法

基于反向传播来计算梯度的可解释性方法很直观，可以利用为各个输入单元求得的梯度值来表征这一输入单元的重要程度。但是该方法存在的局限性在于Gradient Saturation（梯度饱和）问题，即加入某个因素对图片的预测起到了推进作用，但是这个作用是有限的，超过了一定程度后就不再增加预测的几率了，此时在超过这个程度之后的地段会出现梯度为0的情况。 梯度为0时就揭示不出什么有效信息了。如下图：

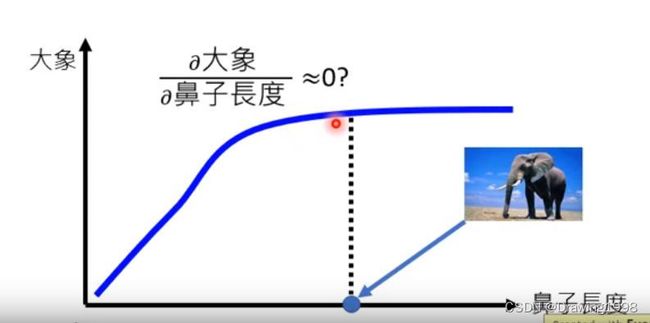
针对 Gradient-based 方法存在的缺陷，2017年 Sundararajan等人提出了积分梯度（IntegralGradient, IG）算法${}^{[8]}$。该方法对各输入变量的梯度值进行积分，以此来表征输入变量的重要程度。即：

3.3 LRP 逐层相关性传播算法

逐层相关性传播（Layer-wise Relevance Propagation, LRP）算法假设神经网络各层的神经元与神经网络的输出之间存在一定的相关性（Relevance），相关性越大的神经元对于神经网络的输出影响越大，重要性也就越高。

还没完全看明白，感觉有点像LSTM的门控机制，选择性的保留上一层神经元的内容。

---

参考：
[1] 可解释人工智能导论
[2] Lundberg S M, Lee S I. A unified approach to interpreting model predictions[J]. Advances in neural information processing systems, 2017, 30.
[3] Fernando Z T, Singh J, Anand A. A study on the Interpretability of Neural Retrieval Models using DeepSHAP[C]//Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval. 2019: 1005-1008.
[4] Shrikumar A, Greenside P, Kundaje A. Learning important features through propagating activation differences[C]//International conference on machine learning. PMLR, 2017: 3145-3153.
[5] Springenberg J T, Dosovitskiy A, Brox T, et al. Striving for simplicity: The all convolutional net[J]. arXiv preprint arXiv:1412.6806, 2014.
[6] “直观理解”卷积神经网络(二)：导向反向传播(Guided-Backpropagation)
[7] 直观理解深度学习中的反卷积、导向反向传播
[8] Sundararajan M, Taly A, Yan Q. Axiomatic attribution for deep networks[C]//International conference on machine learning. PMLR, 2017: 3319-3328.
[9] Ribeiro M T, Singh S, Guestrin C. " Why should i trust you?" Explaining the predictions of any classifier[C]//Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. 2016: 1135-1144.
[10] KernelSHAP & TreeSHAP