【读论文】A Unified Approach to Interpreting Model Predictions

1. 这篇文章主要做了什么？

文章提出了一个解释预测的统一框架SHAP（SHapley Addictive exPlanations），SHAP为每个特征指定一个特定预测的重要值。

引入了将模型预测的任何解释视为模型本身的观点，我们称之为解释模型。这让我们可以定义加性特征归因方法的类，它统一了目前的六种方法。并提出将SHAP值作为各种方法近似的特征重要性的统一度量。

2. Additive Feature Attribution Methods 加性特征归因方法

对简单模型最好的解释就是模型本身，它完美地代表了自己，很容易理解。对于复杂的模型，如深度网络，我们不能用原始模型作为它自己的最佳解释，因为它不容易理解，相反，我们必须使用一个更简单的解释模型，将其定义为原始模型的任何可解释近似。

设$f$为待解释的原始预测模型，$g$为解释模型。在这里我们着重于用于解释基于单个输入$x$的预测$f(x)$的局部方法。
如LIME${}^{[1]}$中所提出的：解释模型通常使用简化的输入$x^{\prime }$ ，通过映射函数 $x=h_x(x^{\prime })$映射到原始输入，当 $x^{\prime }\approx z^{\prime }$ 时，局部方法试图确保 $g(z^{\prime })\approx f(h_x(z^{\prime }))$ 。

定义1：加性特征归因方法的解释模型是二元变量的线性函数：
$$g(z^{\prime })={\varphi }_0+\sum _{i=1}^M{\varphi }_i{z}_i^{\prime }$$其中，$z^{\prime }\in \{0,1{\}}^M$ ，$M$是简化输入特征的数量。

解释模型为每个特征$x_i$计算一个贡献度${\varphi }_i$，所有特征属性的贡献度之和 近似于 原始模型的输出$f(x)$ 。

下面介绍六种已有的解释方法，SHAP将这六种方法进行了统一。

2.1 LIME

LIME方法基于对模型给定预测的局部逼近来解释单个模型的预测

2.2 DeepLIFT

2.3 Layer-Wise Relevance Propagation

2.4 Classic Shapley Value Estimation

2.4.1 Shapley Regression Values

2.4.2 Shapley Sampling Values

2.4.3 Quantitative Input Influence

3. SHAP的性质

1. 局部准确度（Local Accuracy）

$$f(x)=g(x^{\prime })={\varphi }_0+\sum _{j=1}^M{\varphi }_j{x}_j^{\prime }$$特征归因的总和 等于 要解释的模型的输出。

2. 缺失性（Missingness）

$$x_j^{\prime }=0\Rightarrow {\varphi }_j=0$$缺失性表示 缺失特征的归因为零。

在联盟表示法中，要解释的实例的所有特征值 $x_j^{\prime }$ 均应为“1”。如为0，则意味着感兴趣的实例缺少这个特征值。

3. 一致性（Consistency）

令 $f_x(z^{\prime })=f(h_x(z^{\prime }))$ 且 $z_{\setminus j}^{\prime }$ 表示 $z_j^{\prime }=0$ 。对于任意两个模型 $f$ 和 $f^{\prime }$ 满足：对于所有的输入 $z^{\prime }\in \{0,1{\}}^M$ ，若：
$$f_x^{\prime }(z^{\prime })-f_x^{\prime }(z_{\setminus j}^{\prime })\ge f_x(z^{\prime })-f_x(z_{\setminus j}^{\prime })$$则有：
$${\varphi }_j(f^{\prime },x)\ge {\varphi }_j(f,x)$$一致性表示，如果模型发生变化使得特征值的边际贡献 $f_x(z^{\prime })-f_x(z_{\setminus j}^{\prime })$ 增加或保持不变（不考虑其他特征），则Shapley值也会增加或保持不变。

定理1：只有一个可能的解释模型 $g$ 符合 定义1 并满足上述3个性质。（即Shapley值计算公式，在所有可能的特征值组合上加权求和）
$${\varphi }_i(f,x)=\sum _{z^{\prime }\subseteq x^{\prime }}\frac{|z^{\prime }|!(M-|z^{\prime }|-1)!}{M!}[f_x(z^{\prime })-f_x(z^{\prime }\setminus i)]$$其中，$z^{\prime }$ 是模型中使用的特征的子集，$|z^{\prime }|$ 是 $z^{\prime }$ 中非零项的个数。

我对这个公式的理解：

---

首先先介绍一下Shapley value的计算过程：（参考自Shapley Values : Data Science Concepts）
原始样本：（其中T是我们感兴趣的特征，即下面展示的是只计算特征T的shapley value的过程）

T	D	F	H
80	1	100	4

• step 1 ：将特征进行随机排列。[T , D , F , H] -> [F , D , T , H]
• step 2 ：从数据集中随机挑选一个样本。

  	F	D	T	H
  original sample	100	1	80	4
  random sample	200	5	70	8

• step 3 ：构造 x1 & x2
  x1 = [100 , 1 , 80 , 8]
  x2 = [100 , 1 , 70 , 8]
  可以看出我们感兴趣的特征T左边的特征值来自original sample，T右边的特征值来自random sample。x1和x2的不同之处在于x1中T的特征值来自original sample，x2中T的特征值来自random sample。
  
  我们这样构造向量在一定程度上减轻了部分依赖图(Partial Dependence Plot , PDP)中的 isolated effect。因为独立性假设是部分依赖图最大的问题，即假定了计算部分依赖图的特征与其他特征不相关，当特征关联时，这种方式可能会在特征分布区域构造出实际概率非常低的样本点。（解决这个问题的一种方法是适用于条件分布而非边际分布的累积局部效应图（Accumulated Local Effect , ALE））
  （部分依赖图是对边际效应求平均值；累积局部效应图是对特征的条件分布求平均值。）
  （虽然Shapley value这样构造向量在一定程度上减轻了 isolated effect，但在特征相关的情况下，该方法还是会出现构造出不符合实际的样本的情况。）
  
  用原始复杂模型对我们构造的样本x1和x2进行预测：
  f(x1) = 1500 , f(x2) = 1400
  DIFF = f(x1) - f(x2) = 100 (This is the effect from T=80)
  
  
• step 4 ：记录每一次计算得到的DIFF，重复 step1 ~ step3 。对计算得到的所有DIFF求和取平均。

---

在每一轮step1~step3的过程中，令特征T左边的特征集合为 $z^{\prime }$ ，则特征T右边的特征集合为 $x^{\prime }-T-z^{\prime }$ 。集合 $z^{\prime }$ 有 $|z^{\prime }|!$ 种排列方式，集合 $x^{\prime }-T-z^{\prime }$ 有 $(M-|z^{\prime }|-1)!$ 种排列方式。因此在每一轮中共有 $[|z^{\prime }|!(M-|z^{\prime }|-1)!]\cdot [f_x(z^{\prime })-f_x(z^{\prime }\setminus i)]$ 种情况。

对所有的情况进行求和：
$$\sum _{z^{\prime }\subseteq x^{\prime }}[|z^{\prime }|!(M-|z^{\prime }|-1)!]\cdot [f_x(z^{\prime })-f_x(z^{\prime }\setminus i)]$$
再取平均即得到样本 $xx$ 中特征T 在模型 $f$ 的预测中的 贡献度（Shapley值）：
$$\begin{gathered} {\varphi }_T=\frac{1}{M}\sum _{z^{\prime }\subseteq x^{\prime }}[|z^{\prime }|!(M-|z^{\prime }|-1)!]\cdot [f_x(z^{\prime })-f_x(z^{\prime }\setminus i)] \\ =\sum _{z^{\prime }\subseteq x^{\prime }}\frac{|z^{\prime }|!(M-|z^{\prime }|-1)!}{M!}[f_x(z^{\prime })-f_x(z^{\prime }\setminus i)] \end{gathered}$$

4. SHAP（SHapley Additive exPlanation）Values

SHAP为一个实例$xx$估算每个特征值对预测的贡献。

SHAP值提供了唯一的附加特征重要性度量，它遵循属性1~3，并使用条件期望定义简化输入。在这个SHAP值的定义中隐含着一个简化的输入映射$h_x(z^{\prime })=z_S$，其中$z_S$包含了集合$S$之外的特征缺失值。由于大多数模型不能处理缺少输入值的任意模式，因此我们用 $E[f(z)|z_S]$ 来近似 $f(z_S)$ 。

SHAP 的精确计算是具有挑战性的，但我们可以通过结合当前的附加特征归因方法来对Shapley value进行近似。下面介绍了几种对Shapley value进行近似的方法：

注：在使用这些方法时，特征独立性 和 模型线性 是两个可选的假设，简化了期望值的计算。（不太懂）

4.1 Model-Agnostic Approximation Methods 与模型无关的近似方法

1. Shapley Sampling Values（already known）

如果我们在逼近条件期望时假设特征独立性，那么可以直接使用 Shapley Sampling Values${}^{[2]}$ 方法或等效的 Quantitative Input Influence${}^{[3]}$ 方法 来估计SHAP值。这些方法使用经典的Shapley值方程的置换版本来进行近似。

精确的 Shapley 值必须通过使用第 $j$ 个特征和不适用第 $j$ 个特征的所有可能的联盟（集合）来估计。当特征比较多时，随着更多特征的添加，可能的联盟数量呈指数级增长，使得计算其精确解成为问题。Štrumbelj 等人${}^{[2]}$提出了蒙特卡洛抽样的近似值：
$${\varphi }_j=\frac{1}{M}\sum _{m=1}^M(f(x_{+j}^m)-f(x_{-j}^m))$$其中，

• $M$ 为迭代次数，$xx$ 为感兴趣的样本，$j$ 为感兴趣的特征；
• $x_{+j}^m$ 表示除了特征 $j$ 的值，其他不在联盟内的特征值均被来自随机数据点 $z$ 的特征值替换；
• $x_{-j}^m$ 与 $x_{+j}^m$ 类似，但用来自随机数据点 $z$ 的特征值替换的特征 包括特征 $j$。
  （所以 $x_{+j}^m$ 和 $x_{-j}^m$ 唯一的不同就是特征 $j$ 的值不同。）

示例：（参考自Shapley Values : Data Science Concepts）

• 样本 $xx$ 有 [F , D , T , H] 4个特征，特征值为：[100 , 1 , 80 , 4] ，其中 T 是我们感兴趣的特征。
  我们将不在联盟内的特征值放在 T 的右边，这些特征值是变量(variable)。这里不在联盟内的的特征是H。
• 然后从数据集中随机选择一个样本，例如 [200 , 5 , 70 , 8]
• Form vectors $x_{+j}$ & $x_{-j}$ ：
  • $x_{+j}$ = [100 , 1 , 80 , 8]
  • $x_{-j}$ = [100 , 1 , 70 , 8]

2. Kernel SHAP（novel）

部分内容参考自：
[1]《Interpretable Machine Learning : A Guide for Making Black Box Models Interpretable》
[2] Shapley与SHAP

Kernel SHAP 可以理解为是 Linear LIME + Shapley values 。该方法是一种基于核的代理方法，可根据局部代理模型对 Shapley值 进行估算。

Kernel SHAP 是 model-agnostic 的，即可以应用于任何模型。

回顾：SHAP将 Shapley值 的解释表示为一种可加的特征归因方法，即线性模型。将解释模型定义为：
$$g(z^{\prime })={\varphi }_0+\sum _{i=1}^M{\varphi }_i{z}_i^{\prime }$$其中，$z^{\prime }\in \{0,1{\}}^M$ ，$M$是简化输入特征的数量（最大联盟的大小），${\varphi }_j$ 是特征 $j$ 的特征归因 Shapley值。

那么问题来了：怎样利用 Linear LIME 来近似得到 Shapley值呢？
答案取决于损失函数$L$ ，加权核${\pi }_{x^{\prime }}$ 和 正则化项 $\Omega$ 的选择。

定理2：Shapley Kernel ：

其中，$|z^{\prime }|$ 是 $z^{\prime }$ 中非零项的个数。
可以看出，Kernel SHAP 与 LIME 的最大区别就在于回归模型中实例的权重。LIME 根据实例与原始实例的接近程度对其进行加权；Kernel SHAP 根据联盟在 Shapley 值估计中获得的权重对采样实例进行加权。



Kernel SHAP 包含5个步骤：

1. 采样联盟 $z_k^{\prime }\in \{0,1{\}}^M,k\in \{1,2,...,K\}$ （1表示联盟中存在特征，0表示不存在特征）；

2. 对 $z_k^{\prime }$ 预测，方法是首先将 $z_k^{\prime }$ 转换为原始特征空间，然后应用模型 $f:f(h_x(z_k^{\prime }))$ ；
   

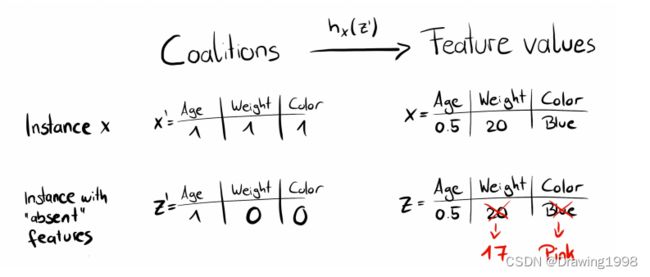
3. 使用SHAP kernel计算每个 $z_k^{\prime }$ 的权重；

4. 拟合加权线性模型；

5. 返回 Shapley值 ${\varphi }_k$ ，即线性模型的系数。

为什么这样的线性模型拟合出来的每个特征的权重就是Shaple value呢？
参考原文：The intuitive connection between linear regression and Shapley values is that Equation 8 [Sahpley计算公式] is a difference of means. Since the mean is also the best least squares point estimate for a set of data points, it is natural to search for a weighting kernel that causes linear least squares regression to recapitulate the Shapley values. This leads to a kernel that distinctly differs from previous heuristically chosen kernels (Figure 2A).
线性回归和Shapley值之间的直观联系是：Shapley值计算公式是 差值取平均。由于平均值也是一组数据点的最佳最小二乘点估计，因此我们想要找到一个加权核，该加权核能够导致最小二乘回归，以再现Shapley值。
最小二乘的思想就是要使得观测点和预测点之间的距离达到最小。

4.2 Model-Type-Specific Approximation Methods 特定于模型的近似方法

1. Linear SHAP（already known）

2. Low-Order SHAP（already known）

3. Max SHAP（novel）

4. Deep SHAP（novel）

Deep SHAP = DeepLIFT + SHAP

---

参考文献：
[1] Ribeiro M T, Singh S, Guestrin C. " Why should i trust you?" Explaining the predictions of any classifier[C]//Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. 2016: 1135-1144.
[2] Štrumbelj E, Kononenko I. Explaining prediction models and individual predictions with feature contributions[J]. Knowledge and information systems, 2014, 41(3): 647-665.
[3] Datta A, Sen S, Zick Y. Algorithmic transparency via quantitative input influence: Theory and experiments with learning systems[C]//2016 IEEE symposium on security and privacy (SP). IEEE, 2016: 598-617.