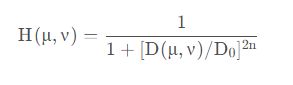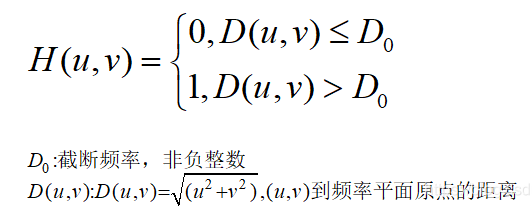图像增强方法概述

目录

一、图像增强的概念

二、图像增强——空域法

2.1 灰度变换

2.1.1 线性变换

2.1.2 分段线性变换

 2.1.3 非线性灰度变换

2.2 直方图修整法

2.2.1 直方图均衡化

2.2.2 直方图规定化

 2.3 图像平滑

2.3.1 邻域平均法（均值滤波）

2.3.2 超限像素平滑法

2.3.3 有选择保边缘平滑法

2.3.4 中值滤波法

2.4 图像锐化

三、图像增强——频域法

3.1 低通滤波

3.2 高通滤波

---

一、图像增强的概念

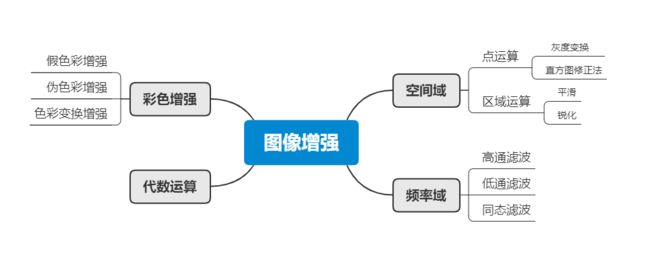
       图像恢复是通过一些先验知识估计图像缺失像素值，是估计值对缺失值的逼近，图像增强则与之不同。图像增强是通过代数或者统计等方法，增强图像中的有用信息，它可以是一个失真的过程，其目的是要改善图像的视觉效果。针对给定图像的应用场合，有目的地强调图像的整体或局部特性，将原来不清晰的图像变得清晰或强调某些感兴趣的特征，扩大图像中不同物体特征之间的差别，抑制不感兴趣的特征，使之改善图像质量、丰富信息量，加强图像判读和识别效果，满足某些特殊分析的需要。根据图像增强所应用的数学方法不同，可以将图像增强方法分为如下图所示的几种方法。

二、图像增强——空域法

本节部分内容来自：https://blog.csdn.net/thecentry/article/details/80720389

       空间域增强是直接对图像各像素进行处理；空间域增强可以分为点运算和局部运算；其中点运算又可以分为：灰度变换、直方图修正法（均衡化、规定化）；局部运算可以分为：图像平滑、图像锐化。

2.1 灰度变换

      灰度变换可调整图像的灰度动态范围或图像对比度，是图像增强的重要手段之一。

2.1.1 线性变换

       令图像 f(i，j) 的灰度范围为[a, b] ，线性变换后图像 g(i ，j) 的范围为[a´，b´ ] ，如图， g(i ，j) 与 f(i ，j) 之间的关系式为：

       在曝光不足或过度的情况下，图像灰度可能会局限在一个很小的范围内。这时在显示器上看到的将是一个模糊不清、似乎没有灰度层次的图像。下图是对曝光不足的图像采用线性变换对图像每一个像素灰度作线性拉伸。可有效地改善图像视觉效果。

2.1.2 分段线性变换

     为了突出感兴趣目标所在的灰度区间，相对抑制那些不感兴趣的灰度区间，可采用分段线性变换。设原图像 f(x,y) 在 [0， M f ], 感兴趣目标的灰度范围在 [a,b], 欲使其灰度范围拉伸到 [c,d], 则对应的分段线性变换表达式为：                          

 2.1.3 非线性灰度变换

          当用某些非线性函数如对数函数、指数函数等，作为映射函数时，可实现图像灰度的非线性变换。

        （1）对数变换

           对数变换的一般表达式为：

          其中 a,b,c 是为了调整曲线的位置和形状而引入的参数。当希望对图像的低灰度区较大的拉伸而对高灰度区压缩时，可采用这种变换，它能使图像灰度分布与人的视觉特性相匹配 

       （2)指数变换

         指数变换的一般表达式为：

          其中参数a,b,c用来调整曲线的位置和形状。这种变换能对图像的高灰度区给予较大的拉伸。

2.2 直方图修整法

        灰度直方图反映了数字图像中每一灰度级与其出现频率间的关系,它能描述该图像的概貌。通过修改直方图的方法增强图像是一种实用而有效的处理技术。

       直方图修整法包括 直方图均衡化及直方图规定化两类。

2.2.1 直方图均衡化

       这种方法通常用来增加图像的全局对比度，尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法，亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度，直方图均衡化通过有效地扩展常用的亮度来实现这种功能。这种方法对于背景和前景都太亮或者太暗的图像非常有用，尤其是可以带来X光图像中更好的骨骼结构显示以及曝光或者曝光不足照片中更好的细节。直方图均衡化的一个主要优势是它是一个相当直观的技术并且是可逆操作，如果已知均衡化函数，那么就可以恢复原始的直方图，并且计算量也不大。当然，这种方法也存在缺点：它对处理的数据不加选择，可能会增加背景的对比度并且降低有用信号的对比度。直方图均衡化是将原图像通过某种变换，得到一幅灰度直方图为均匀分布的新图像的方法。

​
   

​

有关直方图均衡化的数学描述：https://blog.csdn.net/thecentry/article/details/80720389

2.2.2 直方图规定化

       直方图的均衡化自动的确定了变换函数，可以很方便的得到变换后的图像，但是在有些应用中这种自动的增强并不是最好的方法。有时候，需要图像具有某一特定的直方图形状（也就是灰度分布），而不是均匀分布的直方图，这时候可以使用直方图规定化。直方图规定化，也叫做直方图匹配，用于将图像变换为某一特定的灰度分布，也就是其目的的灰度直方图是已知的。这其实和均衡化很类似，均衡化后的灰度直方图也是已知的，是一个均匀分布的直方图；而规定化后的直方图可以随意的指定，也就是在执行规定化操作时，首先要知道变换后的灰度直方图，这样才能确定变换函数。规定化操作能够有目的的增强某个灰度区间，相比于，均衡化操作，规定化多了一个输入，但是其变换后的结果也更灵活。

直方图规定化步骤及代码：图像处理基础(8)：图像的灰度直方图、直方图均衡化、直方图规定化（匹配） - Brook_icv - 博客园

 2.3 图像平滑

        平滑，也可叫滤波，或者合在一起叫平滑滤波，平滑滤波是低频增强的空间域滤波技术。它的目的有两类：一类是模糊；另一类是消除噪音。空间域的平滑滤波一般采用简单平均法进行，就是求邻近像元点的平均亮度值。邻域的大小与平滑的效果直接相关，邻域越大平滑的效果越好，但邻域过大，平滑会使边缘信息损失的越大，从而使输出的图像变得模糊，因此需合理选择邻域的大小。“平滑处理”也称“模糊处理”(blurring)，是一项简单且使用频率很高的图像处理方法。平滑处理的用途很多，但最常见的是用来减少图像上的噪声或者失真。降低图像分辨率时，平滑处理是很重要的。

2.3.1 邻域平均法（均值滤波）

       邻域平均法是典型的线性滤波算法，假设图像由许多灰度恒定的小块组成，相邻的像素之间存在很高的空间相关性，而噪声则是统计独立的。所以可以用邻域内各像素的灰度平均值代替像素原来的灰度值，实现图像的平滑。假设有一副N×N的图像f(x,y)，若平滑图像为g(x,y)，那么我们有：

其中：x, y=0,1,…,N-1，S是(x,y)像素邻域内像素的集合，M表示集合s内像素的个数。这种算法简单，但有一个缺点，就是在降低噪声的同时会使图像产生模糊，特别是在边缘和细节处，而且邻域越大，去噪能力增强的同时模糊程度越严重。

2.3.2 超限像素平滑法

        这种方法对邻域平均法稍加改进。方法把f(x,y)和邻域平均得到的g(x,y)值做一个差的绝对值运算，再与一个选定的阈值进行比较，用比较结果决定像素(x,y)的灰度值g’(x,y)。表达式如下：

        这种方法对抑制椒盐噪声比较有效，对保护仅有微小灰度差的细节和纹理也有效。

2.3.3 有选择保边缘平滑法

       该方法对图像上任一像素(x,y)的5×5邻域，采用9个掩膜，其中包括一个3×3正方形、4个五边形和4个六边形。计算各个掩膜的均值和方差，对方差进行排序，最小方差所对应的掩膜区的灰度均值就是像素(x,y)的输出值。

        这种方法用方差来测度区域的灰度均匀性。如果区域含有尖锐的边缘，它的灰度方差就会很大，如果不含边缘或者灰度均匀的区域，方差就很小，所以最小方差所对应的区域就是灰度最均匀区域。这种平滑方法既能消除噪声，又不会破坏区域边界的细节。另外，五边形和六边形在(x,y)处都有锐角，这样，即使像素(x,y)位于一个复杂形状区域的锐角处，也能找到均匀的区域。从而在平滑时既不会使尖锐边缘模糊，也不会破坏边缘形状。

2.3.4 中值滤波法

       中值滤波法用一个滑动窗口，对窗口内的像素灰度排序，用中值代替窗口中心像素的灰度值，是一种非线性的图像平滑法。

        中值滤波器的窗口形状可以有多种，如线状、方形、十字形、圆形、菱形等。不同形状的窗口会产生不同的滤波效果，在使用的时候需要根据图像的内容和不同的要求进行选择。经验表明方形或圆形的窗口适宜于外轮廓线较长的物体图像，而十字形窗口对有尖顶角状的图像效果好。

本节内容来自（案例处有案例及代码）：https://blog.csdn.net/weixin_44221738/article/details/108951263

2.4 图像锐化

       图像锐化(image sharpening)是补偿图像的轮廓，增强图像的边缘及灰度跳变的部分，使图像变得清晰，分为空间域处理和频域处理两类。图像锐化是为了突出图像上地物的边缘、轮廓，或某些线性目标要素的特征。这种滤波方法提高了地物边缘与周围像元之间的反差，因此也被称为边缘增强。图像锐化的方法可以大致分为两类：微分法、高频加重滤波法。其中微分法可以分为梯度法、Sobel算子法、Laplace算子法等。

有关图像锐化的数学原理请参考：

https://blog.csdn.net/baishuiniyaonulia/article/details/98480583

有关图像锐化的matlab实现及测试数据：

https://blog.csdn.net/weixin_42429718/article/details/106902377

锐化算子的python实现：【图像处理】轻松搞懂图像锐化 - 知乎

三、图像增强——频域法

        图像增强技术基本上可分成两大类：频域处理法和空域处理法。频域处理法[1]的基础是卷积定理，它采用修改图像傅立叶变换的方法实现对图像的增强处理。在频域空间，图像的信息表现为不同频率分量的组合。如果能让某个范围内的分量或某些频率的分量受到抑制而让其他分量不受影响，就可以改变输出图的频率分布，达到不同的增强目的。频域增强是利用图像变换方法将原来的图像空间中的图像以某种形式转换到其它空间中，然后利用该空间的特有性质方便地进行图像处理，最后再转换回原来的图像空间中，从而得到处理后的图像。

频域增强的主要步骤是：

(1) 选择变换方法，将输入图像变换到频域空间；

(2) 在频域空间中，根据处理目的设计一个转移函数并进行处理；

(3) 将所得结果用反变换得到图像增强。

卷积理论是频域技术的基础。设函数f（x,y）与线性位不变算子h（x,y）的卷积结果是g（x,y），即g(x,y)=h(x,y)*f(x,y)

那么根据卷积定理在频域有：

               

其中G(x,y)、 H(u,v)、F(u,v)分别是g(x,y)、h(x,y)、f(x,y)的傅立叶变换。

（4）技术所需增强图的傅立叶变换。

（5）将其与一个（根据需要设计的）转移函数相乘。

（6）再将结果进行傅立叶反变换以得到增强的图。

（7）将图像从空域转换到频域所需的变换及将图像从频域空间转换回空域所需的变换。

（8）在频域空间对图像进行增强加工操作。

常用的频域增强方法有低通滤波和高通滤波。

频域法概述引自博客：
https://blog.csdn.net/ccsss22/article/details/109349584

3.1 低通滤波

        图像的平滑除了在空间域中进行外，也可以在频域中进行。对于一幅图像，它的边缘、细节、跳跃部分以及噪声都代表图像的高频分量，而大面积的背景区域和缓慢变化部分则代表图像的低频分量。为了去除噪声改善图像质量，滤波器采用低通滤波器H(u,v)来抑制高频成分，通过低频成分，然后再进行逆傅里叶变换获得滤波图像，就可达到平滑图像的目的。不同类型的低通滤波器实现的效果有所差异。理想低通滤波器会产生比较严重的振铃现象，为了改善振铃效应，可以采用巴特沃斯低通滤波器和指数低通滤波器（略）。

巴特沃斯低通滤波器的冲激函数定义为：

巴特沃斯低通滤波器的空域图像：
可以与上图理想圆形低通滤波器的空域图像对比，振铃效应减弱很多

3.2 高通滤波

       高通滤波是要保留图象中的高频分量而除去低频分量。因为图像中的边缘对应高频分量，所以锐化图像可以使用高通滤波。理想高通滤波：

 高通滤波的理论原理：高通滤波的图像增强之频域滤波 - acwarming - 博客园

高通滤波的python代码实现：3.3 Python图像的频域图像增强-特殊高通滤波器_集电极的博客-CSDN博客_python频域法数据增强