机器学习 | 关于决策树分类模型,你学得怎么样了?
这是一篇关于决策树分类模型的详解,身边的朋友看完的都说:这回透彻了!
目录
0 写在前面
1 决策树分类模型
1.1 信息熵
1.2 基尼系数
2 决策树分类模型的建立
3 总结一下
0 写在前面
机器学习分为有监督学习和无监督学习,有监督学习又可以分为分类和回归两大类。本文介绍的决策树分类模型属于有监督学习中的分类算法,也就是说:我们的训练数据有一组与之对应的目标数据,这组目标数据是一组不连续的、存在重复的值。我们就是用这样的数据训练出需要的决策树分类模型。是的,你没有听错,模型由我们的训练数据决定。
实际应用中,我们会将数据分为两部分,一部分称为训练集,另一部分称为测试集。训练集用于训练模型,测试集用于评估模型。此外,为增加结果的说服力,我们还会进行K折交叉验证,对于涉及参数设置的模型,我们还会进行参数调优。这些都将借助scikit-learn机器学习包实现,需要提前在Python环境中安装。专栏中关于模型评估、交叉验证和参数调优的内容将在后期的文章中做专门的阐述,以求把一个个模型讲清楚,同时避免因内容繁杂而增加学习负担。
你不会被专业名词吓到吧?跟着文章的思路,你会发现它们其实很简单。
1 决策树分类模型
在众多机器学习算法模型中,决策树分类模型属于比较好理解的一种。它的基本原理是一系列的逻辑判断,很接近人类的决策思路,也很接近编程中的 if/else逻辑。
建立决策树模型,关键在于确定每个节点应该选择哪个特征变量。也就是明确建立决策树的依据。为了加深理解,我们先观察下面两个决策树:
你认为哪一个决策树更好,更合理?你会选择决策树1吗?
很显然,我们要的是有区分度的特征。区分度最高的特征可以作为根节点,越远离根节点的特征,其区分度也就越低。符合这一规律的决策树才是一个合理的决策树。 问题是,怎样量化特征的区分度呢?我们不妨换个角度想:一个混乱的系统经过某一特征的分类后,系统的各部分出现了一定的秩序,使得系统整体的混乱程度得以降低,是不是就能说明这个特征具有区分度?而最能降低系统混乱程度的特征具有最高的区分度,将被选为根节点?答案是肯定的,决策树模型也是这么做的。
此时,问题变成了如何量化混乱程度?而这正是信息熵和基尼系数的作用。
1.1 信息熵
香农(C.E.Shannon)借鉴热力学概念,于1948年提出了信息熵。信息熵是衡量系统混乱程度的经典指标。信息熵的最大值为1,最小值为0。信息熵越大说明系统的混乱程度越大。信息熵的计算公式如下:
![]()
![]() 是X系统中
是X系统中![]() 出现的频率,当依据某一特征,将系统X分为 i 个部分后,所有部分的信息熵之和称为条件熵
出现的频率,当依据某一特征,将系统X分为 i 个部分后,所有部分的信息熵之和称为条件熵![]() 。
。![]() 是部分样本占系统样本总数的比值。条件熵计算公式如下:
是部分样本占系统样本总数的比值。条件熵计算公式如下:
![]()
抽象,太抽象了!这里用实例具体说明一下:
说明猫和狗的叫声特征具有完全的区分度,消除了混乱。
1.2 基尼系数
基尼系数同样是衡量系统失序程度的指标,但相较于信息熵,基尼系数的计算更加简单,决策树模型也更多地使用基尼系数。基尼系数最大值0.5,最小值0。同样是数值越大,系统越混乱。计算公式如下:
![]()
![]() 是X系统中
是X系统中![]() 出现的频率,当依据某一特征,将系统X分为 i 个部分后,基尼系数的计算公式如下:
出现的频率,当依据某一特征,将系统X分为 i 个部分后,基尼系数的计算公式如下:
![]()
抽象,太抽象了!用同一个实例具体说明一下:
说明猫和狗的叫声特征具有完全的区分度,消除了混乱。所得结论与信息熵的结论是一样的。
2 决策树分类模型的建立
分类决策树的理论部分已经在上一小节做了详细陈述,该小节是关于如何用Pyhton实现分类决策树模型。过程中我们会用到scikit-learn库和 iris.csv数据集。
import pandas as pd
data=pd.read_csv('iris.csv')
print(data.sample(5))
# 数据展示如下:
'''
sepal_length sepal_width petal_length petal_width species
37 4.9 3.6 1.4 0.1 setosa
128 6.4 2.8 5.6 2.1 virginica
144 6.7 3.3 5.7 2.5 virginica
90 5.5 2.6 4.4 1.2 versicolor
111 6.4 2.7 5.3 1.9 virginica
'''
data.species=df.species.map({'setosa':0,'virginica':1,'versicolor':2})
print(data.sample(5)) # df.sample()随机取样,故前后两次所取数据不一样
'''
sepal_length sepal_width petal_length petal_width species
43 5.0 3.5 1.6 0.6 0
46 5.1 3.8 1.6 0.2 0
74 6.4 2.9 4.3 1.3 2
14 5.8 4.0 1.2 0.2 0
75 6.6 3.0 4.4 1.4 2
'''iris.csv中保存了安德森鸢尾花卉数据集,数据集的容量为150行×5列。其中前四列是花萼和花瓣的长宽,第五列是花卉的品种。在开始训练模型前,还有一步必须完成,将species列的数据做数值化处理。这是因为Python数学建模中无法识别文本数据。
X=data.drop(columns='species')
y=data.species
# sklearn中有专门划分训练集和测试集的函数,test_size表示测试集占整个数据集的比例
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=1)
from sklearn.tree import DecisionTreeClassifier
model=DecisionTreeClassifier(max_depth=3,random_state=123)
# max_depth设置决策树最大深度(简单理解就是判断次数)
model.fit(X_train,y_train)
y_pre=model.predict(X_test) # 模型根据测试集特征变量预测花卉品种species
score=model.score(X_test,y_test) # 预测结果与真实品种对比,返回正确率
print('accuracy score:','{:.2%}'.format(score))
# 返回打分结果score,结果为0.9667,说明模型对测试集的预测准确率为96.67%
'''
accuracy score: 96.67%
'''
在训练模型的时候,我们只导入过程中需要用到的部分,因为scikit-learn比较大,整个导入需占用较大内存。
imp=model.feature_importances_
features_imp=pd.Series(imp,index=X.columns,name='features_imp')
print(features_imp)
# 返回各特征变量的重要性:
'''
sepal_length 0.000000
sepal_width 0.000000
petal_length 0.595136
petal_width 0.404864
Name: features_imp, dtype: float64
'''feature_importances_返回一个浮点数列表,所有元素之和等于1。列表的元素个数等于特征变量个数,表示各特征变量在决策树中的重要性,反映了各特征变量的区分度高低。那么,这些数值是怎样得出的呢?下面将详细说明这个问题。为了让过程更加直观,我们运行下面的代码,把我们建立的决策树作图画出:
import graphviz
from sklearn.tree import export_graphviz
import os
os.environ['PATH']=os.pathsep+r'C:\Program Files (x86)\Graphviz2.38\bin'
dot_data=export_graphviz(model,out_file=None,
feature_names=X.columns,
class_names=['setosa','virginica','versicolor'],
filled=True, rounded=True,
special_characters=True)
graph=graphviz.Source(dot_data)
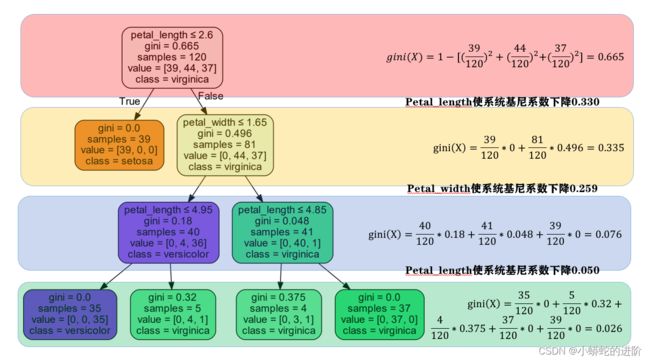
graph.render('result') # 此处可以是绝对路径,如:E:\\python_outputs\\result我们用到了Graphviz,这是一个开源的做图软件,在使用它之前,我们不仅要安装软件,还要安装相应的python模块graphviz。下图就是我们建立的决策树:
越往下,系统整体的基尼系数越小,基尼系数下降的幅度也越小。整个决策树让系统的基尼系数下降了0.639,其中Petal_length贡献了(0.330+0.050),Petal_width贡献了0.259。通过计算:
- petal_length:(0.330+0.050)/ 0.639 = 0.595
- petal_width: 0.259 / 0.639 = 0.405
与feature_importances_导出的结果一致(只有小数位数不一样)。同时,仔细发现:当基尼系数为0时,决策树不再分支,当基尼系数不为0时则取决于是否达到max_depth参数设定的最大深度,达到最大深度后也是不再分支的。最后看一下模型的预测花卉品种的概率:
y_predict_proba=model.predict_proba(X_test)
# 将y_predict_proba结果放进DataFrame,注意columns依次对应0,1,2代表的花卉名。
proba_df=pd.DataFrame(y_predict_proba,columns=['setosa','virginica','versicolor'])
print(proba_df.head())
'''
setosa virginica versicolor
0 1.0 0.0 0.0
1 0.0 0.0 1.0
2 0.0 0.0 1.0
3 1.0 0.0 0.0
4 0.0 1.0 0.0
'''概率都是1,100%确定。暂不讨论是否合理,我们看看是怎么来的。先看X_test数据:
print(X_test.head())
'''
sepal_length sepal_width petal_length petal_width
14 5.8 4.0 1.2 0.2
98 5.1 2.5 3.0 1.1
75 6.6 3.0 4.4 1.4
16 5.4 3.9 1.3 0.4
131 7.9 3.8 6.4 2.0
'''模型对第一各X_test样本的预测结果是:100%为品种setosa。达到这一结果,我们只需要不样本的特征数据放到决策树中,从上到下直至最终的分节点。如输出的14号样本,petal_length=1.2,小于2.6,被分类为class:setosa。概率=39 /(39+0+0)= 1。其他样本依次类推。
在学习分类决策树模型时,如果你能理解上图决策树以及所涉及的计算,说明你已经很好地掌握了该模型。
所以,你学会了吗?
3 总结一下
文章中对决策树模型做了理论和实践上的介绍,如果相对模型算法有更深入的认识,可以重点阅读文章中信息熵、基尼系数和Graphviz决策树图部分。下一篇我们将介绍逻辑回归分类模型。
是的,没有打错字!逻辑回归是用于分类的,只是有一颗回归的心。
点赞+关注,你的鼓励,我的动力。爱你!