Python+OpenCV 实现简单的高斯滤波
基本原理讲解:高斯模糊的算法 - 阮一峰的网络日志
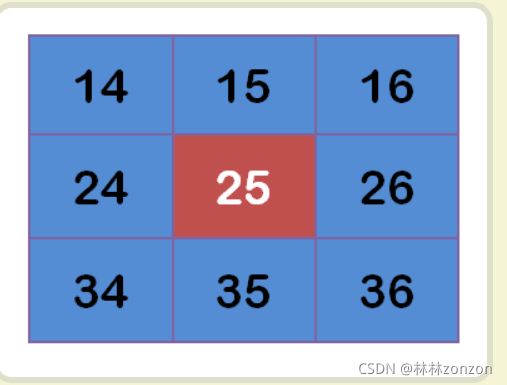
高斯核函数的编写:构建权重矩阵,采用高斯二维分布函数的形式进行处理。需要注意的是,这里我没有特判当sigma = 0的时候的情况。
即是实现:
1)权重矩阵的构建
计算矩阵内部结构,其中因为要进行归一化处理,e前方的系数会被约去,因此代码中不体现。
2)矩阵元素归一化处理
计算矩阵内部元素总和sum,最后做矩阵除法得到归一化处理后的权重矩阵。
# 高斯核生成函数 kernel_size:滤波核大小 sigma:高斯核函数的局部影响范围
def gauss(kernel_size, sigma):
#定型0填充
kernel = np.zeros((kernel_size, kernel_size))
#确定正态分布中间值
center = kernel_size // 2
# s:方差 sum:记录总和
s = sigma ** 2
sum = 0
for i in range(kernel_size):
for j in range(kernel_size):
#由于最后要进行归一化处理,此处根号下2Π计算可以省略
x, y = i - center, j - center
kernel[i, j] = np.exp(-(x ** 2 + y ** 2) / (2 * s))
sum += kernel[i, j]
#归一化处理后输出
kernel = kernel / sum
return kernel滤波函数的编写:将图片中的每个像素点(边缘除外)及其周围像素乘以权重矩阵,实现高斯滤波
需要注意的是此函数仅能处理彩色图片,因为只有彩色图片拥有img.shape[2]元素,灰度图片没有img.shape[2]元素不能用这个方法处理。
# 高斯滤波实现,img:输入图像 kermel:输入高斯核函数
def myfilter(img,kernel):
# 读取img行数核列数
h = img.shape[0]
w = img.shape[1]
# 直接拷贝父对象
img1 = copy.copy(img)
# 去掉边缘
for i in range(1,h-1):
for j in range(1,w-1):
# 三通道处理
for c in range(0,2):
sum = 0
# 加权
for k in range(-1,2):
for l in range(-1,2):
sum += img[i+k,j+l,c]*kernel[k+1,l+1]
img1[i,j,c] = sum
return img1同时在处理高斯滤波的时候,函数采取的是针对3*3的kernel_size进行编写的,要更改kernel_size的大小,需要更改此处的range范围。 
下面是灰度图像的处理方式:
def myfilter2(img,kernel):
# 读取img行数核列数
h = img.shape[0]
w = img.shape[1]
# 直接拷贝父对象
img1 = copy.copy(img)
# 去掉边缘
for i in range(1,h-1):
for j in range(1,w-1):
sum = 0
for k in range(-1,2):
for l in range(-1,2):
sum += img[i+k,j+l]*kernel[k+1,l+1]
img1[i,j] = sum
return img1最后整个运行代码:
import copy
import cv2
import numpy as np
#图像读取
img_y = cv2.imread('p2.jpg')
# 选择高斯生成函数3*3,其中sigama = 3
kernel = gauss(3,3)
# 打印这个生成函数
print(kernel)
# 高斯滤波处理
img1 = myfilter(img_y, kernel)
cv2.imshow('P1_yuantu',img_y)
cv2.imshow('P1_gaussian', img1)
cv2.waitKey(0)输入输出图像结果展示:
原图与高斯滤波后
需要注意的是采取的方法很原始,如果输入的图像过大,运行时间会很久。
这方面东西挺有意思的,只是初略的学习,写些基础的东西,应该还有错漏的地方,希望有大佬们多多指点。