西瓜书第六章课后题

本文章有的是自己做的，有的是参考其他人的答案，毕竟能力有限，完全使用的放上原博主的博客，仅做自己个人学习使用。如有冒犯和侵权，本人会立刻进行删除，感谢这些能做出来的大神。

6.1

试证明样本空间中任一点$x$到超平面$(w,b)$的距离为式6.2
$$r=\frac{|w^{T}x+b|}{||w||}(6.2)$$

答：
①设超平面为$w^T+b=0$,其法向量为$w$，设空间中一点为$x_1$，且平面上存在一点$x_2$，使得$(x_2-x_1)$与超平面垂直。
这一步其实就是做了一个垂直于这个超平面的法向量。
②则有$$(x_2-x_1)=\eta w(其中\eta \in R);(1)$$
③$点x_1到超平面的距离为：$
$$r=|(x_2-x_1{)}^T(x_2-x_1){|}^{\frac{1}{2}}=|\eta |\ast ||w|{|}_2;(2)$$
根据点$x_2$在超平面上，所以$$w^T{x}_2+b=0(3)$$,将（1）带入（3）消去$x_2$得：
$$w^T{x}_1+b=-\eta ||w|{|}_2^2$$,两边取绝对值得，$$|w^T{x}_1+b|=|\eta |\ast ||w|{|}_2^2(4)$$
即$$|\eta |=\frac{|w^T{x}_1+b|}{||w|{|}_2^2}$$
④将（4）带入（2）得：$$r=\frac{|w^{T}x+b|}{||w||}$$证毕

6.2

试使用LIBSVM在西瓜数据集3.0$\alpha$上分别使用线性核和高斯核训练一个SVM，并比较其支持向量的差别。
原文链接西瓜书第六章课后习题从一开始就讲的特别详细，太猛了。
代码如下：

from sklearn import svm
from sklearn.model_selection import cross_val_score

X=[
    [1.   , 2.   , 1.   , 0.   , 2.   , 1.   , 0.697, 0.46 ],
    [2.   , 2.   , 0.   , 0.   , 2.   , 1.   , 0.774, 0.376],
    [2.   , 2.   , 1.   , 0.   , 2.   , 1.   , 0.634, 0.264],
    [1.   , 2.   , 0.   , 0.   , 2.   , 1.   , 0.608, 0.318],
    [0.   , 2.   , 1.   , 0.   , 2.   , 1.   , 0.556, 0.215],
    [1.   , 1.   , 1.   , 0.   , 1.   , 0.   , 0.403, 0.237],
    [2.   , 1.   , 1.   , 1.   , 1.   , 0.   , 0.481, 0.149],
    [2.   , 1.   , 1.   , 0.   , 1.   , 1.   , 0.437, 0.211],
    [2.   , 1.   , 0.   , 1.   , 1.   , 1.   , 0.666, 0.091],
    [1.   , 0.   , 2.   , 0.   , 0.   , 0.   , 0.243, 0.267],
    [0.   , 0.   , 2.   , 2.   , 0.   , 1.   , 0.245, 0.057],
    [0.   , 2.   , 1.   , 2.   , 0.   , 0.   , 0.343, 0.099],
    [1.   , 1.   , 1.   , 1.   , 2.   , 1.   , 0.639, 0.161],
    [0.   , 1.   , 0.   , 1.   , 2.   , 1.   , 0.657, 0.198],
    [2.   , 1.   , 1.   , 0.   , 1.   , 0.   , 0.36 , 0.37 ],
    [0.   , 2.   , 1.   , 2.   , 0.   , 1.   , 0.593, 0.042],
    [1.   , 2.   , 0.   , 1.   , 1.   , 1.   , 0.719, 0.103]
]
y=[1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0]

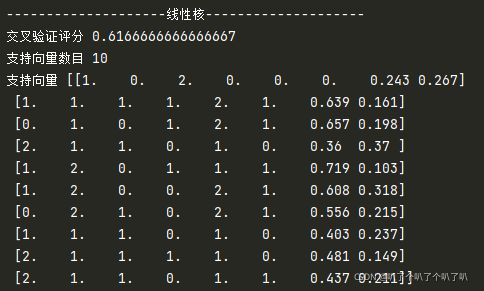
print("-"*20+"线性核"+"-"*20)
clf1=svm.SVC(C=1,kernel='linear')
print("交叉验证评分",cross_val_score(clf1,X,y,cv=5,scoring='accuracy').mean())
clf1.fit(X,y)
print("支持向量数目",clf1.n_support_.sum())
print("支持向量",clf1.support_vectors_)

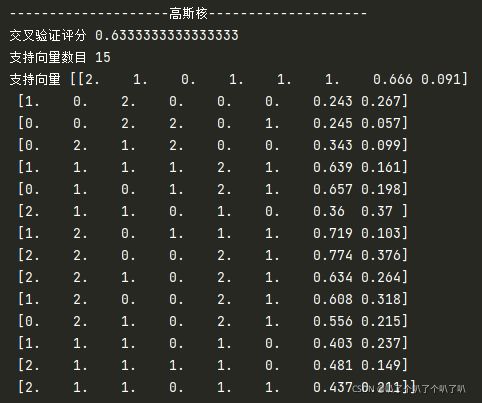
print("-"*20+"高斯核"+"-"*20)
clf2=svm.SVC(C=1,kernel='rbf')
print("交叉验证评分",cross_val_score(clf2,X,y,cv=5,scoring='accuracy').mean())
clf2.fit(X,y)
print("支持向量数目",clf2.n_support_.sum())
print("支持向量",clf2.support_vectors_)

用完人家的自己也得搞懂

clf1=svm.SVC(C=1,kernel='linear')//是在我的理解里是建立了一个svm分类器对象，kernel是这个分类器是用什么样的核函数，这里的是线性核
clf1.fit(x,y)//用训练数据拟合分类器模型
//后面几个就是print里的作用

最后得到两种不一样的分析结果，在C相同的情况下，可以看出高斯核的评分是要高于线性核的，在模型复杂度上，高斯核的支持向量数目也比较多，所以应该是高斯核比较复杂。这里本来想进行数据可视化，结果发现原来显示出来的图只是跟着书上敲出来的，一自己做就傻眼了，决定在这里回过头去再把数据可视化学习一下。

6.3

还没看决策树和神经网络，是看着胡浩基老师的课来学的这本书，等着学完了再回来做这道题。