机器学习笔记之高斯网络(三)高斯马尔可夫随机场

引言

上一节介绍了高斯贝叶斯网络(Gaussian Bayesian Network,GBN)，本节将介绍基于高斯网络的无向图模型——高斯马尔可夫随机场。

回顾：马尔可夫随机场——团、势函数

不同于贝叶斯网络，马尔可夫随机场中结点之间的边没有方向性，这使得没有办法直接通过概率图结构描述因子分解式。
因而通过团(Clique)、势函数(Potential Functions)对无向图结点的联合概率分布 进行描述：

已知一个马尔可夫随机场泛型 表示如下：
为什么说是泛型呢~在描述马尔可夫随机场的结构时，为了突出某个具体结构，没有将所有结点之间的关联关系进行描述，从而仅通过一个结点对某一部分子图进行整体概括。相关视频传送门——信念传播

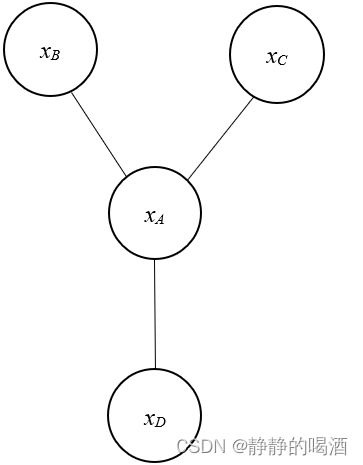
其中${\mathcal{X}}_{\mathcal{A}},{\mathcal{X}}_{\mathcal{B}},{\mathcal{X}}_{\mathcal{C}},{\mathcal{X}}_{\mathcal{D}}$分别表示四个子图。该图中更需要突出的是这四个子图之间的关联关系。
观察，图中一共包含$3$个最大团：$\{{\mathcal{X}}_{\mathcal{A}},{\mathcal{X}}_{\mathcal{B}}\},\{{\mathcal{X}}_{\mathcal{A}},{\mathcal{X}}_{\mathcal{C}}\},\{{\mathcal{X}}_{\mathcal{A}},{\mathcal{X}}_{\mathcal{D}}\}$

对应该图结点的联合概率分布$\mathcal{P}(\mathcal{X})$表示如下：
$$\mathcal{P}(\mathcal{X})=\frac{1}{\mathcal{Z}}[{\psi }_{\mathcal{A}\mathcal{B}}({\mathcal{X}}_{\mathcal{A}},{\mathcal{X}}_{\mathcal{B}})\cdot {\psi }_{\mathcal{A}\mathcal{C}}({\mathcal{X}}_{\mathcal{A}},{\mathcal{X}}_{\mathcal{C}})\cdot {\psi }_{\mathcal{A}\mathcal{D}}({\mathcal{X}}_{\mathcal{A}},{\mathcal{X}}_{\mathcal{D}})\cdot {\psi }_{\mathcal{A}}({\mathcal{X}}_{\mathcal{A}})\cdot {\psi }_{\mathcal{B}}({\mathcal{X}}_{\mathcal{B}})\cdot {\psi }_{\mathcal{C}}({\mathcal{X}}_{\mathcal{C}})\cdot {\psi }_{\mathcal{D}}({\mathcal{X}}_{\mathcal{D}})]$$

因而基于随机变量集合$\mathcal{X}=(x_1,x_2,\cdots ,x_p{)}^T，$可以将无向图的联合概率分布$\mathcal{P}(\mathcal{X})$表示为如下形式：
这里假设每个结点中仅包含一个随机变量。
$$\mathcal{P}(\mathcal{X})=\frac{1}{\mathcal{Z}}\prod _{i=1}^p{\psi }_i(x_i)\cdot \prod _{x_i,x_j\in \mathcal{X}}{\psi }_{ij}(x_i,x_j)$$
称${\psi }_i(x_i)$为点势函数(Node Potential)，称${\psi }_{ij}(x_i,x_j)$为边势函数(Edge Potential)。

高斯马尔可夫随机场

即便是无向图模型，随机变量集合$\mathcal{X}$的联合概率分布$\mathcal{P}(\mathcal{X})$依然服从多元高斯分布：
$$\mathcal{P}(\mathcal{X})=\frac{1}{(2\pi {)}^{\frac{p}{2}}|\Sigma {|}^{\frac{1}{2}}}\exp \left[-\frac{1}{2}(\mathcal{X}-\mu {)}^T{\Sigma }^{-1}(\mathcal{X}-\mu )\right]$$
目标是将多元高斯分布和势函数联系在一起：

• 观察多元高斯分布$\mathcal{P}(\mathcal{X})$，其中$\frac{1}{(2\pi {)}^{\frac{p}{2}}|\Sigma {|}^{\frac{1}{2}}}$中的$\Sigma$是模型自身参数，和$\mathcal{X}$无关。因此对$\mathcal{P}(\mathcal{X})$进行如下表示：
  对${\Sigma }^{-1}$使用‘精度矩阵’$\Lambda$进行表示。
  $$\begin{array}{rl}\mathcal{P}(\mathcal{X})& \propto \exp \left[-\frac{1}{2}(\mathcal{X}-\mu {)}^T{\Sigma }^{-1}(\mathcal{X}-\mu )\right]\\ & =\exp \left[-\frac{1}{2}(\mathcal{X}-\mu {)}^T\Lambda (\mathcal{X}-\mu )\right]\end{array}$$
• 将中括号内部元素展开，有：
  $\Delta$表示原式。
  $$\begin{array}{rl}\Delta & =\exp \left[-\frac{1}{2}({\mathcal{X}}^T\Lambda -{\mu }^T\Lambda )(\mathcal{X}-\mu )\right]\\ & =\exp \left[-\frac{1}{2}\left({\mathcal{X}}^T\Lambda \mathcal{X}-{\mathcal{X}}^T\Lambda \mu -{\mu }^T\Lambda \mathcal{X}+{\mu }^T\Lambda \mu \right)\right]\end{array}$$
  此时观察小括号中的${\mathcal{X}}^T\Lambda \mu$和${\mu }^T\Lambda \mathcal{X}$，其中$\mathcal{X},\mu$都是$p\times 1$的列向量，$\Lambda$ 是一个$p\times p$的矩阵。因而有：
  它们结果均是实数，根据‘乘法交换律’，结果是相等的~
  $$\begin{array}{rl}{\mathcal{X}}^T\Lambda \mu ={\mu }^T\Lambda \mathcal{X}& =(x_1,\cdots ,x_p)\left(\begin{array}{c}{\lambda }_{11},{\lambda }_{12},\cdots ,{\lambda }_{1p}\\ {\lambda }_{21},{\lambda }_{22},\cdots ,{\lambda }_{2p}\\ ⋮\\ {\lambda }_{p1},{\lambda }_{p2},\cdots ,{\lambda }_{pp}\end{array}\right)\left(\begin{array}{c}{\mu }_1\\ {\mu }_2\\ ⋮\\ {\mu }_p\end{array}\right)\\ & =\left[\sum _{i=1}^p{x}_i{\lambda }_{i1},\cdots ,\sum _{i=1}^p{x}_i{\lambda }_{ip}\right]\left(\begin{array}{c}{\mu }_1\\ {\mu }_2\\ ⋮\\ {\mu }_p\end{array}\right)\\ & =\sum _{j=1}^p\sum _{i=1}^p{x}_i\cdot {\lambda }_{ij}\cdot {\mu }_j\end{array}$$
  将这两项合并，有：
  $$\Delta =\exp \left[-\frac{1}{2}\left({\mathcal{X}}^T\Lambda \mathcal{X}-2{\mu }^T\Lambda \mathcal{X}+{\mu }^T\Lambda \mu \right)\right]$$
• 继续观察，其中${\mu }^T\Lambda \mu$依然是模型参数表示的量，和$\mathcal{X}$无关。因此原式可表示为：
  精度矩阵$\Lambda$本身是‘实对称矩阵’，因而有${\Lambda }^T=\Lambda$,从而有${\mu }^T{\Lambda }^T=(\Lambda \mu {)}^T.$
  $$\begin{array}{rl}\Delta & \propto \exp \left[-\frac{1}{2}{\mathcal{X}}^T\Lambda \mathcal{X}+{\mu }^T\Lambda \mathcal{X}\right]\\ & =\exp \left[-\frac{1}{2}{\mathcal{X}}^T\Lambda \mathcal{X}+{\left(\Lambda \mu \right)}^T\mathcal{X}\right]\end{array}$$
  观察中括号中的项，其中$-\frac{1}{2}{\mathcal{X}}^T\Lambda \mathcal{X}$是关于$\mathcal{X}$的二次项；${\left(\mu \Lambda \right)}^T\mathcal{X}$是关于$\mathcal{X}$的一次项。

称$\Lambda \mu$为势向量(Potential Vector)。

点势函数关联的项

关于某一维特征$x_i$，观察哪些项只和$x_i$相关？

• 首先观察$-\frac{1}{2}{\mathcal{X}}^T\Lambda \mathcal{X}$，将它展开：
  $$\begin{array}{rl}-\frac{1}{2}{\mathcal{X}}^T\Lambda \mathcal{X}& =-\frac{1}{2}\left[(x_1,\cdots ,x_p)\left(\begin{array}{c}{\lambda }_{11},{\lambda }_{12},\cdots ,{\lambda }_{1p}\\ {\lambda }_{21},{\lambda }_{22},\cdots ,{\lambda }_{2p}\\ ⋮\\ {\lambda }_{p1},{\lambda }_{p2},\cdots ,{\lambda }_{pp}\end{array}\right)\left(\begin{array}{c}{x}_1\\ ⋮\\ x_p\end{array}\right)\right]\\ & =-\frac{1}{2}\left[\sum _{i=1}^p{x}_i{\lambda }_{i1},\cdots ,\sum _{i=1}^p{x}_i{\lambda }_{ip}\right]\left(\begin{array}{c}{x}_1\\ ⋮\\ x_p\end{array}\right)\\ & =-\frac{1}{2}\sum _{j=1}^p\sum _{i=1}^p{x}_i\cdot x_j\cdot {\lambda }_{ij}\end{array}$$
  该展开式中仅和$x_i$相关的项只有：
  $$-\frac{1}{2}{x}_i\cdot x_i\cdot {\lambda }_{ii}$$
• 然后观察${\left(\mu \Lambda \right)}^T\mathcal{X}$，展开结果如下：
  $$\begin{array}{rl}{\left(\mu \Lambda \right)}^T\mathcal{X}& ={\left[\left(\begin{array}{c}{\lambda }_{11},{\lambda }_{12},\cdots ,{\lambda }_{1p}\\ {\lambda }_{21},{\lambda }_{22},\cdots ,{\lambda }_{2p}\\ ⋮\\ {\lambda }_{p1},{\lambda }_{p2},\cdots ,{\lambda }_{pp}\end{array}\right)\left(\begin{array}{c}{\mu }_1\\ ⋮\\ {\mu }_p\end{array}\right)\right]}^T\left(\begin{array}{c}{x}_1\\ ⋮\\ x_p\end{array}\right)\\ & =\left[\sum _{i=1}^p{\lambda }_{1i}\cdot {\mu }_i,\cdots ,\sum _{i=1}^p{\lambda }_{pi}\cdot {\mu }_i\right]\left(\begin{array}{c}{x}_1\\ ⋮\\ x_p\end{array}\right)\\ & =\sum _{j=1}^p\sum _{i=1}^p{\lambda }_{ji}\cdot {\mu }_i\cdot x_j\end{array}$$
  其中和$x_i$有关的项一共有$p$项：
  $$\underset{p项}{{\lambda }_{i1}\cdot {\mu }_1\cdot x_i,\cdots ,{\lambda }_{ip}\cdot {\mu }_p\cdot x_i}$$
  如果令$\mathcal{H}=(h_1,\cdots ,h_p)=\Lambda \mu$，对应的$h_i$项就是只与$x_i$有关的项：
  $$h_i=\sum _{k=1}^p{\lambda }_{ik}\cdot {\mu }_k$$

至此，仅和$x_i$相关的项表示如下：
$$-\frac{1}{2}{x}_i\cdot x_i\cdot {\lambda }_{ii}+h_i\cdot x_i$$

边势函数相关的项

同理，观察哪些项与$x_i,x_j$同时相关？
这里就不重新展开了，感兴趣的小伙伴可以自行找一下~

• 二次项中和$x_i,x_j$同时相关的项：
  因为精度矩阵$\Lambda$是实对称矩阵，因而有${\lambda }_{ij}={\lambda }_{ji}$.
  $$-\frac{1}{2}[x_i\cdot x_j\cdot {\lambda }_{ij}+x_j\cdot x_i\cdot {\lambda }_{ji}]=-{\lambda }_{ij}\cdot x_i\cdot x_j$$
• 一次项不可能同时与$x_i,x_j$相关，因此自然是没有的~

至此，可以将仅关于单个点$x_i(i=1,2,\cdots ,p)$的项看作点势函数的表示；将关于两个结点$x_i,x_j(i,j\in \{1,2,\cdots ,p\};i\ne j)$的项看作边势函数的表示。

关于多元高斯分布学习任务的核心思想

通过上述描述可以发现，如果${\lambda }_{ij}=0$，意味着结点$x_i,x_j$之间的边势函数为零，因而$x_i,x_j$两结点之间不存在边直接相连：
该推导过程本质上就是‘精度矩阵与条件独立性’的证明。如果两结点之间不存在直接相连的边，根据成对马尔可夫性,这两个结点就是相互独立的。
$$x_i\perp x_j\mid x_{-i-j}\iff {\lambda }_{ij}=0$$

从高斯网络的角度去观察 多元高斯分布模型参数$\mu ,\Sigma$的学习任务(Learning)，发现它不仅仅学习了参数，还学习了各维度特征之间的结构关系(精度矩阵$\Lambda =[{\lambda }_{ij}{]}_{p\times p}$)。

关于条件独立性的总结

从特征之间独立性的角度观察：

• 边缘相互独立/绝对相互独立(Marginal Independent)：
  $$x_i\perp x_j;\Sigma =[{\sigma }_{ij}{]}_{p\times p}\iff {\sigma }_{ij}=0$$

• 条件独立性(Conditional Independence)：
  $$x_i\perp x_j\mid x_{-i-j};\Lambda ={\Sigma }^{-1}=[{\lambda }_{ij}{]}_{p\times p}\iff {\lambda }_{ij}=0$$

• 对于任意一个高斯马尔可夫随机场，关于$x_i$的条件概率分布$\mathcal{P}(x_i\mid x_{-i})$同样服从高斯分布，对应高斯分布表示如下：
  $x_{-i}$表示随机变量集合$\mathcal{X}$中除去$x_i$之外的其他随机变量。
  $$\forall x_i,\mathcal{P}(x_i\mid x_{-i})\sim \mathcal{N}(\sum _{j\ne i}\frac{{\lambda }_{ij}}{{\lambda }_{ii}}{x}_j,{\lambda }_{ii}^{-1})$$
  这个思想和高斯分布推断任务中的已知联合概率分布$\mathcal{P}(\mathcal{X})=\mathcal{P}(x_{\mathcal{A}},x_{\mathcal{B}})$，求解条件概率分布$\mathcal{P}(x_{\mathcal{A}}\mid x_{\mathcal{B}})$完全一致。只不过这里将随机变量集合划分成两部分：

  • $x_i$单独一部分；
  • 除去$x_i$之外的其他随机变量为一部分。
    这里不推导了~

  观察上式的均值部分：如果${\lambda }_{ij}=0$，对应均值结果针对$x_j$的项为0。至此，剩余的结果如：
  这里只是举个例子，至少有一个特征$x_k$的对应结果不为0，这意味着$x_k$和$x_i$之间存在边。
  $$\sum _{j\ne i}\frac{{\lambda }_{ij}}{{\lambda }_{ii}}{x}_j=0+\cdots +\frac{{\lambda }_{ik}}{{\lambda }_{ii}}{x}_k+0+\cdots +0$$
  因此，可以将$x_i$看作与其相连的$x_j$的线性组合，这些结点在马尔可夫随机场结构表示中介绍过，被称作马尔可夫毯(Markov Blanket)。

至此，高斯网络部分介绍结束。

相关参考：
机器学习-高斯网络(3)-高斯马尔可夫随机场