【sklearn学习】线性回归LinearRegression
多元线性回归指一个样本中有多个特征的线性回归问题
sklearn.linear_model.LinearRegression
class sklearn.linear_model.LinearRegression(*, fit_intercept=True, normalize='deprecated', copy_X=True, n_jobs=None, positive=False)
- fit_intercept:默认为True,计算模型的截距
- normalize 默认是False,如果为True,训练样本会在回归之前被归一化
- copy_X 默认为True,否则特征矩阵被线性回归影响并覆盖
- n_jobs:用于计算的作业数,-1表示使用所有cpu
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import RidgeCV
from sklearn.linear_model import Lasso
from sklearn.datasets import load_boston
import warnings
warnings.simplefilter("ignore")boston = load_boston()
df_data = pd.DataFrame(boston.data)
df_data.columns = boston.feature_names
df_target = pd.DataFrame(boston.target)
df_target.columns = ['LABEL']
df = pd.concat([df_data, df_target], axis=1)线性回归方法:
X_train, X_test, y_train, y_test = train_test_split(df_data, df_target, test_size=0.2, random_state=0)
linR = LinearRegression()
linR.fit(X_train, y_train)
train_score = linR.score(X_train, y_train)
test_score = linR.score(X_test, y_test)
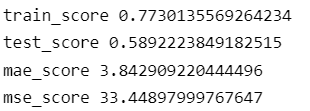
print('train_score',train_score)
print('test_score',test_score)
y_pred = linR.predict(X_test)
mae_score = mean_absolute_error(y_pred, y_test)
mse_score = mean_squared_error(y_pred, y_test)
print('mae_score',mae_score)
print('mse_score',mse_score)
k折交叉验证的线性回归:
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
data_train, data_test, target_train, target_test = train_test_split(df_data, df_target['LABEL'], test_size=0.2, random_state=0)
folds = KFold(n_splits=10)
train_scores = 0
val_scores = 0
mae_scores = 0
mse_scores = 0
for fold, (train_index, val_index) in enumerate(folds.split(data_train, target_train)):
print("fold {}".format(fold+1))
X_train, X_val, y_train, y_val = data_train.values[train_index],data_train.values[val_index],target_train.values[train_index],target_train.values[val_index]
linR = LinearRegression()
linR.fit(X_train, y_train)
train_score = linR.score(X_train, y_train)
val_score = linR.score(X_val, y_val)
print('train_score',train_score)
print('val_score',val_score)
y_pred = linR.predict(X_val)
mae_score = mean_absolute_error(y_pred, y_val)
mse_score = mean_squared_error(y_pred, y_val)
train_scores += train_score
val_scores += val_score
mae_scores += mae_score
mse_scores += mse_score
print('train_score',train_score)
print('val_score',val_score)
print('mae_score',mae_score)
print('mse_score',mse_score)
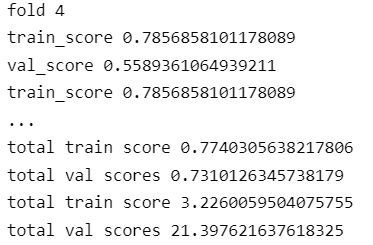
print("total train score",train_scores/10)
print("total val scores",val_scores/10)
print("total train score",mae_scores/10)
print("total val scores",mse_scores/10)
test_score = linR.score(data_test, target_test)
y_test_pred = linR.predict(data_test)
mae_score = mean_absolute_error(y_test_pred, target_test)
mse_score = mean_squared_error(y_test_pred, target_test)
print('test_score',test_score)
print('mae_score',mae_score)
print('mse_score',mse_score)可视化预测结果:
plt.figure(figsize=(20,5),dpi=80)
x = np.arange(0,50,1)
y = y_test[0:50]
z = y_pred[0:50]
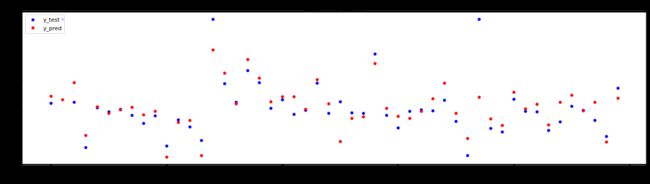
plt.scatter(x, y, s=20, color='blue', label='y_test')
plt.scatter(x, z, s=20, color='red', label='y_pred')
# 添加描述信息
plt.xlabel('index')
plt.ylabel('value')
plt.title('y_test and y_pred')
plt.legend(loc='upper left')
plt.show()
岭回归与Lasso
多重共线性,当不是满秩矩阵时存在多个解析解,都能使均方误差最小化,常见方法使引入正则化项,所谓正则化,就是对模型的参数添加一些先验假设,控制模型空间,以达到使得模型复杂度较小的目的。岭回归和Lasso是目前最为流行的两种线性回归正则化方法。
岭回归
通过在损失函数中加入L2范数惩罚项,来控制线性模型的复杂程度,从而使模型更稳健。
sklearn.linear_model.Ridge
class sklearn.linear_model.Ridge(alpha=1.0, *, fit_intercept=True, normalize='deprecated', copy_X=True, max_iter=None, tol=0.001, solver='auto', positive=False, random_state=None)
solver{‘auto’, ‘svd’, ‘cholesky’, ‘lsqr’, ‘sparse_cg’, ‘sag’, ‘saga’, ‘lbfgs’}, default=’auto’
alpha:α值,值越大则正则化的占比越大
fit_intercept:bool,是否需要计算b值,如果为false,那么不计算b值,模型假设数据已经中心化
max_iter:指定最大迭代次数
normalize:bool,如果为True,训练样本会在回归之前被归一化
solver:字符串,指定求解最优化问题的算法
auto:根据数据集自动选择算法
svd:使用奇异值分解来计算回归系数
cholesky:使用scipy.linalg.solve函数来求解
如果一个数据集在岭回归中使用各种正则化参数取值下模型没有明显上升,则说明数据没有多重共线性;反之,如果一个数据集在岭回归的各种正则化参数取值下表现出明显上升的趋势,则说明数据存在多重共线性。
sklearn.linear_model.RidgeCV
class sklearn.linear_model.RidgeCV(alphas=(0.1, 1.0, 10.0), *, fit_intercept=True, normalize='deprecated', scoring=None, cv=None, gcv_mode=None, store_cv_values=False, alpha_per_target=False)[source]¶
alphas:需要测试的正则化参数的取值的元组
scoring:用来进行交叉验证的模型评估指标
cv:交叉验证的模式,默认使留一交叉验证
srore_cv_values:是否保存每次交叉验证的结果
alpha_:查看交叉验证选中的alpha
cv_values_:调用所有交叉验证的结果
Ridge_model = Ridge()
Ridge_model.fit(data_train, target_train)
train_score = Ridge_model.score(data_train, target_train)
print('train score:',train_score)
test_score = Ridge_model.score(data_test, target_test)
print('test score:',test_score)Lasso与多重共线性
Lasso回归和岭回归的区别在于它的惩罚项是基于L1范数,可以将系数控制收缩到0,从而达到变量选择的效果。
sklearn.linear_model.Lasso
class sklearn.linear_model.Lasso(alpha=1.0, *, fit_intercept=True, normalize='deprecated', precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')
selection:{'positive', 'cyclic'}
Lasso_model = Lasso()
Lasso_model.fit(data_train, target_train)
train_score = Lasso_model.score(data_train, target_train)
print('train score:',train_score)
test_score = Lasso_model.score(data_test, target_test)
print('test score:',test_score)sklearn.linear_model.LassoCV
class sklearn.linear_model.LassoCV(*, eps=0.001, n_alphas=100, alphas=None, fit_intercept=True, normalize='deprecated', precompute='auto', max_iter=1000, tol=0.0001, copy_X=True, cv=None, verbose=False, n_jobs=None, positive=False, random_state=None, selection='cyclic')
eps:正则化路径的长度
n_alphas:正则化路径中α的个数
alphas:需要测试的正则化参数的取值的元组
cv:交叉验证的次数