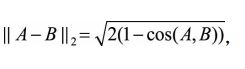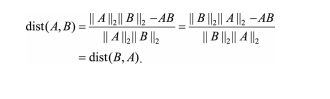百面机器学习

数学与智力题

线性代数

如何直观理解矩阵和线性代数？

行列式

行列式的本质是什么？

矩阵运算

关于矩阵的知识点梳理

大佬的矩阵求导合集

深度神经网络中的BP算法矩阵求导

线性回归与Logistic回归的矩阵求导

线性回归与Logistic回归的矩阵求导（续）

概率论与数理统计

排列组合

概率计算

• 一根绳子被切两刀能组成一个三角形的概率

列方程与约束条件，几何概型

$\frac{1}{4}$

• 一段绳子切n刀，组成n+1边型

考虑无法组成（某段长度>$\frac{1}{2}$）

$1-\frac{n+1}{2^n}$

• 抛硬币多少次才连续两次正面朝上

几何分布期望的泛化

$E(p)=\frac{1}{p}+\frac{1}{p^2}+\cdots$

• 圆上取3点组成锐角三角形

1. 测度法。1个锐角三角形对应3个钝角，所以是$\frac{1}{1+3}$
2. 积分法。固定两点然后${\int }_0^{\pi }\frac{\alpha }{2\pi }\cdot \frac{1}{\pi }d\alpha =\frac{1}{4}$

• 分配白球和红球，取到红球概率

• 递归求期望

• 地区每天下雨的概率是0.8，天气预报准确性为0.8

• 在一个球面任取4个点，请问这4个点构成的4面体会经过球心的概率

$\frac{1}{8}$

• 一个半径为1的圆周上有三个点，求三个点构成的图形的面积的期望值？

$\frac{3}{2\pi }$

字节跳动面试题.个人玩抛硬币的游戏，谁先抛到正面就获胜。那么先抛的人获胜概率为？

数理统计

常见分布：

https://blog.csdn.net/Ga4ra/article/details/78935537

期望与方差的推导：

https://zhuanlan.zhihu.com/p/30496723

智力题

• 博弈论

取物游戏的必胜策略

1. 特征工程

归一化

MinMax

Z-Score

x1x2更新速度变得一致，更容易找到梯度下降的最优解

需要归一化：线性回归、 逻辑回归、 支持向量机、 神经网络
不需要归一化：决策树模型

决策树在进行节点分裂时主要
依据数据集D关于特征x的信息增益比（详见第3章第3节） ， 而信息增益比跟特征
是否经过归一化是无关的

类别特征编码

序号编码（ Ordinal Encoding） 、 独热编码（ One-hot Encoding） 、 二进制编码
（ Binary Encoding）

高维组合特征的处理

会把一阶离散特征两两组合， 构成高阶组合特征。

一种行之有效的方法是将用户和物品分别用k维的低维向量表示（ k<

组合特征

怎样有效地找到组合特征？

基于决策树的特征组合寻找方法

文本表示模型

• 词袋模型（ Bag of Words）
• TF-IDF（ Term Frequency-Inverse Document Frequency）
• 主题模型（ Topic Model）
• 词嵌入模型（ Word Embedding）

词嵌入是一类将词向量化的模型的统称， 核心思想是将每个词都映射成低维空间（ 通常K=50～300维） 上的一个稠密向量（ Dense Vector） 。

Word2Vec

Word2Vec实际是一种浅层的神经网络模型， 它有两种网络结构， 分别是CBOW（ Continues Bagof Words） 和Skip-gram。

Word2Vec是如何工作的？ 它和LDA有什么区别与联系？

• CBOW的目标是根据上下文出现的词语来预测当前词的生成概率
• 而Skip-gram是根据当前词来预测上下文中各词的生成概率

LDA是利用文档中单词的共现关系来对单词按主题聚类， 也可以理解为对“文档-单词”矩阵进行分解， 得到“文档-主题”和“主题-单词”两个概率分布。

而Word2Vec其实是对“上下文-单词”矩阵进行学习， 其中上下文由周围的几个单词组成， 由此得到的词向量表示更多地融入了上下文共现的特征。

2. 模型评估

RMSE

很好地反映回归模型预测值与真实值的偏离程度。 但在实际问题中， 如果存在个别偏离程度非常大的离群点（ Outlier） 时， 即使离群点数量非常少， 也会让RMSE指标变得很差。

MAPE相当于对误差进行了归一化，降低了个别离群点带来的绝对误差影响

P R

精确率与召回率的权衡。

hulu视频精确率与召回率的平衡

如果相关结果有100个， 即使Precision@5达到了100%， Recall@5也仅仅是5%。

模型的P-R（ PrecisionRecall） 曲线

F1是两者的调和平均（harmonic mean）

$F_{\beta }$

https://en.wikipedia.org/wiki/F-score

Two commonly used values for β are 2, which weighs recall higher than precision, and 0.5, which weighs recall lower than precision.

$\beta$越大（如2），recall越重要。$\beta$越小（如0.5），precision越重要。

Micro-Macro Average

• 宏平均的计算方法独立于不同类别，将每个类别的 P、R、F 值单独计算出来，然后将所有类别的度量值直接平均，因此它将各个类别平等对待。

• 而微平均会结合不同类别的贡献大小来计算平均值。

所以，在多分类问题中，如果存在数据不均衡问题，则使用微平均得到的效果会更加可信！

Micro Average vs Macro average Performance in a Multiclass classification setting

ROC-AUC

ROC曲线是Receiver Operating Characteristic Curve的简称

横坐标为假阳性率（ False Positive Rate， FPR） ； 纵坐标为真阳性率（ True Positive Rate， TPR） 。

为什么ROC曲线不受样本不均衡问题的影响

TPR考虑的是第一行，实际都是正例，FPR考虑的是第二行，实际都是负例。因此，在正负样本数量不均衡的时候，比如负样本的数量增加到原来的10倍，那TPR不受影响，FPR的各项也是成比例的增加，并不会有太大的变化。因此，在样本不均衡的情况下，同样ROC曲线仍然能较好地评价分类器的性能，这是ROC的一个优良特性。

更直观地绘制ROC曲线的方法

根据样本标签统计出正负样本的数量， 假设正样本数量为P， 负样本数量为N；

把横轴的刻度间隔设置为1/N， 纵轴的刻度间隔设置为1/P； 再根据模型输出的预测概率对样本进行排序（ 从高到低） ；

依次遍历样本， 同时从零点开始绘制ROC曲线， 每遇到一个正样本就沿纵轴方向绘制一个刻度间隔的曲线， 每遇到一个负样本就沿横轴方向绘制一个刻度间隔的曲线， 直到遍历完所有样本， 曲线最终停在（ 1,1） 这个点， 整个ROC曲线绘制完成。

AUC值只需要沿着ROC横轴做积分就可以了。

AUC越大， 说明分类器越可能把真正的正样本排在前面， 分类性能越好。

ROC曲线有一个特点， 当正负样本的分布发生变化时， ROC曲线的形状能够基本保持不变， 而P-R曲线的形状一般会发生较剧烈的变化。

ROC曲线能够尽量降低不同测试集带来的干扰， 更加客观地衡量模型本身的性能。

有效计算ROC-AUC的方法

import numpy as np
from sklearn.metrics import roc_auc_score

def auc(labels, probs):
    n_samples = len(labels)
    pos_cnt = sum(labels)
    neg_cnt = n_samples - pos_cnt
    
    total_comb = pos_cnt * neg_cnt #组合数
    
    pos_index = np.where(labels==1)[0] #找出正例的索引
    neg_index = np.where(labels==0)[0] # 找出负例的索引
    
    cnt = 0
    for pos_i in pos_index:
        for neg_j in neg_index:
            if probs[pos_i] > probs[neg_j]:
                cnt += 1
            elif probs[pos_i] == probs[neg_j]:
                cnt += 0.5
            else:
                cnt += 0
    auc = cnt / total_comb
    return auc

labels = np.array([1,1,0,0,1,1,0])
probs= np.array([0.8,0.7,0.5,0.5,0.5,0.5,0.3])
print('ours:', auc(labels,probs))
print('sklearn:', roc_auc_score(labels,probs))

余弦距离

如果希望得到类似于距离的表示， 将1减去余弦相似度即为余弦距离。 因此， 余弦距离的取值范围为[0,2]， 相同的两个向量余弦距离为0。

在一些场景， 例如Word2Vec中， 其向量的模长是经过归一化的， 此时欧氏距离与余弦距离有着单调的关系， 即

随便推一下就知道了

在此场景下， 使用余弦相似度和欧氏距离的结果是相同的。

欧氏距离体现数值上的绝对差异， 而余弦距离体现方向上的相对差异。

余弦距离是否是一个严格定义的距离？

• 正定性

余弦距离的取值范围是[0, 2]

• 对称性

• 三角不等式

KL距离不满足三角不等式

模型评估的方法

超参数调优

贝叶斯优化算法则充分利用了之前的信息。 贝叶斯优化算法通过对目标函数形状进行学习， 找到使目标函数向全局最优值提升的参数。

具体来说， 它学习目标函数形状的方法是， 首先根据先验分布， 假设一个采集函数； 然后， 每一次使用新的采样点来测试目标函数时， 利用这个信息来更新目标函数的先验分布； 最后， 算法测试由后验分布给出的全局最值最可能出现的位置的点。

过拟合和欠拟合

过拟合就是学习噪声

降低过拟合的方法：

• 获取更多的训练数据
• 降低模型复杂度
• 正则化方法
• 集成学习方法

降低欠拟合的方法：

• 添加新特征（FM， GBDT， DeepCrossing）
• 增加模型复杂度
• 减少正则化系数

机器学习基础

偏差方差分解

偏差	方差
不同训练集上的平均性能与最优模型的差异	一个模型在不同训练集上的差异
模型的拟合能力	模型是否容易过拟合

集成模型，即通过多个高方差模型的平均来降低方差

1、bias与variance的含义，并结合ensemble method问哪种方法降低bias，哪种方法降低variance

机器学习中的 Bias（偏差）、Error（误差）、Variance（方差）有什么区别和联系？

bias描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距
varience描述的是样本上训练出来的模型在测试集上的表现

而generalization error又可以细分为Bias和Variance两个部分。
Bias是 “用所有可能的训练数据集训练出的所有模型的输出的平均值” 与 “真实模型”的输出值之间的差异；
Variance则是“不同的训练数据集训练出的模型”的输出值之间的差异。

为什么说bagging是减少variance，而boosting是减少bias?

• bagging
  • 由于$E[\frac{\Sigma X}{n}]=E[X]$，所以bagging后的bias和单个子模型的接近，一般来说不能显著降低bias。
  • 另一方面，若各子模型独立，则有$\mathrm{Var}\left(\frac{\sum X_i}{n}\right)=\frac{\mathrm{Var}\left(X_i\right)}{n}$，此时可以显著降低variance。
• boosting
  • 各个基模型是强相关的，所以variance不变

结合Ensemble Method谈谈Bias和Variance的含义

理论和定理

PAC学习理论

可能近似正确（ProbablyApproximately Correct，PAC）学习理论．

因为训练样本有限，所以希望从有限样本中学习到期望错误为0的fx是不切实际的。因此，需要降低对学习算法能力的期望，只要求学习算法可以以一定的概率学习到一个近似正确的假设，即PAC学习（PAC Learning）．

一个PAC可学习（PAC-Learnable）的算法是指该学习算法能够在多项式时间内从合理数量的训练数据中学习到一个近似正确的()．

TODO： 看懂

没有免费午餐定理

任何算法都有局限性．必须要“具体问题具体分析”．

奥卡姆剃刀原理

TODO： 学习 最小描述长度 原则

---

• 丑小鸭定理

归纳偏置

在机器学习中，很多学习算法经常会对学习的问题做一些假设，这些假设就称为归纳偏置（Inductive Bias）

• 最近邻分类器中，我们会假设在特征空间中，一个小的局部区域中的大部分样本同属一类．
• 在朴素贝叶斯分类器中，我们会假设每个特征的条件概率是互相独立的．

在贝叶斯学习中也经常称为先验（Prior）．

3. 经典算法

线性回归

※ 线性回归面经总结——from 牛客

---

闭式解

「05」回归的诱惑：一文读懂线性回归

如果问L对w的导数是多少？w的close form解是多少？首先想到这个：

右边是误差，左边是Xw对X求导

然后稍微算一下就知道w的闭式解是多少了

如果特征间存在共线性，或者特征数>样本数，会导致上式的$X^{T}X$不可逆

不可逆的情况下会存在很多解 $w$

还有一种解决方案是加L1正则，满秩，行列式不为0

最大似然估计 MLE

线性回归损失函数为什么要用平方形式

在误差服从正态分布的前提下，与极大似然估计的思想在本质上是相同。

理解：频率派角度-误差复合高斯分布的最大似然估计

最大似然估计：从概率角度理解线性回归的优化目标

求法：

1. 误差服从$N(0,\sigma )$=> y服从$N(wx,\sigma )$
2. 用高斯概率密度函数表示出y，然后进行极大似然估计

用高斯概率密度函数表示出y的分布 (当前xw取值下y的概率，误差越小概率越大)

前面的推导中发现，最小二乘与最大似然的公式几乎一样。直观上来说，最小二乘法是在寻找观测数据与回归超平面之间的误差距离最小的参数。最大似然估计是最大化观测数据发生的概率。当我们假设误差是正态分布的，所有误差项越接近均值0，概率越大。正态分布是在均值两侧对称的，误差项接近均值的过程等同于距离最小化的过程。

最大似然估计是机器学习中最常用的参数估计方法之一，逻辑回归、深度神经网络等模型都会使用最大似然估计。我们需要一个似然函数来描述真实数据在不同模型参数下发生的概率，似然函数是关于模型参数的函数。最大似然估计就是寻找最优参数，使得观测数据发生的概率最大、统计模型与真实数据最相似。

如何通俗地理解概率论中的「极大似然估计法」?

这种通过事实，反过来猜测硬币的情况，就是似然。

$W={\left(X^{T}X\right)}^{-1}{X}^{T}Y$

$W=(X^{T}X+\lambda I{)}^{-1}{X}^{T}Y$

从两个角度理解：

• 频率角度：维度太大无法求逆矩阵，且容易过拟合，给w加上约束:$(X^{T}X+\lambda I{)}^{-1}$是半正定，不一定可逆，$(X^{T}X+\lambda I{)}^{-1}$为半正定加单位矩阵，是正定的，可逆
• 贝叶斯角度（最大后验）：参数符合laplace分布>L1正则，符合高斯分布>L2岭回归

最大后验估计 MAP

为了避免过拟合，我们可以给参数加上一些先验知识

贝叶斯估计是一种参数的区间估计，即参数在一个区间上的分布

希望得到一个最优的参数值（即点估计），可以使用最大后验估计．

LR

SVM

决策树

决策树有哪些常用的启发函数？

• ID3 最大信息增益
• C4.5 最大信息增益比
• CART 基尼指数

剪枝方法

• 预剪枝
  • 树达到一定深度的时候，停止树的生长
  • 某结点样本数量小于阈值
  • 信息增益的提升
• 后剪枝
  • CCP 代价复杂度剪枝 Cost Complexity Pruning

4. 降维

PCA

PCA旨在找到数据中的主成分， 并利用这些主成分表征原始数据， 从而达到降维的目的。

可以从最小平方误差和最大方差的角度进行解释。

5. 非监督学习

6. 概率图模型

贝叶斯网络（ Bayesian Network） ：有向图模型，CRF

马尔可夫网络（ Markov Network）：无向图模型，HMM

有空看下喆神的推导

解释朴素贝叶斯模型的原理， 并给出概率图模型表示

后验概率$P(X|y_i)$决定了分类的结果

和上面的贝叶斯网络对比一下，就知道了

解释最大熵模型的原理， 并给出概率图模型表示。

有空看一下

7. 优化算法

Momentum引入了动量v，以指数衰减的形式累计历史梯度，以此来解决Hessian矩阵病态问题

Nesterov是对Momentum的变种。与Momentum不同的是，Nesterov先更新参数，再计算梯度

• 每个参数有不同的学习率：
  • AdaGrad 学习率逐参数的除以历史梯度平方和的平方根
  • RMSProp 历史梯度平方和$\to$指数衰减的移动平均,以此丢弃遥远的过去历史。
  • Adam Adam算法可以看做是修正后的Momentum+RMSProp算法

从 SGD 到 Adam —— 深度学习优化算法概览(一)
Adam 究竟还有什么问题 —— 深度学习优化算法概览(二)

有空看看这个，有些结论：

Deep Learning 最优化方法之SGD

损失函数

经典的优化算法

L1正则化与稀疏性

8. 采样

9. 前向神经网络

10. 循环神经网络

12. 集成学习

2、lr与svm的区别与联系

LR和SVM的联系区别

3、gbdt与adaboost的区别与联系
4、手推svm，svm麻雀虽小五脏俱全
5、pca与lda的区别与联系，并推导
6、白化的原理与作用
7、给一个算法，例如lr，问这个算法的model、evaluation、optimization分别是啥