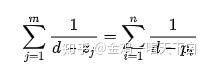matlab求系统根轨迹代码_第九讲? 根轨迹法

金鸡一唱天下白：第八讲 系统的时域响应​zhuanlan.zhihu.com

自动化人 - 知乎​www.zhihu.com

反馈系统（线性时不变系统）的稳定性由其闭环极点唯一确定。反馈系统的闭环极点就是该系统特征方程的根。最简单的判稳方法是求特征方程的特征根，如果所有特征根都是负的，那么系统肯定是稳定的。对于一阶、二阶系统而言，很简单，用求根公式解出来就行了；但是，对于高阶系统，如三阶、四阶的，用求根公式的方法行不通，求根过程会变得十分复杂，特别是在系统参数变化情况下求根，更是需要进行大量的运算，而且还不宜直观看出参数变化对系统闭环极点分布的影响。有鉴于此，1948年，伊凡思(W.R.Evans)提出了一种图解反馈系统特征方程的工程方法，该法称为根轨迹法。

它不直接求解特征方程,而用图解法来确定系统的闭环特征根。所谓根轨迹就是系统的某个参数连续变化时，闭环特征根在复平面上画出的轨迹，也就是是开环系统某一参数从零变化到无穷时，闭环特征根在复平面[s]上变化的轨迹。如果这个参数是开环增益，在根轨迹上就可以根据已知的开环增益找到相应的闭环特征根，也可以根据期望的闭环特征根确定开环增益。

传递函数的零极点表示，根轨迹的概念，根轨迹的基本条件，根轨迹的基本规则，等效开环传递函数的概念，根轨迹定性分析系统性能指标随系统参数变化的趋势，确定系统闭环零极点及系统性能指标。

线性时不变系统的动态性能主要取决于闭环系统特征方程的根（闭环极点），所以控制系统的动态设计，关键就是合理地配置闭环极点。调整开环增益是改变闭环极点的常用办法。

一、基本概念

1. 什么是根轨迹

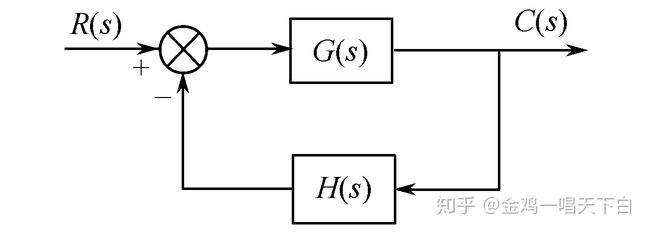
图9-1 负反馈控制系统

假如有如图9-1所示负反馈控制系统，设其开环传递函数为：

则该系统的闭环特征方程为：

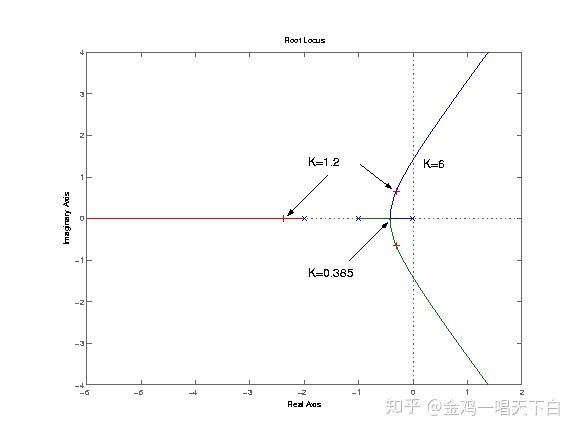
当K从零到无穷大连续变化时，闭环极点S在平面（复平面）上画出的根轨迹如图9-2所示。

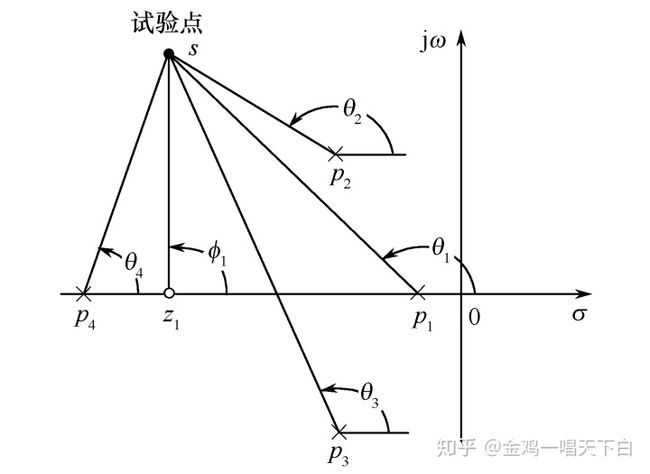
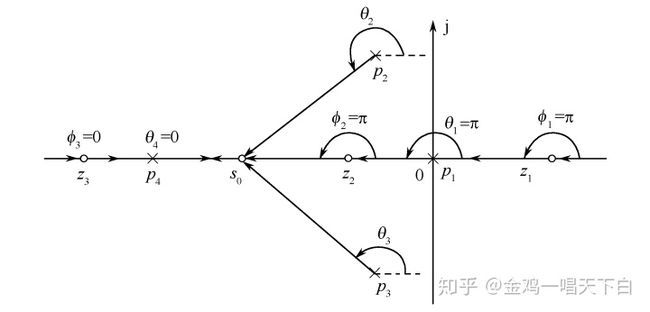
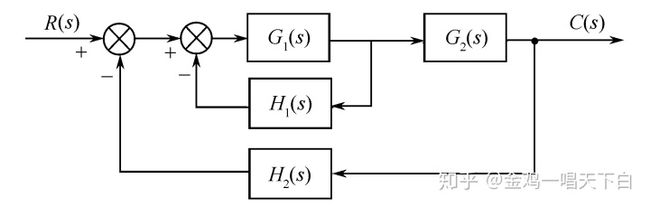
图9-2 根轨迹

从上面的根轨迹图，我们可以看出：当00.385时，有两个闭环极点成为共轭复数，只要0

根轨迹法就是在已知每个给定反馈系统的开环极点与零点分布基础上，通过系统参数K的变化图解特征方程，即根据参数变化研究系统闭环极点分布的一种图解法。

2.相角条件

我们首先讨论根轨迹最基本最重要的规律——相角条件。考察图9-1所示的系统，其闭环传递函数为:

闭环特征方程为：

上式可分为幅值条件:

和相角条件：

在S复平面上，给定了幅值和相角，就对应一个固定的点，所以既满足幅值条件又满足相角条件的S值就是特征方程的一组根，也就是一组闭环极点。

根轨迹法研究系统的一个可调参数对闭环极点的影响，最常见的可调参数是开环增益K。令G(s)=KG0(s)，显然，K的变动只影响幅值条件不影响相角条件，也就是说，根轨迹上的所有点满足同一个相角条件，K变动相角条件是不变的。所以，绘制根轨迹可以这样进行：首先在S平面上找出所有符合相角条件的点，这些点连成的曲线就是根轨迹，然后反过来按幅值条件求出根轨迹上任一点的K值。

二、绘制典型根轨迹

我们可以把现有的绘制根轨迹图的方法分为三类：

1）手工画概略图（草图）。这种方法适合调试现场的应急分析、项目开始的粗略分析等不要求很精确的场合。一个熟习根轨迹基本规则的人几分钟就可以画出一张很有用的概略图。

2）手工图解加计算画准确图。这种方法曾经沿用很久，以往的教科书讲述了很多绘图的技艺，不仅繁琐，精度也差，这类方法在实际应用中已逐步淘汰。

3）计算机绘制精确图，目前主要指用Matlab工具绘制根轨迹图。它准确快捷，短时间内可以对多个可调参数进行研究，有效地指导设计与调试。

1.开环零极点与相角条件

我们这里讨论的是以开环增益K为参变量的根轨迹，它是最基本、最常用的根轨迹，为了区别，我们称之为‘典型根轨迹’。仍然针对图4-1所示负反馈系统，设系统开环传递函数可以表示为：

式中p1,p2,…pn，为开环极点，z1,z2,…zm 为开环零点。这样，系统的闭环特征方程可以表示为：

以K为参变量的根轨迹上的每一点都必须满足该方程，相应地，我们称之为‘典型根轨迹方程’。上式也可以写成(消去分母)：

这时，幅值条件具体化为：

相角条件具体化为：

按相角条件绘制根轨迹图的依据。具体方法是：在复平面上选足够多的试验点，对每一个试验点检查它是否满足相角条件，如果是则该点在根轨迹上，如果不是则该点不在根轨迹上，最后将在根轨迹上的试验点连接就得到根轨迹图。以下列4阶系统为例：

先在复平面上标出开环极点p1,p2,p3,p4和开环零点z1如图9-3。对试验点S，如果它在根轨迹上，就应当满足相角条件 ：

量出或计算出5个角度，就知道试验点s是否在根轨迹上。判别了一个试验点，再判别其它试验点．．．．。

图9-3

为了尽快把握绘制根轨迹的要领，请牢记并理解三句话：绘制根轨迹——依据的是开环零极点分布，遵循的是不变的相角条件，画出的是闭环极点的轨迹。

2.基本规则

纯粹用试验点的办法手工作图，工作量是十分巨大的，而且对全貌的把握也很困难，于是人们研究根轨迹图的基本规则，以便使根轨迹绘图更快更准。概括起来， 以开环增益K为参变量的根轨迹图主要有下列基本规则：

1）起点和终点

根轨迹一定开始于开环极点，终止于开环零点。

因为根轨迹是闭环特征方程的根，当K=0时方程的根就是它的n个开环极点，当K→∞时方程的根就是它的m个开环零点。根轨迹的起点和终点是根轨迹的特殊点。当n=m时，开始于n个开环极点的n支根轨迹，正好终止于 个开环零点。

当n>m时，开始于n个开环极点的n支根轨迹，有m支终止于开环零点，有n-m支终止于无穷远处。用式（4-9）可以解释这一规则：终点就是K→∞的点，要K→∞只有两种情况，一是s=zl(l=1,2,…,m)，二是s→∞。这时，无穷远处也称为‘无穷远零点’。

当n时，终止于m个开环零点m支根轨迹，有 支来自个开环极点，有m-n支来自无穷远处。必需指出，实际系统极少有n的情况，但是在处理特殊根轨迹时，常常将系统特征方程变形，变形后的等价系统可能会出现这种情况（参见§3.3）。

2）分支数和对称性

根轨迹一定对称于实轴，并且有max(n,m)支。

因为根轨迹是闭环特征方程的根，无论K如何变化特征方程始终有max(n,m)个根，即使出现重根，当K从零到无穷大连续变化时重根不可能始终为重根，所以根轨迹一定有max(n,m)支。

特征方程的根要么是实根（在实轴上）要么是共轭复根（对称于实轴），所以根轨迹一定对称于实轴。

3）实轴上的根轨迹

实轴上的开环零点和开环极点将实轴分为若干段，对于其中任一段，如果其右边实轴上的开环零、极点总数是奇数，那么该段就一定是根轨迹的一部分。

图9-4

这个规则用相角条件可以证明。考虑实轴上的某一试验点s0（见图9-4所示），任意一对共轭开环零点或共轭极点（如p2,p3）对应的相角（如θ2,θ3）之和均为360度。也就是说任一对共轭开环零、极点不影响实轴上试验点s0的相角条件。再看实轴上的开环零、极点，对试验点s0 ，其左边实轴上任一开环零、极点对应的相角（如θ4,φ3）均为0，其右边实轴上任一开环零、极点对应的相角（如θ1,φ1,φ2）均为180度。所以要满足相角条件，s0右边实轴上的开环零、极点总数必须是奇数。

4）渐近线

根轨迹的渐近线。当开环有限极点数n大于有限零点数m时，有n-m条根轨迹分支沿着与实轴交角为

，交点为

的一组渐近线趋向无穷远处，且有

5）会和分离点与分离角

会和分离点的意思就是根轨迹会在这里会和和分离，也就是说有重根。两条或两条以上根轨迹分支在s平面上相遇又立即分开的点，称为根轨迹的分离点，分离点的坐标d是下列方程的解：

式中，zj为各开环零点的数值；pi为各开环极点的数值；分离角为（2k+1）π/l

6）起始角与终止角

根轨迹的起始角与终止角。只有当出现复数零极点时，才会考虑用此规则！根轨迹离开开环复数极点处的切线与正实轴的夹角，称为起始角；根轨迹进入开环复数零点处的切线与正实轴的夹角，称为终止角。这两个角度都是通过相角条件求的。

相角条件？n-m>2时

分子的角度之和减去分母的角度之和=（2K+1）*pai（180度根轨迹）

就是零点的角度之和减去极点的角度之和。

那么，接下来在列式子时，只需要将同类型的角度放在一块就好了。这样就可以避免出错！

7）与虚轴的交点

根轨迹与虚轴的交点。若根轨迹与虚轴相交，则交点上的值和ω值可用劳斯判据确定，也可令闭环特征方程中的s=jω，然后分别令其实部和虚部为零而求得。

8）根之和

n-m>2时：开环极点之和=闭环极点之和。

下面举一个例子：

控制系统如上图所示。其开环传递函数为:

利用计算结果在S平面上描点并用平滑曲线将其连接，便得到K * （或K）从零变化到无穷大时闭环极点在S平面上移动的轨迹，即根轨迹，如下图所示。图中，根轨迹用粗实线表示，箭头表示K * （或K）增大时两条根轨迹移动的方向。

三、用MATLAB绘制根轨迹图

使用用Matlab软件绘制根轨迹图十分准确、快捷。现在用一个例子来说明用法。

考虑图9-1所示系统,设其中

用Matlab绘制根轨迹只要知道开环传递函数分子分母的系数，并分别填入分子向量num和分母向量den中，然后调用绘制根轨迹的专用函数rlocus就行了。对于本例，最简单的程序就是：

num=[ 1  2  4];
rlocus(num,den) 
den=[1  11.6  39  43.6  24  0];

在Matlab6.5的命令窗（Command Window）中执行这个程序，运行后就自动绘出根轨迹如图9-5所示，

图9-5

从根轨迹图可以看出：当0

四、控制系统的根轨迹分析

根轨迹图是设计和分析线性时不变控制系统的有力帮手，它揭示了稳定性、阻尼系数、振型等动态性能，用根轨迹图分析控制系统主要有以下方面：

根轨迹与稳定性

比如，当K在（0，∞）间取值时，如果n支根轨迹全部位于虚轴的左边，就意味着不管K取任何值闭环系统都是稳定的。反之，根轨迹只要有一支全部位于虚轴的右边，就意味着不管K取何值，闭环系统都不可能稳定，这种情况下，如果开环零、极点是系统固有的、不可改变的，那么要使系统稳定就必须人为增加开环零、极点，这就是通常讲的要改变系统的结构，而不仅仅是改变系统的参数。

根轨迹只要有一支穿越虚轴，就说明闭环系统的稳定是有条件的，知道了根轨迹与虚轴交点的K值，就可以确定稳定条件，进而确定合适的K值。

初学者容易把开环极点和闭环极点混淆，因为画根轨迹图时首先标在图上的是开环零、极点，根轨迹的起点是开环极点，有读者就误认为根轨迹上的点都是开环极点，这是不对的。根轨迹图上除了起点和终点，其它都是闭环极点的可能取值。

图9-6

但是，开、闭环又具有相对性，图9-6所示的是多环系统，对于内环，G1(s)H1(s)是开环传递函数，其极点是开环极点,φ1(s)=G1(s)/[1+G1(s)H1(s)] 是闭环传递函数，其极点是闭环极点；但是对于外环，φ1(s)G2(s)H2(s)是开环传递函数，其极点是外环的开环极点，φ1(s)的极点是外环开环极点的一部分。

可见，多环系统也可以用根轨迹进行分析，一般，首先依据G(s)H(s)的零、极点，绘制内环的根轨迹图，选择合适的K1使内环稳定；再依据φ1(s)G2(s)H2(s)的零、极点，绘制外环的根 轨迹图，选择合适的K2使外环稳定。

类似的问题还有开环稳定性和闭环稳定性，开环稳定的充要条件是开环极点都位于S平面的左半平面，开环稳定不意味着闭环稳定，开环不稳定也不意味着闭环不稳定，但是开环极点确实对闭环稳定有着重要影响——因为开环零、极点对根轨迹图有重要影响。

零、极点相消问题

在设计控制系统时，为了使系统阶次降低或者为了抵消大的惯性环节，有时用控制器的零（极）点去抵消被控对象的极（零）点，这在大多数情况下是有利的，但也有例外。

闭环零极点与时间响应

系统的动态性能最终体现在时间响应，影响时间响应的因素有两个：闭环传递函数和输入函数。在前面已经分析过：时间响应的暂态分量主要取决于闭环零、极点，时间响应的稳态分量主要取决于输入函数。

如前所说，闭环系统的稳定性完全取决于闭环极点，实际上时间响应的暂态分量也主要取决于闭环极点。每一个闭环极点si对应时间响应中的一个因子exp(sit)——称为系统的一个模态（Mode），si在S平面上的位置决定了它对应的暂态分量的运动形式。si分布于S平面上不同位置所对应的暂态分量，其规律可以总结为：

1)左右分布决定终值。具体讲就是： si位于虚轴左边时暂态分量最终衰减到零，si 位于虚轴右边时暂态分量一定发散， si正好位于虚轴（除原点）时暂态分量为等幅振荡。

2)虚实分布决定振型。具体讲就是：si位于实轴上时暂态分量为非周期运动，si位于虚轴上时暂态分量为周期运动。

3)远近分布决定快慢。具体讲就是：si位于虚轴左边时离虚轴愈远过渡过程衰减得愈快。所以离虚轴最近的闭环极点‘主宰’系统响应的时间最长，被称为主导极点。

设计系统时合理配置闭环极点是十分重要的，根据上述规律，一般首先配置主导极点，然后配置非主导极点，非主导极点与虚轴的距离应当是主导极点与虚轴距离的2～5倍，这样系统的时间响应就主要取决于一对主导极点。

主导极点一般安排为一对共轭复数极点，位于如图4-5虚轴左边60度扇形区内，且离虚轴有一定的距离，其理由在于：

1）闭环主导极点为共轭复数，使闭环系统的动态性能与一个二阶欠阻尼系统相似，二阶系统的动态性能是分析得最透彻的，欠阻尼系统则具有较快的反应速度。

2）阻尼系数太大太小都不合适，60度扇形区意味着阻尼系数不小于cos60°=0.5，一般认为最佳阻尼系数是0.707。

3）离虚轴一定的距离保证了足够的稳定裕度。稳定裕度太小，在实际应用时可能系统不稳定，因为数学模型的参数不会绝对准确——也就是说实际的主导极点位置与理论分析的位置有偏差。但也不是越远越好，因为系统总存在建模误差，离虚轴很远的极点对应很小的时间常数，如果主导极点与建模时忽略的小时间常数相当，那么主导极点就不‘主导’，设计的根基就动摇了。

说明

1、绘制反馈系统的根轨迹（包括180°根轨迹和0°根轨迹）只须依据相角条件，而幅值条件则用于计算根轨迹上某确定点对应的参变量值。

2、参变量并非一定为系统的开环增益，如参变量为系统开环增益或与之成比例，则此类根轨迹称为一般根轨迹；如参变量为开环系统某环节的时间常数，或系统时滞等，则此类根轨迹为参变量根轨迹。

综述：

根轨迹是系统的某个参数连续变化时，闭环特征根在复平面上画出的轨迹。绘制根轨迹可以总结为三句话：依据的是开环零极点分布，遵循的是不变的相角条件，画出的是闭环极点的轨迹。读者应重点掌握如何用基本规则1)—5)绘制概略图和用Matlab软件绘制精确图。借助于Matlab，控制系统的根轨迹分析变得更加灵活、透彻、高效。

根轨迹图揭示了稳定性、阻尼系数、振型等动态性能与系统参数的关系，用根轨迹图设计控制系统的关键是配置合适的闭环主导极点。要使理论设计符合工程实际，必须注意控制系统的鲁棒性。

金鸡一唱天下白：第十讲 典型环节的频域分析​zhuanlan.zhihu.com

自动化人 - 知乎​www.zhihu.com

注：版权属笔者所有，如需转载请务必联系！

最后说一句：码字不易，若此文对你有启发，收藏前请点个赞、点点喜欢，是对知乎主莫大的支持！！

参考

1.^文中内容或图片如有侵犯您的权益，请联系作者删除。