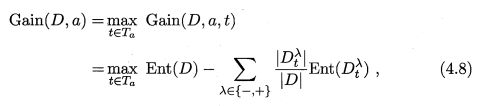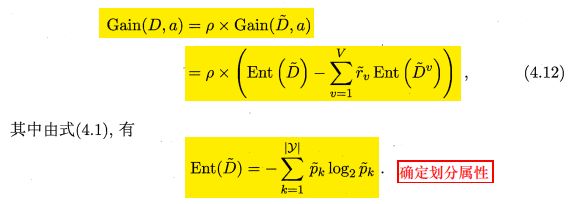机器学习(周志华、李航):决策树——算法原理及代码实现(持续更新)
文章目录
-
- 4.1 基本流程
-
- 决策树与条件概率分布
- 决策树学习
- 4.2 划分(特征)选择
-
- 4.2.1 信息增益
-
- 李书示例
- 周书示例
- 4.2.2 增益率
- 4.2.3 基尼指数
- 4.3 剪枝处理
-
- 4.3.1 预剪枝
- 4.3.2 后剪枝
- 4.4 连续与缺失值
-
- 4.4.1 连续值处理
- 4.4.2 缺失值处理
-
- 确定划分属性
- 操作
- 4.5 多变量决策树
- 4.6 CART 算法
-
- 4.6.1 CART 生成
-
- 1. 回归树生成
- 2. 分类树生成
- 4.6.2 CART 剪枝
- 代码实现
4.1 基本流程
决策树(decision tree):从给定数据集中学得一个模型用以对新示例进行分类。基于树结构进行决策。结点(node),有向边(directed edge)。
- 结点:内部结点(internal node 表示一个特征或属性);叶结点(leaf node 表示一个类)。
- 决策树分类:
- 从根结点开始,对实例的某一特征进行测试,根据测试结果将实例分配到其子结点;
- 每个子结点对应该特征的一个取值;
- 对所有实例递归地进行测试与分配,直至达到叶结点。最后将实例分到叶结点的类中。
学习时,利用训练数据,根据损失函数最小化原则建立决策树模型。预测时,对新的数据,利用决策树模型进行分类。通常包含3个步骤:特征选择、决策树生成、决策树修剪。
图示4.1:
决策过程中提出的每个判定问题都是对某个属性的“测试”。
- 决策树包含一个根结点、若干个内部结点和若干个叶子结点;
- 叶结点对应于决策结果,其他各结点对应于一个属性测试;每个结点包含的样本结合根据属性测试的结果被划分到子结点中;
- 根节点包含包含样本全集。从根结点到每个叶结点的路径对应了一个判定测试序列。
决策树学习的目的是产生一棵泛化能力强,处理未见示例能力强的决策树。 其流程遵循“分而治之(divide-and-conquer)”策略。
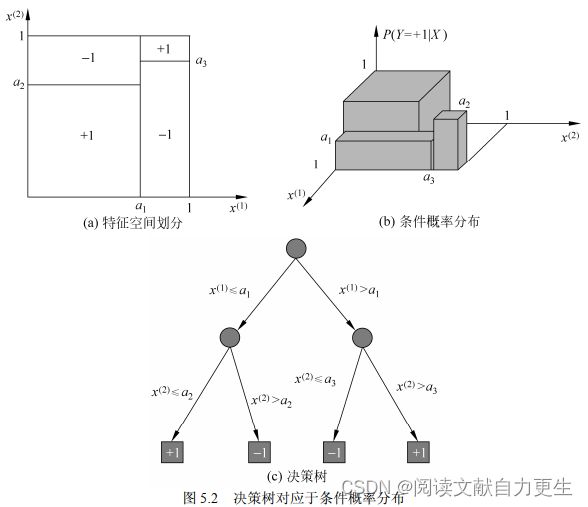
决策树与条件概率分布
决策树表示给定特征条件下类的条件概率分布。将特征空间划分为互不相交的单元(cell),在每个单元定义一个类的概率分布就构成了一个条件概率分布。决策树的一条路径对应划分中的一个单元。以 X X X 表示特征的随机变量, Y Y Y 表示类的随机变量,则条件概率分布表示为: P ( Y ∣ X ) P(Y|X) P(Y∣X)。
各叶结点(单元)上的概率分布偏向某一个类,属于某个类的概率大,决策树分类将该结点的实例强行分到概率大的那一类去。
图示5.2:
图5.2(a)示意特征空间的一个划分。大正方形表示特征空间,被若干个小矩形分割,每个小矩形表示一个单元。所有单元构成一个集合, X X X 取值为单元的集合。图 5.2(b)中条件概率分布对应于图5.2(a)的划分.当某个单元 c c c 的条件概率满
足 P ( Y = + 1 ∣ X = c ) > 0.5 P(Y=+1|X=c)>0.5 P(Y=+1∣X=c)>0.5 时,则认为该单元属于正类,落在该单元的实例都视为正类。
决策树学习
过程描述:递归地选择最优特征,对训练数据进行分割,使得各子数据集有一个最好的分类。
- 首先,构建根结点,选最优特征,将数据集划分为子集
- 若子集已经被正确分类,则构建叶结点,将子集分到对应叶结点去
- 还有子集不能被正确分类,对这些子集选择新的最优特征,继续分割
- 直至:所有训练数据子集被正确分类;没有合适的特征
图示4.2:
3种递归返回:
- 当前结点包含的样本全属于同一类别,无需划分。
- 当前属性集为空,或所有样本在该属性上取值相同,无法划分。把当前结点标记为叶结点,将其类别设定为所含样本最多的类别。利用当前结点的后验分布。
- 当前结点包含的样本集合为空,不能划分。把当前结点标记为叶结点,将其类别设定为父结点所含样本最多的类别。把父结点的样本分布作为当前结点的先验分布。
4.2 划分(特征)选择
决策树的关键:如何选择最优划分属性。随着划分过程的不断进行,希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的“纯度”(purity)越来越高。
选取对训练数据具有分类能力的特征:按照这一特征将训练数据集分割成子集,使各子集在当前条件下有最好的分类。
4.2.1 信息增益
信息熵(information entropy):度量样本集合纯度。
当前样本集合: D D D,类别: k ∈ { 1 , 2 , ⋯ , ∣ Y ∣ } k \in \{1,2,\cdots,|\mathcal{Y}|\} k∈{1,2,⋯,∣Y∣},第 k k k类样本所占的比例: p k p_k pk
D D D的信息熵:
E n t ( D ) = − ∑ k = 1 ∣ Y ∣ p k ⋅ l o g 2 ( p k ) (4.1) \mathrm{Ent}(D) = -\sum_{k=1}^{|\mathcal{Y}|}p_k \cdot \mathrm{log}_2(p_k) \tag{4.1} Ent(D)=−k=1∑∣Y∣pk⋅log2(pk)(4.1)
E n t ( D ) \mathrm{Ent}(D) Ent(D) 的值越小, D D D 的纯度越高。熵越大,随机变量的不确定性越高。
条件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X):在已知随机变量 X X X 条件下随机变量 Y Y Y 的不确定性。
H ( Y ∣ X ) = ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y|X) = \sum_{i=1}^{n}p_iH(Y|X=x_i) H(Y∣X)=i=1∑npiH(Y∣X=xi)
离散属性: a = { a 1 , a 2 , ⋯ , a V } a = \{a^1, a^2, \cdots, a^V\} a={a1,a2,⋯,aV};使用 a a a 对样本集 D D D 进行划分,产生 V V V 个分支点。第 v v v 个分支点包含 D D D 中所有在属性 a a a 上取值为 a v a^v av 的样本,记为 D v D^v Dv。
根据式4.1计算出 D v D^v Dv 的信息熵,不同的分支结点包含样本数不同,给分支结点赋予权重 ∣ D v ∣ / ∣ D ∣ |D^v|/|D| ∣Dv∣/∣D∣,样本数越多的分支结点的影响越大,然后计算用属性 a a a 对样本集 D D D 进行划分后获得的 信息增益(information gain)
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) (4.2) \mathrm{Gain}(D, a) = \mathrm{Ent}(D) - \sum_{v=1}^{V} \frac{|D^v|}{|D|} \mathrm{Ent}(D^v) \tag{4.2} Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)(4.2)
注:式4.2 中的第二项就是条件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X)。信息增益表示得知特征 X X X 的信息而使得类 Y Y Y 的信息不确定性减少的程度,也是互信息(mutual information)
信息增益越大,意味着使用属性 a a a 进行划分所获得的纯度提升越大。
ID3算法:图4.2中算法第8行选择属性 a ∗ = arg max a ∈ A G a i n ( D , a ) a_* = \argmax_{a \in A} \mathrm{Gain}(D, a) a∗=argmaxa∈AGain(D,a)。
ID3 中的 ID:Iterative Dichotomiser(迭代二分器)。
ID3 算法:
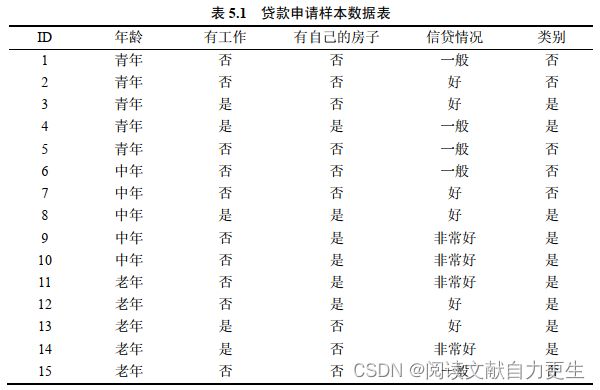
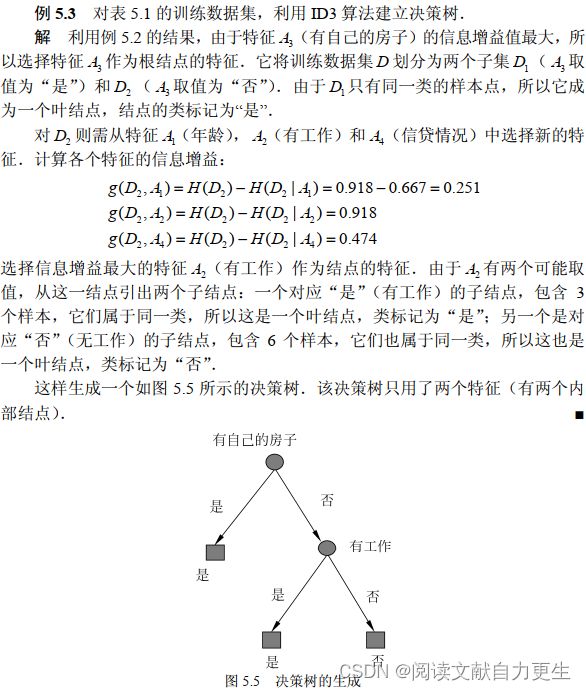
李书示例
表5.1:
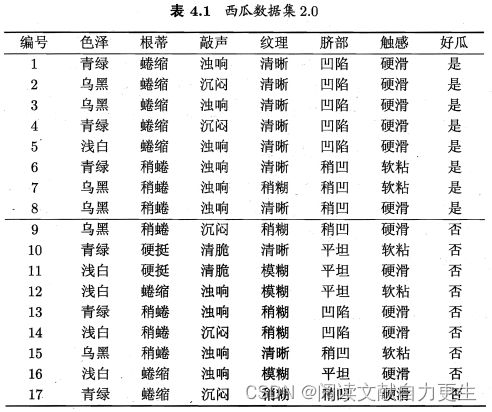
周书示例
表4.1:
4.2.2 增益率
在节4.2.1的划分过程中,若将 “编号” 引入划分属性中,则将产生 17 个分支,每个分支结点仅包含一个样本,这些分支结点的纯度已经最大。这会导致其信息增益远大于其他侯选属性。这样的决策树不具有泛化能力,无法对新样本进行预测。
信息增益准则对可取值数目较多的属性有所偏好。
C4.5决策树算法:使用**增益率(gain ratio)**来选择最优化分属性。
增益率定义:
G a i n _ r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) (4.3) \mathrm{Gain\_ratio}(D,a) = \frac{\mathrm{Gain}(D,a)}{\mathrm{IV}(a)} \tag{4.3} Gain_ratio(D,a)=IV(a)Gain(D,a)(4.3)
I V ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ (4.4) \mathrm{IV}(a) = -\sum_{v=1}^{V} \frac{|D^v|}{|D|} \mathrm{log}_2 \frac{|D^v|}{|D|} \tag{4.4} IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣(4.4)
I V ( a ) \mathrm{IV}(a) IV(a) 为属性 a a a 的固有值(intrinsic value)。属性 a a a 的可能取值数目越多(V越大),则 I V ( a ) \mathrm{IV}(a) IV(a) 的取值通常会越大。
但是,增益率准则对可取值数目较少的属性有所偏好。因此,C4.5决策树算法使用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
4.2.3 基尼指数
CART 决策树(Classification and Regression Tree):使用基尼指数来选择划分属性。
数据集 D D D 的纯度采用基尼值来度量:
G i n i ( D ) = ∑ k = 1 ∣ Y ∣ ∑ k ′ ≠ k p k p k ′ = 1 − ∑ k = 1 ∣ Y ∣ p k 2 (4.5) \mathrm{Gini}(D) = \sum_{k=1}^{|\mathcal{Y}|}\sum_{k'\neq k} p_k p_{k'}\\ =1 - \sum_{k=1}^{|\mathcal{Y}|}p_k^2 \tag{4.5} Gini(D)=k=1∑∣Y∣k′=k∑pkpk′=1−k=1∑∣Y∣pk2(4.5)
G i n i ( D ) \mathrm{Gini}(D) Gini(D):从数据集 D D D 中随机抽取两个样本,其类别标记不一致的概率。 G i n i ( D ) \mathrm{Gini}(D) Gini(D) 越小, D D D 的纯度越高。
则,属性 a a a 的基尼指数为:
G i n i _ i n d e x ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ G i n i ( D v ) (4.6) \mathrm{Gini\_index}(D,a) = \sum_{v=1}^{V} \frac{|D^v|}{|D|} \mathrm{Gini}(D^v) \tag{4.6} Gini_index(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)(4.6)
选择使得划分后基尼指数最小的属性作为最优化分属性,即 a ∗ = arg max a ∈ A G i n i _ i n d e x ( D , a ) a_* = \argmax_{a \in A} \mathrm{Gini\_index}(D, a) a∗=argmaxa∈AGini_index(D,a)
4.3 剪枝处理
决策树学习时,为尽可能正确分类训练样本,不断重复结点划分过程,造成决策树分支过多,容易导致把训练集自身的某些特点当成所有数据的一般性质——过拟合。
通过主动去掉一些分支来降低过拟合的风险。
两种剪枝策略:“预剪枝(prepruning)” 和 “后剪枝(postpurning)”。
采用留出法判断决策树的泛化性能:预留一部分训练数据作为“验证集”以进行性能评估。
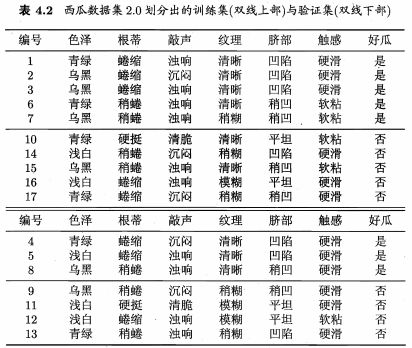
如对表4.1中数据集随机划分为两部分,表4.2:
从表4.2中训练集构建决策树,并分别研究剪枝方案。
4.3.1 预剪枝
决策树生成过程中,对每个结点在划分前先进行估计,若当前结点划分不能带来决策树泛化能力的提升,停止划分并将当前结点标记为叶结点。
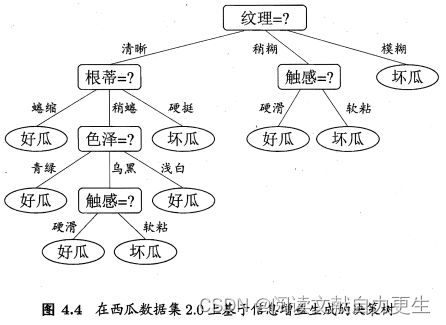
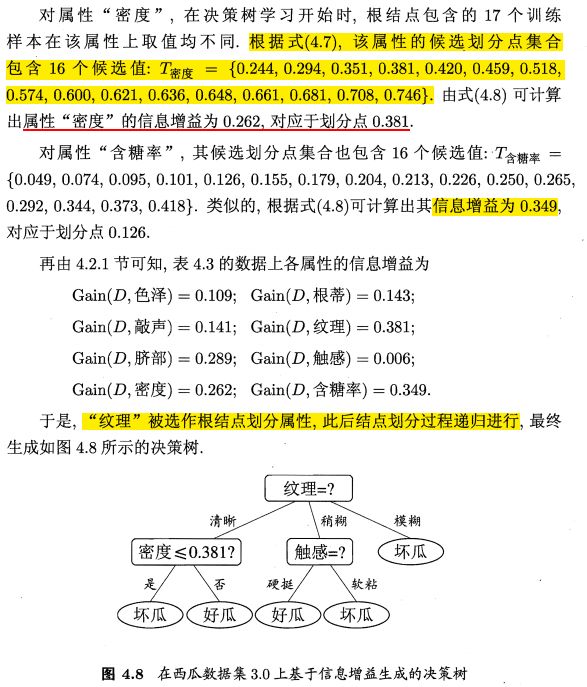
首先,根据信息增益准则,选取属性 脐部 对训练集划分,产生3个分支。
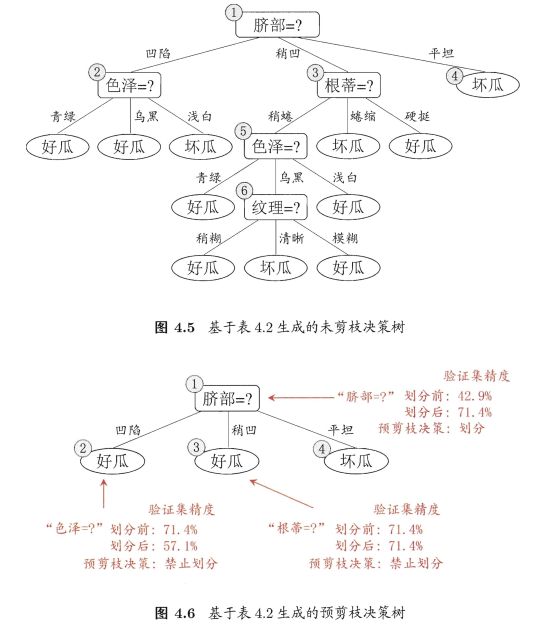
图4.5、4.6:
- 若不划分,样例都集中在根结点,根结点为叶结点,类别标记为训练样例数最多的类别——好瓜。
用表4.2验证集进行评估,编号 { 4 , 5 , 8 } \{4,5,8\} {4,5,8}分类正确。验证集精度: 3 7 × 100 % = 42.9 % \frac{3}{7} \times 100\%=42.9\% 73×100%=42.9% - 用属性
脐带划分后,验证集中 { 4 , 5 , 8 , 11 , 12 } \{4,5,8,11,12\} {4,5,8,11,12}分类正确,精度: 5 7 × 100 % = 71.4 % > 42.9 % \frac{5}{7} \times 100\%=71.4\%>42.9\% 75×100%=71.4%>42.9% - 因此,确定以
脐带进行划分
接下来分别对划分后各结点进行类似操作:
- 结点②:信息增益准则挑选
色泽为划分属性,划分后,编号 { 5 } \{5\} {5} 分类由正确转为错误,精度下降,预剪枝策略禁止结点②被划分。 - 结点③:最优属性
根蒂,划分后不能提升精度,不划分。 - 结点④:所含训练样本属于同一类,不再进行划分。
对比图4.5与图4.6:
- 预剪枝使决策树的很多分支没有展开,降低了过拟合的风险,减少了决策树的训练时间开销和测试时间开销
- 有些分支的当前划分虽不能提升泛化性能、甚至可能导致泛化性能暂时下降,但在其基础上进行的后续划分却有可能导致性能显著提高;预剪枝基于“ 贪心” 本质禁止这些分支展开,预剪枝决策树存在欠拟合风险
4.3.2 后剪枝
先从训练集生成完整决策树,然后自底向上对非叶结点进行考察,若将该结点对应子树替换为叶结点可提升泛化性能,则将该子树替换为叶结点。
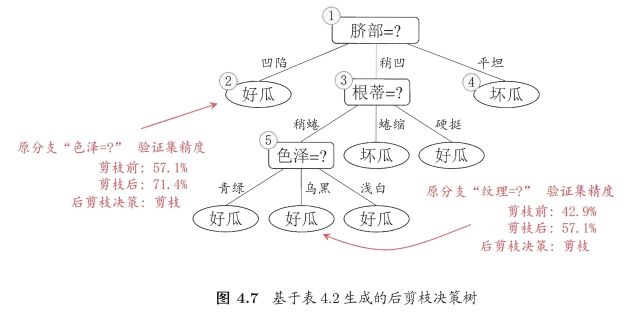
- 首先,考察图4.5中的结点⑥:若剪去其领衔分支,替换成叶结点。则,替换后叶结点包含 { 7 , 15 } \{7,15\} {7,15} 的训练样本,类别为 “好瓜”。验证集精度提高至 57.1 % 57.1\% 57.1%。后剪枝决定剪枝。
- 考察结点⑤:类似操作后,精度仍为 57.1 % 57.1\% 57.1%。不剪枝。
- 对结点②:提升至 71.4 % 71.4\% 71.4%.剪枝。
- 结点③和①:未得到提高,保留。
图4.7:
对比图 4.7 和图 4.6:
- 后剪枝一般比预剪枝保留更多分支
- 后剪枝欠拟合风险小,泛化能力往往优于预剪枝决策树
- 后剪枝在决策树完全生成后进行,且自底向上对树中所有非叶结点进行逐一考察,故训练时间开销比未剪枝决策树和预剪枝大很多
4.4 连续与缺失值
4.4.1 连续值处理
连续属性的可取值数目不再有限,不能直接根据连续属性的可取值来对结点进行划分——连续属性离散化:二分法。
样本集 D D D,连续属性 a a a,假定 a a a 在 D D D 上出现了 n n n 个不同的取值,从小到大排序: { a 1 , a 2 , ⋯ , a n } \{a^1,a^2,\cdots,a^n\} {a1,a2,⋯,an}。基于划分点 t t t 将 D D D 分为子集 D t − D_t^- Dt− 和 D t + D_t^+ Dt+, D t − D_t^- Dt− 包含在属性 a a a 上取值不大于 t t t 的样本, D t + D_t^+ Dt+ 包含在属性 a a a 上取值大于 t t t 的样本。
对相邻的属性取值 a i a^i ai 和 a i + 1 a^{i+1} ai+1, t t t 在区间 [ a i , a i + 1 ) [a^i,a^{i+1}) [ai,ai+1) 中取任意值所产生的划分结果相同。因此,对连续属性 a a a,考察包含 n − 1 n-1 n−1 个元素的候选划分点集合:
T a = { a i + a i + 1 2 ∣ 1 ≤ i ≤ n − 1 } (4.7) T_a = \{ \frac{a^i+a^{i+1}}{2} | 1 \leq i \leq n-1 \} \tag{4.7} Ta={2ai+ai+1∣1≤i≤n−1}(4.7)
即取区间 [ a i , a i + 1 ) [a^i,a^{i+1}) [ai,ai+1) 的中位点为候选划分点。然后,像离散属性值一样考察这些划分点,选取最优划分点进行样本集合划分。
式4.8:
G a i n ( D , a , t ) \mathrm{Gain}(D, a, t) Gain(D,a,t) 是样本集 D D D 基于划分点 t t t 二分后的信息增益。选择使 G a i n ( D , a , t ) \mathrm{Gain}(D, a, t) Gain(D,a,t) 最大化的二分点。
例子
表4.3:
注:与离散属性不同,若当前结点划分属性为连续属性,该属性还作为其后代结点的划分属性。例如在父结点上使用了 “密度≤0.381” , 不会禁止在子结点上使用 “密度≤0.294”。
4.4.2 缺失值处理
表4.4:
确定划分属性
样本集 D D D,属性 a a a, D ~ \tilde{D} D~ 表示 D D D 中在属性 a a a 上没有缺失值的样本子集。
根据 D ~ \tilde{D} D~ 来判断属性 a a a 的优劣。
假定:属性 a a a 有 V V V 个可取值 { a 1 , a 2 , ⋯ , a V } \{a^1,a^2,\cdots,a^V\} {a1,a2,⋯,aV}, D ~ v \tilde{D}^v D~v 表示 D ~ \tilde{D} D~ 中在属性 a a a 上取值为 a v a^v av 的样本子集, D ~ k \tilde{D}_k D~k 表示 D ~ \tilde{D} D~ 中属于第 k k k 类( k = 1 , 2 , ⋯ , ∣ Y ∣ k=1,2,\cdots,|\mathcal{Y}| k=1,2,⋯,∣Y∣)的样本子集。
有: D ~ = ⋃ k = 1 ∣ Y ∣ D ~ k = ⋃ v = 1 V D ~ v \tilde{D} = \bigcup_{k=1}^{|\mathcal{Y}|}\tilde{D}_k = \bigcup_{v=1}^{V}\tilde{D}^v D~=⋃k=1∣Y∣D~k=⋃v=1VD~v
为每个样本 x x x 赋予一个权重 w x w_x wx,
定义:
对属性 a a a:
- ρ ρ ρ 表示无缺值样本所占比例
- p ~ k \tilde{p}_k p~k 表示无缺失值样本中第 k k k 类所占比例
- r ~ v \tilde{r}_v r~v 表示无缺失值样本中属性 a a a 上取值 a v a^v av 的样本所占比例
信息增益计算推广式:
操作
对样本 x x x
- 若其在划分属性 a a a 上取值已知,将 x x x 划入与其取值对应的子结点,样本权值在子结点中保持为 w x w_x wx
- 若其在划分属性 a a a 上取值未知,将 x x x 划入所有子结点,样本权值在与属性值 a v a^v av 对应的子结点中调整为 r ~ v ⋅ w x \tilde{r}_v \cdot w_x r~v⋅wx。即:让同一个样本以不同的概率划入到不同的子结点中去
例子
以表4.4数据为例
4.5 多变量决策树
若视每个属性为坐标空间的一个坐标轴,则 d d d 个属性 描述的样本对应了 d d d 维空间中的一个数据点。
样本分类 ⟺ \iff ⟺ 在坐标空间中寻找不同类样本之间的分类边界。
决策树形成的分类边界:由若干个与坐标轴平行的分段组成。
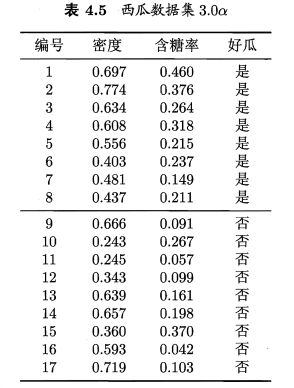
表4.5数据集构成的分类边界:
分类边界的每一段都与坐标轴平行,即每一段的划分都直接对应了某个属性的取值 ⇏ \nRightarrow ⇏ 当学习任务的真实分类边界比较复杂时。必须使用很多段划分才能获得较好的近似。
决策树会非常复杂:
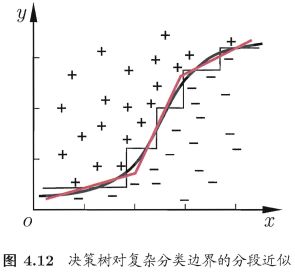
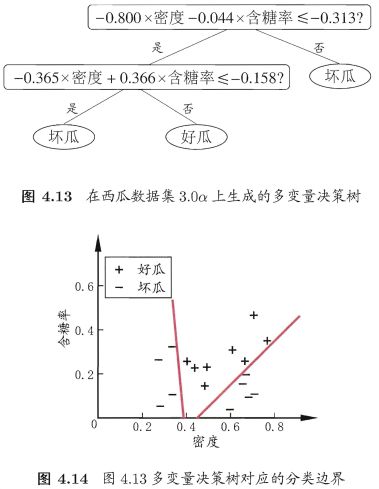
多变量决策树试图实现如图4.12中斜的划分边界,简化决策树模型。非叶结点不再是仅对某种属性,而是对属性的线性组合进行测试,即每个非叶结点是一个形如 ∑ i = 1 d w i a i = t \sum_{i=1}^{d}w_ia_i=t ∑i=1dwiai=t 的线性分类器。 w i w_i wi 为属性 a i a_i ai 的权重, w i w_i wi 和 t t t 可在该结点包含的样本集和属性集上学得。
多变量决策树在学习过程中试图建立合适的线性分类器。
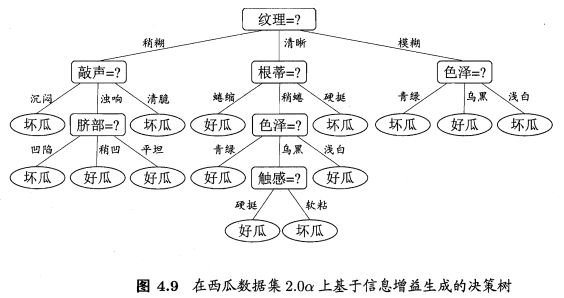
对数据集 3.0 α 3.0\alpha 3.0α
4.6 CART 算法
在给定输入随机变量 X X X 条件下输出随机变量 Y Y Y 的条件概率分布的学习方法。
CART 决策树
- 二叉树
- 内部结点特征的取值为 “是” 和 “否”,左分支为取值 “是” 的分支,右分支为取值 “否” 的分支
- 递归地二分每个特征,将输入空间即特征空间划分为有限个单元,在这些单元上确定预测的概率分布,即在输入给定的条件上输出的条件概率分布
CART 算法
- 决策树生成:基于训练数据集生成决策树,生成的决策树要尽量大
- 决策树剪枝:用验证数据集对已生成的树进行剪枝并选择最优子树,这时用损失函数最小作为剪枝的标准
4.6.1 CART 生成
对回归树用平方误差最小化准则,对分类树用基尼指数(Gini index)最小化准则,进行特征选择,生成二叉树。
1. 回归树生成
2. 分类树生成
基尼指数:分类问题,设有 K K K 个类,样本属于第 k k k 类的概率 p k p_k pk,概率分布的基尼指数定义为:
G i n i ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 (5.22) \mathrm{Gini}(p) = \sum_{k=1}^{K}p_k(1-p_k) = 1 - \sum_{k=1}^{K}p_k^2 \tag{5.22} Gini(p)=k=1∑Kpk(1−pk)=1−k=1∑Kpk2(5.22)
对于二类分类问题,若样本点属于第一类的概率为 p p p,则概率分布的基尼指数: G i n i ( p ) = 2 p ( 1 − p ) \mathrm{Gini}(p)=2p(1-p) Gini(p)=2p(1−p)。
样本集合 D D D,基尼指数为:
G i n i ( D ) = 1 − ∑ k = 1 K ( C k D ) 2 (5.24) \mathrm{Gini}(D) = 1 - \sum_{k=1}^{K}(\frac{C_k}{D})^2 \tag{5.24} Gini(D)=1−k=1∑K(DCk)2(5.24)
C k C_k Ck 是 D D D 中属于第 k k k 类的样本子集, K K K 是类的个数。
样本集合 D D D 根据特征 A A A 是否取某一可能值 a a a 被分割成 D 1 D_1 D1 和 D 2 D_2 D2 两部分:
D 1 = { ( x , y ) ∈ D ∣ A ( x ) = a } , D 2 = D − D 1 D_1=\{(x,y)\in D|A(x)=a\}, \quad D_2 = D - D_1 D1={(x,y)∈D∣A(x)=a},D2=D−D1
在特征 A A A 的条件下,集合 D D D 的基尼指数为:
G i n i ( D , A ) = D 1 D G i n i ( D 1 ) + D 2 D G i n i ( D 2 ) (5.25) \mathrm{Gini}(D,A) = \frac{D_1}{D} \mathrm{Gini}(D_1) + \frac{D_2}{D} \mathrm{Gini}(D_2) \tag{5.25} Gini(D,A)=DD1Gini(D1)+DD2Gini(D2)(5.25)
基尼指数表示集合 D D D 的不确定性, G i n i ( D , A ) \mathrm{Gini}(D,A) Gini(D,A) 表示经 A = a A=a A=a 分割后集合 D D D 的不确定性,基尼指数越大,样本集合的不确定性越大。
4.6.2 CART 剪枝
代码实现
在DNA数据集上通过ID3算法实现数据分类。