tensorflow入门——BP神经网络非线性回归最完整过程(含预测)
这是吐槽:
本科土木,由于各种经验公式的困扰,突发奇想想用神经网络去训练非线性的数据。然后从网络上查找资料,发现BP神经网络对非线性数据有良好的处理效果。从百度上copy的一句话:其突出优点就是具有很强的非线性映射能力和柔性的网络结构。 总之比人工猜测用公式回归会强很多,如果有同学跟我一样的情况也可以尝试这种非线性回归。对神经网络入门困难的同学,这个也是比mnist手写数字识别更为基础的教程。
由于非计算机专业,然后网上的教程并不是特别详细,有的有过程没有预测的步骤,有的有步骤没有预测方法,有的有预测又是简单的线性回归(线性回归我为啥不直接用最小二乘法?),一路上基本吧能趟的坑都趟完了T_T。所以下面就是我的趟坑实录,不。。。。tensorflow入门——BP神经网络非线性回归最完整过程。
1.安装环境
我的安装环境是win10 + Aanacoda(最新版)+python3.6(tf目前不兼容3.7)+tensorflow-gpu(最新版)+CUDA9.0+cudnn-9.0-windows10-x64-v7.3.1.20
显卡型号:GTX1050(tf只支持N卡,不支持A卡)
注:CUDA和cuDNN版本根据自己显卡选择,如果都不成功而且显卡跟我的差不多可以尝试我的搭配,安装Aanacoda还是很有必要的,不会让你的python版本和三方库混乱,在安装tensorflow和其他三方库时不要用Aanacoda的导航栏去安装,它只会安装最低版本(反正这样安装我是启动不了),选择终端打开环境,用pip安装最准确(不过需要提前配置好Aanacoda的源),如果以上方法都不起作用,请使用tensorflow—cpu版本吧,只是运算慢一点,对没有上万数据的非线性回归,训练时间应该是可以忍受的。
刚入门的同学也许就常常卡在环境配置这块,不用灰心,我当初啥也都不懂,对入门来说配置环境就是最大的一道难关,我也卡在这里,一个下午配置了五六次。上面并没有把环境配置说的很详细是因为网上资料其实很多,耐心去找一个个试一般都可以成功的。
2.人工神经网络介绍
人工神经网络近年大火,万恶的资本家的炒作给它加上了一种无所不能的光环。但是从最最基础的来源来说,其实就是我们小学学过的y=kx+b,神经网络里一般是写为y = wx+b。当然神经网络是由数个y = wx+b组成再结合一些信息论(loss函数)概率论,激活函数,等等一些数学方法。但是它的核心还是数个y=wx+b,所以人工神经网络并不是多复杂的东西,咱们小学就学过它最核心的东西。当然只是说理解和使用不会让你构成障碍,但是你要你从y = wx +b推导到神经网络甚至优化改进还是需要大量的知识储备的。
总之,使用tf学习框架的门槛并没有很高,一般上过小学有点相关基础的大学生都可以做到的。
知识背景:
(1)能看懂python代码:除了基础的语句用法(比如列表字典这些),还包括一些常用的三方库如numpy,matplotlib库等等,其实不懂也可以百度。
(2)数学基础:如矩阵相乘,正态分布(正态分布其实很有意思,运气就像一个自然规律一样,却可以用公式表达,学会了你可以科学算命,可以自行百度一下)
(3)能看懂我上面说的神经网络介绍。
好的步入正题:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
导入用到的模块
learning_rate = 0.05 #学习率
num_of_trian = 600 #训练的次数
training_display = 10 #每训练多少次显示
data_path = "data/model"#模型存放路径
一些初始参数的设置,大家可以尝试修改这些数据,观察对模型训练的影响
#生成添加噪音数据
x_data = np.linspace(-2,2,400)[:,np.newaxis]
noise = np.random.normal(0,0.5,x_data.shape)
y_data = np.square(x_data) - 0.5 + noise
生成带噪音的数据
#未添加噪点函数
x= np.linspace(-2,2,400)
y= np.square(x) - 0.5
这是原型曲线
#输入层
with tf.name_scope("inputs"):
xs = tf.placeholder(tf.float32,[None,1],name="x_input")
ys = tf.placeholder(tf.float32,[None,1],name="y_input")
这是输入层,xs,ys并不是数据,它只是一个占位符,就和图书馆占座一样,虽然有数,不过没人坐,是等着有人来坐。(tf.name_scope()是为了方便你在tensorboard生成一个图)
with tf.name_scope('hidden_layer'): #隐藏层。将隐藏层权重、偏置、净输入放在一起
with tf.name_scope('weight'): #权重
W1 = tf.Variable(tf.random_normal([1,10]))#一行十列随机正态分布。即十个神经元
tf.summary.histogram('hidden_layer/weight', W1)
with tf.name_scope('bias'): #偏置
b1 = tf.Variable(tf.zeros([1,10]))+0.1
tf.summary.histogram('hidden_layer/bias', b1)
with tf.name_scope('Wx_plus_b'): #净输入
Wx_plus_b1 = tf.matmul(xs,W1) + b1
tf.summary.histogram('hidden_layer/Wx_plus_b',Wx_plus_b1)
output1 = tf.nn.softplus(Wx_plus_b1) #激活函数relu平滑版
这里终于出现了我们所学的小学知识。w1就是小学公式中的k,b1就是b, Wx_plus_b1就是y了。
不过这里的w1并不是一个数,tf.random_normal([1,10]),生成了一个一行十列随机正态分布的矩阵,意思就是w1是一个由10个正态分布的w组成的矩阵。对应的tf.zeros([1,10])生成了一个一行十列的0矩阵,就是b1是一个由10个0组成的矩阵,加的0.1其实是初始的b,最佳的位置就是一条直线穿过所有的点,正好把所有的点分成两部分,线上方的点正好等于线下面的点的数量。不没到最佳位置也无所谓,大概的位置,对训练影响不大。
tf.matmul(xs,W1) 就是对应的元素相乘,不是矩阵相乘。
到这里就是完整的y = wx+b公式,再加上激活函数(大家也可以查找资料,激活函数并不复杂,网上 资料很多,这里不多介绍)。这也就是隐藏层的结构。
with tf.name_scope('output_layer'): #输出层。将输出层权重、偏置、净输入放在一起
with tf.name_scope('weight'): #权重
W2 = tf.Variable(tf.random_normal([10,1]))
tf.summary.histogram('output_layer/weight', W2)
with tf.name_scope('bias'): #偏置
b2 = tf.Variable(tf.zeros([1,1]))+0.1
tf.summary.histogram('output_layer/bias', b2)
with tf.name_scope('Wx_plus_b'): #净输入
Wx_plus_b2 = tf.matmul(output1,W2) + b2
tf.summary.histogram('output_layer/Wx_plus_b',Wx_plus_b2)
output2 = Wx_plus_b2
这个是输出层,大同小异,不过输出层一般没有激活函数。
#损失
with tf.name_scope("loss"):
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - output2),reduction_indices=[1]))
tf.summary.scalar("loss",loss)
损失函数,这个不明白也没有关系,其实就是求方差。。和最小二乘法有点像
with tf.name_scope("train"):
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
#合并数据
merged = tf.summary.merge_all()
GradientDescentOptimizer就是梯度下降的英语。梯度下降,可以理解为使导数差下降的,多维矩阵版,minimize就是要使loss最小。
好了到此为止,神经网络已经搭建完毕。结构非常简单,输入-隐藏-输出,再加上设置loss函数,设置梯度下降方法。
可能现在还有点蒙,还是不太理解为啥y = wx + b可以组成神经网络。那是因为还没有数据输入,整个网络还是空的,还没有进行变化。就是那个占座的人还没坐下来,你肯定会觉得这人没素质,等你看到他上完厕所坐下来,才会知道他还掏出了手机在图书馆打游戏刷微博。
#设置绘图器
plt.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('训练过程')
ax.scatter(x_data,y_data,s=5,label ="训练数据")
plt.plot(x,y,c = "red",label = "曲线原型")
plt.show(block = False)
设置matplot绘图器
with tf.Session() as sess:
#初始化
init = tf.global_variables_initializer()
sess.run(init)
#读取原有模型继续训练
#saver = tf.train.Sav er()
#saver.restore(sess, "data/model")
#写入训练数据到logs文件夹下
writer = tf.summary.FileWriter("logs",sess.graph)
开启会话,初始化,做好准备工作。
for train in range(num_of_trian):
sess.run(train_step,feed_dict={xs:x_data,ys:y_data})
prediction_value = sess.run(output2, feed_dict={xs: x_data})
lines = ax.plot(x_data, prediction_value, c = "blue", lw=5,label ="预测曲线")#绘制训练过程
plt.legend()#显示标题元素
plt.pause(0.1)
if train % training_display == 0:
result = sess.run(merged,feed_dict={xs:x_data,ys:y_data})
writer.add_summary(result,train)
print(train,sess.run(loss,feed_dict={xs:x_data,ys:y_data}))
plt.savefig("picture\\"+str(train)+".png")#保存训练图片
try:
ax.lines.remove(lines[0])
except Exception:
pass
saver = tf.train.Saver()
saver.save(sess,data_path)#储存模型
这里就开始喂入数据了,通过sess.run()可以将数据在整个神经网络上跑。
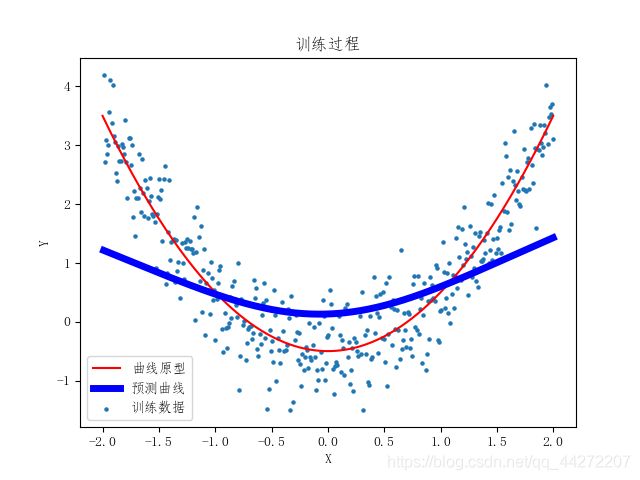
一开始xs数据先进入,通过y = wx +b 求出来y,ys数据再进去和算出来的y(即output)对比,他会告诉神经网络调整w,b,就好像xs位置上的人在打游戏,旁边ys位置上的人看到了说:“小老弟,你的技术(w)和手机配置(b)不行哦。”,xs位置上的小老弟听了觉得有道理,调整技术(w)提升了手机配置(b),这样就完成了一次训练过程。
第二次训练,还是xs位置上的人开始打游戏,ys上的人看了又说:“手机配置(b)可以了,技术还是要提升一点(w)。”,小老弟听了觉得有道理,不换手机(b)开始提升技术(w)。
当然,一般不会出现第二轮训练b就不变了,xs的水平取决与ys的水平。如果ys只是黄金,那么xs听取了千百次ys的建议。则xs的技术和手机配置就会越来越像ys
则他的水平就越来越像ys。
训练过程不难理解,可是为啥要10个w和b?就在于,我们回归的是非线性模型。在我们的隐藏层中有10个神经元,一个神经元对应一个w,b。每个神经元相当于记录了要学习的曲线一个特征。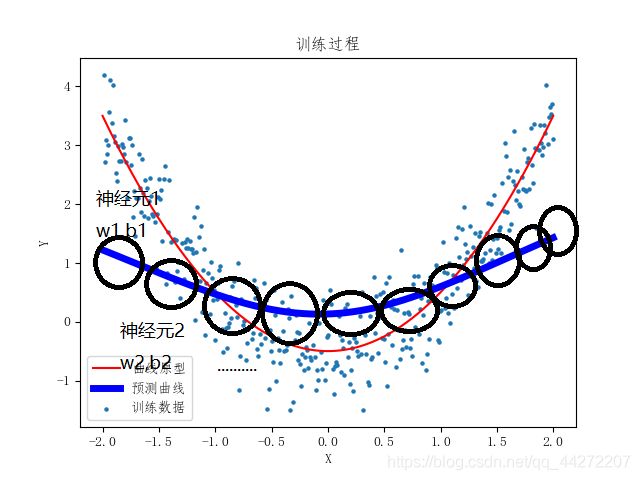
这是一个不恰当的例子,神经元的数字特征更为抽象,不过我们也可以知道,神经元越多,特征越多。同样的网络层数越多,收集的特征也越多。模型拟合的情况会越好,不过,它们的数量应当在一个合适的范围,否则会浪费计算资源。
#用于预测模型上任意一点
flag = True
with tf.Session() as sess2:
sess2.run(init)
saver = tf.train.Saver()
saver.restore(sess2, data_path)
while flag:
b = input("请输入读取的X值:")
if b == "exit":
flag = False
else:
a = eval("np.array([["+b+"]])")
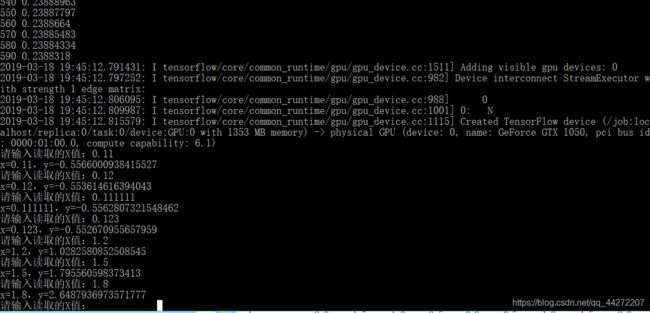
print ("x={},y={}".format(a[0][0], sess2.run(output2, feed_dict={xs:a})[0][0]))
最后一步,预测!终于,千百次训练下,xs上的小老弟觉得,他对ys的技术(w)和手机配置(b)都了然于心并且记在了小本本feed_dict{}上,不过这时feed_dict{}并不是用来储存,而是用来索引,根据xs对应的元素,找到对应的w和b,用sess2.run()把xs上的值(由你给出)从神经网络再跑一次。进行诸如xw + b的计算,得到结果。就完成了一次预测。
这个神经网络由于数据量较小,所以一开始是直接将所有数据都写进了x_data,y_data的矩阵,所以在喂数据时要注意它的形状,或者说格式
“np.array([["+b+"]])",总之就是训练怎么喂,预测也要怎么喂。
模型训练完成也可调用tensorboard在当前目录下查看训练数据
具体步骤:cd到代码所在目录—>输入tensorboard --logdir logs—>浏览器访问给出的浏览地址或是http://localhost:6006/即可看到高大上的图形界面啦

全文结束,神经网络的学习并不是我说的那么轻松,你可能要坐在电脑前一周,可能配置环境就要一天。我写的如此欢乐,只是苦中作乐罢了。不过用一两周的时间能入门现在最火的神经网络,或是掌握一个强大的非线性回归工具也是很不错的收获。
如果有收获的同学,请点个赞,或者在下方回复一下。如果有不对的地方,有大神看出来也请在下方留言指正。
以下是全代码
import tensorflow as tf
#import csv
import numpy as np
import matplotlib.pyplot as plt
learning_rate = 0.05 #学习率
num_of_trian = 100 #训练的次数
training_display = 10 #每训练多少次显示
data_path = "data/model"#模型存放路径
filename = "data/testdata.csv"#csv数据路径
#生成添加噪点数据
x_data = np.linspace(-2,2,400)[:,np.newaxis]
noise = np.random.normal(0,0.5,x_data.shape)
y_data = np.square(x_data) - 0.5 + noise
"""
x1,y1 = [],[]
#读取csv数据
with open(filename) as f:
reader = csv.reader(f)
header_row = next(reader)
for line in reader:
x1.append([eval(line[0])])
y1.append([eval(line[1])])
x_data = np.array(x1)
y_data = np.array(y1)"""
#未添加噪点函数
x= np.linspace(-2,2,400)
y= np.square(x) - 0.5
#输入层
with tf.name_scope("inputs"):
xs = tf.placeholder(tf.float32,[None,1],name="x_input")
ys = tf.placeholder(tf.float32,[None,1],name="y_input")
#隐藏层
with tf.name_scope('hidden_layer'): #隐层。将隐层权重、偏置、净输入放在一起
with tf.name_scope('weight'): #权重
W1 = tf.Variable(tf.random_normal([1,10]))#一行十列随机正态分布。即十个神经元
tf.summary.histogram('hidden_layer/weight', W1)
with tf.name_scope('bias'): #偏置
b1 = tf.Variable(tf.zeros([1,10]))+0.1
tf.summary.histogram('hidden_layer/bias', b1)
with tf.name_scope('Wx_plus_b'): #净输入
Wx_plus_b1 = tf.matmul(xs,W1) + b1
tf.summary.histogram('hidden_layer/Wx_plus_b',Wx_plus_b1)
output1 = tf.nn.softplus(Wx_plus_b1) #激活函数relu平滑版
#输出层
with tf.name_scope('output_layer'): #输出层。将输出层权重、偏置、净输入放在一起
with tf.name_scope('weight'): #权重
W2 = tf.Variable(tf.random_normal([10,1]))
tf.summary.histogram('output_layer/weight', W2)
with tf.name_scope('bias'): #偏置
b2 = tf.Variable(tf.zeros([1,1]))+0.1
tf.summary.histogram('output_layer/bias', b2)
with tf.name_scope('Wx_plus_b'): #净输入
Wx_plus_b2 = tf.matmul(output1,W2) + b2
tf.summary.histogram('output_layer/Wx_plus_b',Wx_plus_b2)
output2 = Wx_plus_b2
#损失
with tf.name_scope("loss"):
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - output2),reduction_indices=[1]))
tf.summary.scalar("loss",loss)
#训练过程 设置学习率配置损失函数
with tf.name_scope("train"):
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
#合并数据
merged = tf.summary.merge_all()
#设置绘图器
plt.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('训练过程')
ax.scatter(x_data,y_data,s=5,label ="训练数据")
plt.plot(x,y,c = "red",label = "曲线原型")
plt.show(block = False)
with tf.Session() as sess:
#初始化
init = tf.global_variables_initializer()
sess.run(init)
#读取原有模型继续训练
#saver = tf.train.Sav er()
#saver.restore(sess, "data/model")
#写入训练数据到logs文件夹下
writer = tf.summary.FileWriter("logs",sess.graph)
for train in range(num_of_trian):
sess.run(train_step,feed_dict={xs:x_data,ys:y_data})
prediction_value = sess.run(output2, feed_dict={xs: x_data})
lines = ax.plot(x_data, prediction_value, c = "blue", lw=5,label ="预测曲线")#绘制训练过程
plt.legend()#显示标题元素
plt.pause(0.1)
if train % training_display == 0:
result = sess.run(merged,feed_dict={xs:x_data,ys:y_data})
writer.add_summary(result,train)
print(train,sess.run(loss,feed_dict={xs:x_data,ys:y_data}))
plt.savefig("picture\\"+str(train)+".png")#保存训练图片
try:
ax.lines.remove(lines[0])
except Exception:
pass
saver = tf.train.Saver()
saver.save(sess,data_path)#储存模型
#用于预测模型上任意一点
flag = True
with tf.Session() as sess2:
sess2.run(init)
saver = tf.train.Saver()
saver.restore(sess2, data_path)
while flag:
b = input("请输入读取的X值:")
if b == "exit":
flag = False
else:
a = eval("np.array([["+b+"]])")
print ("x={},y={}".format(a[0][0], sess2.run(output2, feed_dict={xs:a})[0][0]))
